Имеется несколько семейств симметричных многогранников с неприводимой симметрией, которые имеют представителей более чем в одной размерности. В данной таблице семейства приведены с проекцией в виде графа Петри и с диаграммами Коксетера — Дынкина.
| Семейство n[en] |
n-симплекс | n-гиперкуб | n-ортоплекс | n-полукуб[en] | 1k2[en] | 2k1[en] | k21[en] | пятиугольный многогранник | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Группа | An | BCn |
|
|
Hn | |||||||||||
| 2 |  |
 |
 p-угольник (пример: p=7) |
 Шестиугольник |
 Пятиугольник | |||||||||||
| 3 |  Тетраэдр |
 Куб |
 Октаэдр |
 Тетраэдр |
 Додекаэдр |
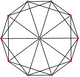 Икосаэдр | ||||||||||
| 4[en] |  Пятиячейник |
 |
 Шестнадцати- ячейник |
 |
 Двадцати- четырёхячейник |
 Стодвадцатиячейник |
 Шестисотячейник | |||||||||
| 5[en] |  Гексатерон |
 Пентеракт |
 5-ортоплекс |
 5-полукуб[en] |
||||||||||||
| 6[en] |  6-симплекс |
 6-куб |
 6-ортоплекс |
 6-полукуб[en] |
 122[en] |
 221[en] |
||||||||||
| 7[en] |  7-симплекс |
 7-куб[en] |
 7-ортоплекс[en] |
 7-полукуб[en] |
 132[en] |
 231[en] |
 321[en] |
|||||||||
| 8[en] |  8-симплекс |
 8-куб[en] |
 8-ортоплекс[en] |
 8-полукуб[en] |
 142[en] |
 241[en] |
 421[en] |
|||||||||
| 9[en] |  8-симплекс |
 9-куб[en] |
 9-ортоплекс[en] |
 9-полукуб[en] |
||||||||||||
| 10[en] |  10-симплекс |
 10-куб |
 10-ортоплекс[en] |
 10-полукуб[en] |
||||||||||||
Для улучшения этой статьи желательно: |
Данная страница на сайте WikiSort.ru содержит текст со страницы сайта "Википедия".
Если Вы хотите её отредактировать, то можете сделать это на странице редактирования в Википедии.
Если сделанные Вами правки не будут кем-нибудь удалены, то через несколько дней они появятся на сайте WikiSort.ru .