WikiSort.ru - Не сортированное

Дважды косо отсечённый икосаэдр
(3D-модель)
Тип	многогранник Джонсона
Свойства	выпуклый
Комбинаторика
Элементы	12 граней 20 рёбер 10 вершин
Грани	10 треугольников 2 пятиугольника
Конфигурация вершины	2(3.52) 2+4(33.5) 2(35)
Развёртка
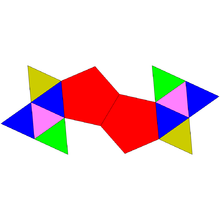Классификация
Обозначения	J62, М7+М3
Группа симметрии	C2v

Два́жды ко́со отсечённый икоса́эдр^[1] — один из многогранников Джонсона (J₆₂, по Залгаллеру — М₇+М₃).

Составлен из 12 граней: 10 правильных треугольников и 2 правильных пятиугольников. Каждая пятиугольная грань окружена пятиугольной и четырьмя треугольными; среди треугольных 2 грани окружены двумя пятиугольными и треугольной, 4 грани — пятиугольной и двумя треугольными, остальные 4 — тремя треугольными.

Имеет 20 рёбер одинаковой длины. 1 ребро располагается между двумя пятиугольными гранями, 8 рёбер — между пятиугольной и треугольной, остальные 11 — между двумя треугольными.

У дважды косо отсечённого икосаэдра 10 вершин. В 2 вершинах сходятся две пятиугольных грани и одна треугольная; в 6 вершинах сходятся одна пятиугольная грань и три треугольных; в остальных 2 — пять треугольных.

Дважды косо отсечённый икосаэдр можно получить из икосаэдра, отсекши от того две правильных пятиугольных пирамиды^[en] (J₂), основания которых имеют общее ребро. Вершины полученного многогранника — 10 из 12 вершин икосаэдра, рёбра — 20 из 30 рёбер икосаэдра; отсюда ясно, что у дважды косо отсечённого икосаэдра тоже существуют описанная и полувписанная сферы, причём они совпадают с описанной и полувписанной сферами исходного икосаэдра.

Метрические характеристики

Если дважды косо отсечённый икосаэдр имеет ребро длины ${\displaystyle a}$ , его площадь поверхности и объём выражаются как

${\displaystyle S={\frac {1}{2}}\left(5{\sqrt {3}}+{\sqrt {25+10{\sqrt {5}}}}\right)a^{2}\approx 7,7710818a^{2},}$

${\displaystyle V={\frac {1}{6}}\left(5+2{\sqrt {5}}\right)a^{3}\approx 1,5786893a^{3}.}$

Радиус описанной сферы (проходящей через все вершины многогранника) при этом будет равен

${\displaystyle R={\frac {1}{4}}{\sqrt {10+2{\sqrt {5}}}}\;a\approx 0,9510565a;}$

радиус полувписанной сферы (касающейся всех рёбер в их серединах) —

${\displaystyle \rho ={\frac {1}{4}}\left(1+{\sqrt {5}}\right)a\approx 0,8090170a.}$

Примечания

Ссылки

• Weisstein, Eric W. Дважды косо отсечённый икосаэдр (англ.) на сайте Wolfram MathWorld.