WikiSort.ru - Не сортированное

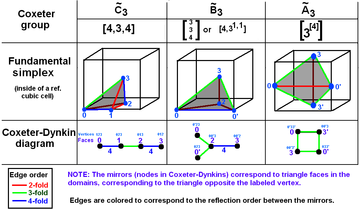
Диаграмма Коксетера — Дынкина (или диаграмма Коксетера, граф Коксетера, схема Коксетера^[1]) — это граф с помеченными числами рёбрами (называемыми ветвями), представляющими пространственные связи между набором зеркальных симметрий (или гиперплоскостей зеркальных отражений). Диаграмма описывает калейдоскопичное построение — каждая «вершина» графа представляет зеркало (грань фундаментальной области), а метки ветвей задают величину двугранного угла между двумя зеркалами (на гребне фундаментальной области, то есть на грани с размерностью $n-2$ ). Непомеченные ветви неявно подразумевают порядок 3.

Каждая диаграмма представляет группу Коксетера, и группы Коксетера классифицируются ассоциированными с ними диаграммами.

Диаграммы Дынкина тесно связаны с диаграммами Коксетера и отличаются от них в двух отношениях — во-первых, ветви с меткой «4» и выше являются ориентированными, в то время как в диаграммах Коксетера они неориентированные, во-вторых, диаграммы Дынкина должны удовлетворять дополнительному (кристаллографическому^[en]) ограничению, а именно, в качестве меток разрешены только 2, 3, 4 и 6. Диаграммы Дынкина соответствуют системе корней и используются для их классификации, а потому соответствуют полупростым группам Ли^[2].

Описание

Ветви диаграммы Коксетера — Дынкина помечаются рациональными числами p, соответствующими двугранным углам 180°/p. Если p = 2, угол равен 90° и зеркала никак не влияют друг на друга, так что ветвь может быть исключена из диаграммы. Если ветвь не помечена, предполагается, что p = 3, что соответствует углу 60°. Два параллельных зеркала имеют ветвь, помеченную знаком «∞». В принципе, n отражений могут быть представлены полным графом, в котором все n(n − 1) / 2 ветвей нарисованы. На практике, почти все интересные комбинации отражений содержат некоторое число прямых углов, так что соответствующие ветви могут быть исключены.

Диаграммы могут быть обозначены согласно их структуре графа. Первыми формами, которые изучал Людвиг Шлефли, были симплексы, определяемые набором взаимноперпендикулярных рёбер. Эти симплексы Шлефли назвал ортосхемами^[en]. Ортосхемы возникают в различных контекстах, а особенно при рассмотрении правильных политопов и правильных сотов^[en]. Плагиосхемы — это симплексы, представленные ветвящимися графами, а циклосхемы — симплексы, представленные циклическими графами.

Матрица Грама (Шлефли)

Любая диаграмма Коксетера имеет соответствующую матрицу Шлефли с элементами $a_{i,\;j}=a_{j,\;i}=-2\cos \left({\frac {\pi }{p}}\right)$ , где $p$ — порядок ветки между парами отражений. Как матрица косинусов, она также называется матрицей Грама по имени Ёргена Грама^[en]. Все матрицы Грама группы Коксетера симметричны, поскольку их корневые вектора нормализованы. Они близко связаны с матрицами Картана, которые используются в подобном контексте, но для ориентированных графов диаграмм Дынкина для случаев p = 2,3,4 и 6 и которые, в общем случае, НЕ симметричны.

Определитель матрицы Шлефли называется шлефианом (он же грамиан) и его знак определяет, является ли группа конечной (положительный определитель), аффинной (нулевой) или неопределённой (отрицательный). Это правило называется критерием Шлефли^[3].

Собственные значения матрицы Грама определяют, является ли группа Коксетера конечного типа (все значения положительны), аффинного типа (все неотрицательны, по меньшей мере одно значение равно нулю) или неопределённого типа (все остальные случаи). Неопределённый тип иногда далее разбивается на подтипы, например, на гиперболические и остальные группы Коксетера. Однако имеется много неэквивалентных определений гиперболических групп Коксетера. Мы используем следующее определение: Группа Коксетера с соответствующей диаграммой является гиперболической, если она ни конечного, ни аффинного типов, но любая связная поддиаграмма имеет либо конечный, либо аффинный тип. Гиперболическая группа Коксетера компактна, если все её подгруппы конечны (то есть имеют положительные определители) и паракомпактна, если все её подгруппы конечны или аффинны (то есть имеют неотрицательные определители)^[4].

Конечные и аффинные группы также называются эллиптическими и параболическими соответственно. Гиперболические группы называются также группами Ланнера (F. Lannér), который перечислил компактные гиперболические группы в 1950-м^[5], а паракомпактные группы — группами Козула (Koszul; или квазиланнеровыми группами). Встречаются и другие названия. Так, в статье Максвелла^[6] конечные группы называются положительными, а аффинные — евклидовыми.

Группы Коксетера ранга 2

Для ранга 2 тип группы Коксетера полностью определён определителем матрицы Грама, поскольку он просто равен произведению его собственных значений: конечный тип (положительный определитель), аффинный тип (нулевой определитель) или гиперболический тип (отрицательный определитель). Коксетер использует эквивалентную скобочную нотацию^[en], которая перечисляет последовательности порядков веток вместо графических диаграмм узел-ветвь.

Тип	Конечная					Аффинная	Гиперболическая
Геометрия					…
Коксетер	[ ]	[2]	[3]	[4]	[p]	[∞]	[∞]	[iπ/λ]
порядок	2	4	6	8	2p	∞
Прямые отражения раскрашены соответственно узлам диаграммы Коксетера. Фундаментальные области выкрашены в альтернативные цвета.

Диаграммы группы Коксетера ранга 2
Порядок p	Группа	Диаграмма Коксетера		Матрица Грама
Порядок p	Группа	Диаграмма Коксетера		$\left[{\begin{matrix}2&a_{12}\\a_{21}&2\end{matrix}}\right]$	Определитель (4-a₂₁*a₁₂)
Конечная (Определитель>0)
2	I₂(2) = A₁xA₁		[2]	$\left[{\begin{smallmatrix}2&0\\0&2\end{smallmatrix}}\right]$	4
3	I₂(3) = A₂		[3]	$\left[{\begin{smallmatrix}2&-1\\-1&2\end{smallmatrix}}\right]$	3
4	I₂(4) = B₂		[4]	$\left[{\begin{smallmatrix}2&-{\sqrt {2}}\\-{\sqrt {2}}&2\end{smallmatrix}}\right]$	2
5	I₂(5) = H₂		[5]	$\left[{\begin{smallmatrix}2&-\phi \\-\phi &2\end{smallmatrix}}\right]$	$4\sin ^{2}(\pi /5)$ = $(5-{\sqrt {5}})/2$ ~1.38196601125
6	I₂(6) = G₂		[6]	$\left[{\begin{smallmatrix}2&-{\sqrt {3}}\\-{\sqrt {3}}&2\end{smallmatrix}}\right]$	1
8	I₂(8)		[8]	$\left[{\begin{smallmatrix}2&-2\cos(\pi /8)\\-2\cos(\pi /8)&2\end{smallmatrix}}\right]$	$2-{\sqrt {2}}$ ~0.58578643763
10	I₂(10)		[10]	$\left[{\begin{smallmatrix}2&-2\cos(\pi /10)\\-2\cos(\pi /10)&2\end{smallmatrix}}\right]$	$4\sin ^{2}(\pi /10)$ = $(3-{\sqrt {5}})/2$ ~0.38196601125
12	I₂(12)		[12]	$\left[{\begin{smallmatrix}2&-2\cos(\pi /12)\\-2\cos(\pi /12)&2\end{smallmatrix}}\right]$	$2-{\sqrt {3}}$ ~0.26794919243
p	I₂(p)		[p]	$\left[{\begin{smallmatrix}2&-2\cos(\pi /p)\\-2\cos(\pi /p)&2\end{smallmatrix}}\right]$	$4\sin ^{2}(\pi /p)$
Аффинная (Определитель=0)
∞	I₂(∞) = ${\tilde {I}}_{1}$ = ${\tilde {A}}_{1}$		[∞]	$\left[{\begin{smallmatrix}2&-2\\-2&2\end{smallmatrix}}\right]$	0
Гиперболическая (Определитель≤0)
∞			[∞]	$\left[{\begin{smallmatrix}2&-2\\-2&2\end{smallmatrix}}\right]$	0
∞			[iπ/λ]	$\left[{\begin{smallmatrix}2&-2cosh(2\lambda )\\-2cosh(2\lambda )&2\end{smallmatrix}}\right]$	$-4\sinh ^{2}(2\lambda )\leq 0$

Геометрическое представление

Диаграмму Коксетера — Дынкина можно рассматривать как графическое описание фундаментальной области отражений. Зеркалом (множеством неподвижных точек отражения) является гиперплоскость в заданном сферическом, евклидовом или гиперболическом пространстве. (В двумерном пространстве зеркалом служит прямая, а в трёхмерном — плоскость).

Ниже показаны фундаментальные области двумерных и трёхмерных евклидовых групп, а также двумерных сферических групп. Для каждой группы диаграмма Коксетера может быть выведена путём определения гиперплоскостей и разметки их связей, игнорируя при этом двугранные углы в 90 градусов (порядок 2).

Группа Коксетера	${\tilde {C}}_{2}$	${\tilde {I}}_{1}$ x ${\tilde {I}}_{1}$	${\tilde {G}}_{2}$	${\tilde {A}}_{2}$
Группа Коксетера	[4,4]	[∞4,∞]	[6,3]	[(3,3,3)] = [3^[3]]
Фундаментальная область
Диаграмма Коксетера — Дынкина

Группы Коксетера на евклидовой плоскости с соответствующими диаграммами. Зеркала помечены как узлы графа R1, R2, и т. д. и раскрашены соответственно порядку отражения. Отражения на 90 градусов ничего не меняют, а потому удалены из диаграммы. Параллельные отражения отмечены символом ∞. Призматическая группа ${\tilde {I}}_{1}$ x ${\tilde {I}}_{1}$ показана как удвоение ${\tilde {C}}_{2}$ , но она также может быть создана как прямоугольные области, полученные из удвоения треугольников ${\tilde {G}}_{2}$ . ${\tilde {A}}_{2}$ является удвоением треугольника ${\tilde {G}}_{2}$ .

Некоторые гиперболические калейдоскопы
Группа Коксетера	[n,4]	[∞n,∞]	[n,3]	[(n,3,3)]
Фундаментальная область
Двойственный граф (полная схема Коксетера)
Диаграмма Коксетера — Дынкина
	n=5,6...	n=3,4...	n=7,8...	n=4,5

Многие группы Коксетера на гиперболической плоскости могут быть распространены из евклидова случая как серии гиперболических решений.

Группы Коксетера в трёхмерном пространстве с соответствующими диаграммами. Зеркала (треугольные грани) помечены противоположными вершинами 0..3. Ветви выкрашены соответственно порядку отражений. ${\tilde {C}}_{3}$ заполняет 1/48 часть куба. ${\tilde {B}}_{3}$ заполняет 1/24 часть куба. ${\tilde {A}}_{3}$ заполняет 1/12 часть куба.	Группы Коксетера на сфере с соответствующими диаграммами. Одна фундаментальная область выделена жёлтым цветом. Вершины области (и ветви графа) выкрашены соответственно порядку отражения.

Конечные группы Коксетера

См. также семейства многогранников для таблицы однородных многогранников, связанных с этими группами.

Для каждой группы приведены три различных обозначения — буквенно-цифровое обозначение, набор цифр в скобках и диаграмма Коксетера.
Разветвлённые группы D_n являются половинными или знакопеременными версиями обычных групп C_n.
Для разветвлённых групп D_n и E_n приведены обозначения с верхними индексами [3^a,b,c], где числа a,b и c задают количество сегментов в каждой из трёх ветвей.

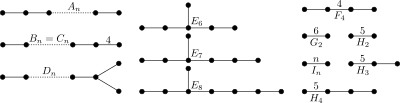
Связанные графы Дынкина с рангами от 1 до 9
Ранг	Простые группы Ли			Исключительные группы Ли
Ранг	${A}_{1+}$	${BC}_{2+}$	${D}_{2+}$	${E}_{3-8}$ ^[en]	${F}_{3-4}$	${G}_{2}$	${H}_{2-4}$	${I}_{2}(p)$
1	A₁=[]
2	A₂=[3]	B₂=[4]	D₂=A₁xA₁			G₂=[6]	H₂=[5]	I₂[p]
3	A₃=[3²]	B₃=[3,4]	D₃=A₃	E₃=A₂A₁	F₃=B₃		H₃
4	A₄=[3³]	B₄=[3²,4]	D₄=[3^1,1,1]	E₄=A₄	F₄		H₄
5	A₅=[3⁴]	B₅=[3³,4]	D₅=[3^2,1,1]	E₅=D₅
6	A₆=[3⁵]	B₆=[3⁴,4]	D₆=[3^3,1,1]	E₆=[3^2,2,1]
7	A₇=[3⁶]	B₇=[3⁵,4]	D₇=[3^4,1,1]	E₇=[3^3,2,1]
8	A₈=[3⁷]	B₈=[3⁶,4]	D₈=[3^5,1,1]	E₈=[3^4,2,1]
9	A₉=[3⁸]	B₉=[3⁷,4]	D₉=[3^6,1,1]
10+	..	..	..	..

Приложение для однородных политопов

Диаграммы Коксетера — Дынкина могут явно перечислить почти все классы однородных многогранников^[en] и однородных мозаик. Каждый однородный многогранник с простой зеркальной симметрией (все они, за исключением нескольких специальных случаев, имеют простую зеркальную симметрию) могут быть представлены диаграммами Коксетера — Дынкина с перестановками меток. Каждый однородный многогранник можно получить, используя такие зеркала и одну генерирующую точку — отражения создают в результате симметрии новые точки, затем можно определить рёбра многогранника между точками и их зеркальными отражениями. Грани можно построить при получении цикла из рёбер и т. д. Для задания генерирующей вершины один или более узлов помечаются кружками, что означает, что вершина не находится на зеркале(-ах), представленных помеченными кружками узлами. (Если два или более зеркала помечены, вершина располагается на равноудалённом расстоянии от них.) Зеркало активно (создаёт отражения), только для точек, не лежащих на нём. Диаграмма должна иметь по меньшей мере один активный узел для представления многогранника.

Все правильные многомерные многогранники, представленные символом Шлефли (p, q, r, …), могут иметь фундаментальные области, представленные набором n зеркал с соответствующей диаграммой Коксетера — Дынкина в виде последовательности узлов и ветвей, помеченных p, q, r, … с первым обведённым кружком узлом.

Однородные многогранники с одним кружком соответствуют генерирующим точкам в углах симплекса фундаментальной области. Два кружка соответствуют рёбрам симплекса и имеют свободу выбора, но только середина приводит к однородному решению с одинаковыми длинами рёбер. В общем случае генераторы с k-кружками являются (k-1)-мерными гранями симплекса. Если все узлы помечены кружками, генерирующая точка находится внутри симплекса.

Другой элемент разметки выражает специальный случай незеркальной симметрии однородных многогранников. Эти случаи существуют как альтернации^[en] зеркальной симметрии многогранников. В этом элементе разметки отсутствует центральная точка помеченного кружком узла, который тогда называется дыркой, и означает такой узел удалённую альтернирующую вершину. Полученный многогранник будет иметь подсимметрии исходной группы Коксетера. Усечённая альтернация называется обрезком^[en].

Отдельный узел представляет отдельное зеркало. Соответствующая группа обозначается A₁. Кружок вокруг узла приводит к образованию отрезка, перпендикулярного зеркалу, и он обозначается как {}.
Два несвязанных узла представляют два перпендикулярных зеркала. Если оба узла обведены кружком, может быть создан прямоугольник, или квадрат, если точки расположены на одинаковом расстоянии от обоих зеркал.
Два узла, соединённых ветвью порядка n, могут создать n-угольник, если точка находится на одном из зеркал, и 2n-угольник, если точка не лежит ни на одном из зеркал. Эти два узла образуют группу I₁(n).
Два параллельных зеркала могут представлять группу бесконечного многоугольника I₁(∞), обозначаемую также Ĩ₁.
Три зеркала в виде треугольника образуют образы, которые наблюдаются в традиционном калейдоскопе и такая конфигурация может быть представлена тремя узлами, соединёнными в треугольник. Периодические примеры будут иметь ветви, помеченные как (3 3 3), (2 4 4) и (2 3 6), хотя последние два могут быт нарисованы как прямые (удалив ветви 2). Они генерируют однородные мозаики^[en].
Три зеркала может создать однородный многогранник^[en], включая треугольники Шварца, получаемые из рациональных чисел.
Три зеркала, где одно зеркало перпендикулярно двум другим, могут создать однородные призмы.

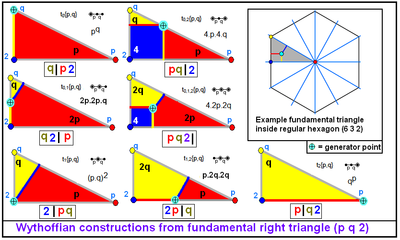Имеется 7 зеркальных однородных конструкций для общего треугольника, основанных на 7 топологических позициях генератора внутри фундаментальной области. Любое единичное активное зеркало имеет генератор в углу и образует ребро, для двух зеркал генератор находится на одной из сторон треугольника, а три активных зеркала имеют генератор внутри треугольника. Одна или две степени свободы можно свести к одной позиции для достижения одинаковых длин рёбер результирующего многогранника или мозаики.	Пример семи генераторов при октаэдральной симметрии^[en] с фундаментальным треугольником (4 3 2) и восьмым генератором обрезка

Двойственные однородные многогранники иногда помечаются вертикальными чертами вместо помеченных кружками узлов, а перечёркнутый пустой узел (без внутренней точки) означает отсечение. Например, представляет прямоугольник (как два активных ортогональных зеркала), а представляет его двойственный многоугольник^[en] (ромб).

Примеры многогранников и мозаик

В качестве примера группа Коксетера B₃ имеет схему . Она также называется октаэдральной симметрией^[en].

Имеется 7 выпуклых однородных многогранников^[en], которые можно построить с помощью этой группы симметрии и 3 из её альтернационных^[en] подсимметрий, каждая с единственной схемой Коксетера — Дынкина. Символ Витгофа^[en] представляет специальный случай схемы Коксетера для графов ранга 3 со всеми тремя ветвями без удаления ветвей порядка 2. Символ Витгофа способен работать с обрезками, но не с общими альтернациями, когда не все узлы помечены кружками.

Однородные октаэдральные многогранники^[en]
Симметрии^[en]^: [4,3], 432^[en]							[4,3]⁺, (432)	[3⁺,4], (3*2)^[en]


{4,3}	t{4,3}	r{4,3}	t{3,4}	{3,4}	rr{4,3}	tr{4,3}	sr{4,3}	s{3,4}
Двойственные многогранники для однородных многогранников

V4³	V3.8²	V(3.4)²	V4.6²	V3⁴	V3.4³	V4.6.8^[en]	V3⁴.4^[en]	V3⁵

Те же построения можно сделать с несвязными (ортогональными) группами Коксетера, наподобие группы однородных призм, и могут рассматриваться с большей ясностью как мозаики диэдров и осоэдров на сфере, наподобие семейств [6]×[] или [6,2]:

Однородные шестиугольные диэдральные сферические многогранники
Симметрия\|: [6,2], (*622)							[6,2]⁺, (622)	[6,2⁺], (2*3)


{6,2}	t{6,2}	r{6,2}	t{2,6}	{2,6}	rr{2,6}	tr{6,2}^[en]	sr{6,2}	s{2,6}
Двойственные им многогранники

V6²	V12²	V6²	V4.4.6^[en]	V2⁶	V4.4.6^[en]	V4.4.12	V3.3.3.6^[en]	V3.3.3.3

По сравнению с [6,3], семейство порождает два параллельных семейства 7 однородных мозаик евклидовой плоскости и их двойственных мозаик. Снова имеется 3 альтернации и несколько полусимметричных версий.

Однородные шестиугольные/треугольные мозаики
Симметрия^[en]^: [6,3], (632)							[6,3]⁺ (632)	[6,3⁺] (3*3)
{6,3}	t{6,3}	r{6,3}	t{3,6}	{3,6}	rr{6,3}	tr{6,3}	sr{6,3}	s{3,6}


6³	3.12²^[en]	(3.6)²^[en]	6.6.6	3⁶	3.4.12.4^[en]	4.6.12^[en]	3.3.3.3.6^[en]	3.3.3.3.3.3
Двойственные им однородные мозаики

V6³	V3.12²^[en]	V(3.6)²^[en]	V6³	V3⁶	V3.4.12.4^[en]	V.4.6.12^[en]	V3⁴.6^[en]	V3⁶

На гиперболической плоскости [7,3] семейство порождает два параллельных множества однородных мозаик евклидовой плоскости и двойственных им мозаик. Имеется только одна альтернация (обрезок^[en]), поскольку все ветви нечётные. Много других гиперболических семейств однородных мозаик можно видеть среди однородных мозаик на гиперболической плоскости.

Однородные семиугольные/треугольные мозаики^[en]
Симметрия: [7,3], (*732)^[en]							[7,3]⁺, (732)


{7,3}^[en]	t{7,3}^[en]	r{7,3}^[en]	2t{7,3}^[en]=t{3,7}	2r{7,3}^[en]={3,7}	rr{7,3}^[en]	tr{7,3}^[en]	sr{7,3}^[en]
Однородные двойственные мозаики


V7³^[en]	V3.14.14	V3.7.3.7	V6.6.7	V3⁷^[en]	V3.4.7.4	V4.6.14^[en]	V3.3.3.3.7

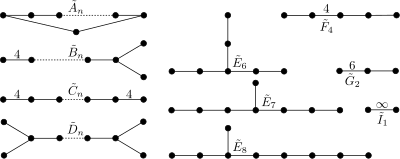
Аффинные группы Коксетера

Семейства выпуклых однородных евклидовых мозаик определяются аффинной группой Коксетера^[en]. Эти группы идеентичны конечным группам с добавлением одного узла. В буквенных обозначениях им даётся та же буква с тильдой («~») над буквой. Индекс относится к конечной группе, так что ранг равен индексу + 1. (Символы Витта^[en] для аффинных групп даны с пометкой также)

${\tilde {A}}_{n-1}$ : диаграммы этого типа являются циклами. (Также P_n)
${\tilde {C}}_{n-1}$ ассоциирована с семейством гиперкубических правильных мозаик (3, …., 4). (Также R_n)
${\tilde {B}}_{n-1}$ связана с C удалением одного минора. (Таже S_n)
${\tilde {D}}_{n-1}$ связана с C удалением двух миноров. (Также Q_n)
${\tilde {E}}_{6}$ , ${\tilde {E}}_{7}$ , ${\tilde {E}}_{8}$ . (Также T₇, T₈, T₉)
${\tilde {F}}_{4}$ образует {3,4,3,3} правильную мозаику. (Также U₅)
${\tilde {G}}_{2}$ образует 30-60-90 треугольные фундаментальные области. (Также V₃)
${\tilde {I}}_{1}$ состоит из двух параллельных зеркал. (= ${\tilde {A}}_{1}$ = ${\tilde {C}}_{1}$ ) (Also W₂)

Составные группы можно определить как ортогональные системы. Наиболее часто используется ${\tilde {A}}_{1}$ . Так, например, ${\tilde {A}}_{1}^{2}$ представляет квадратные или прямоугольные области на евклидовой плоскости, а ${\tilde {A}}_{1}{\tilde {G}}_{2}$ представляет фундаментальную область в виде треугольной призмы в евклидовом трёхмерном пространстве.

Аффинные группы Коксетера (от 2 до 10 узлов)
Ранг	${\tilde {A}}_{1+}$ (P₂₊)	${\tilde {B}}_{3+}$ (S₄₊)	${\tilde {C}}_{1+}$ (R₂₊)	${\tilde {D}}_{4+}$ (Q₅₊)	${\tilde {E}}_{n}$ (T_n+1) / ${\tilde {F}}_{4}$ (U₅) / ${\tilde {G}}_{2}$ (V₃)
2	${\tilde {A}}_{1}$ =[∞]		${\tilde {C}}_{1}$ =[∞]
3	${\tilde {A}}_{2}$ =[3^[3]] *		${\tilde {C}}_{2}$ =[4,4] *		${\tilde {G}}_{2}$ =[6,3] *
4	${\tilde {A}}_{3}$ =[3^[4]] *	${\tilde {B}}_{3}$ =[4,3^1,1] *	${\tilde {C}}_{3}$ =[4,3,4] *	${\tilde {D}}_{3}$ =[3^1,1,3⁻¹,3^1,1] = ${\tilde {A}}_{3}$
5	${\tilde {A}}_{4}$ =[3^[5]] *	${\tilde {B}}_{4}$ =[4,3,3^1,1] *	${\tilde {C}}_{4}$ =[4,3²,4] *	${\tilde {D}}_{4}$ =[3^1,1,1,1] *	${\tilde {F}}_{4}$ =[3,4,3,3] *
6	${\tilde {A}}_{5}$ =[3^[6]] *	${\tilde {B}}_{5}$ =[4,3²,3^1,1] *	${\tilde {C}}_{5}$ =[4,3³,4] *	${\tilde {D}}_{5}$ =[3^1,1,3,3^1,1] *
7	${\tilde {A}}_{6}$ =[3^[7]] *	${\tilde {B}}_{6}$ =[4,3³,3^1,1]	${\tilde {C}}_{6}$ =[4,3⁴,4]	${\tilde {D}}_{6}$ =[3^1,1,3²,3^1,1]	${\tilde {E}}_{6}$ =[3^2,2,2]
8	${\tilde {A}}_{7}$ =[3^[8]] *	${\tilde {B}}_{7}$ =[4,3⁴,3^1,1] *	${\tilde {C}}_{7}$ =[4,3⁵,4]	${\tilde {D}}_{7}$ =[3^1,1,3³,3^1,1] *	${\tilde {E}}_{7}$ =[3^3,3,1] *
9	${\tilde {A}}_{8}$ =[3^[9]] *	${\tilde {B}}_{8}$ =[4,3⁵,3^1,1]	${\tilde {C}}_{8}$ =[4,3⁶,4]	${\tilde {D}}_{8}$ =[3^1,1,3⁴,3^1,1]	${\tilde {E}}_{8}$ =[3^5,2,1] *
10	${\tilde {A}}_{9}$ =[3^[10]] *	${\tilde {B}}_{9}$ =[4,3⁶,3^1,1]	${\tilde {C}}_{9}$ =[4,3⁷,4]	${\tilde {D}}_{9}$ =[3^1,1,3⁵,3^1,1]
11	…	…	…	…

Гиперболические группы Коксетера

Имеется бесконечно много бесконечных гиперболических групп Коксетера. Гиперболические группы делятся на компактные и некомпактные, где компактные группы имеют ограниченные фундаментальные области. Компактные группы гиперболических симплексов (симплексы Ланнера) существуют для рангов от 3 до 5. Паракомпактные группы симплексов (симплексы Козула) существуют вплоть до ранга 10. Гиперкомпактные (многогранники Винберга) группы исследовались, но полностью ещё не изучены. В 2006 Алкок (Allcock) доказал, что имеется бесконечно много компактных многогранников Винберга для пространств размерности вплоть до 6 и бесконечно много многогранников Винберга для размерностей вплоть до 19^[7], так что полное перечисление невозможно. Все эти фундаментальные области отражений, как симплексов, так и не симплексов, часто называют политопами Коксетера, или, иногда, что менее аккуратно, многогранниками Коксетера.

Гиперболические группы в H²

Модель Пуанкаре фундаментальной области треугольников
Примеры прямоугольных треугольников [p, q]
[3,7]	[3,8]	[3,9]	[3,∞]
[4,5]	[4,6]	[4,7]	[4,8]	[∞,4]
[5,5]	[5,6]	[5,7]	[6,6]	[∞,∞]
Примеры треугольников общего вида [(p, q, r)]
[(3,3,4)]	[(3,3,5)]	[(3,3,6)]	[(3,3,7)]	[(3,3,∞)]
[(3,4,4)]	[(3,6,6)]	[(3,∞,∞)]	[(6,6,6)]	[(∞,∞,∞)]

Двумерные гиперболические группы треугольника существуют как схемы Коксетера ранга 3, определяемые треугольником (p q r):

{\frac {1}{p}}+{\frac {1}{q}}+{\frac {1}{r}}<1.

Существует бесконечно много компактных треугольных гиперболических групп Коксетера, включая линейные и треугольные графы. Линейные графы существуют для прямоугольных треугольников (с r=2).^[8]

Компактные гиперболические группы Коксетера

Линейные

Циклические

∞^[en] [p, q],

:
2(p+q)<pq

…

…

…

∞ [(p, q, r)],

: p+q+r>9

			…

Паракомпактные группы Коксетера ранга 3 существуют как пределы компактных.

Линейные графы	Циклические графы
[p,∞] [∞,∞]	[(p, q,∞)] [(p,∞,∞)] [(∞,∞,∞)]

Арифметическая группа треугольника

Конечным подмножеством гиперболических групп треугольника являются арифметические группы. Полный список таких групп нашёл с помощью компьютера Кисао Такеучи (Kisao Takeuchi) и опубликовал в статье 1977 года «Арифметические группы треугольников»^[9]. Имеется таких групп 85, из них 76 компактных и 9 паракомпактных.

Прямоугольные треугольники (p q 2)	Треугольники общего вида (p q r)
Компактные группы: (76) , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , Паракомпактные прямоугольные треугольники: (4) , , ,	Треугольники общего вида: (39) , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , , Паракомпактные треугольники общего вида: (5) , , , ,
(2 3 7), (2 3 8), (2 3 9), (2 3 10), (2 3 11), (2 3 12), (2 3 14), (2 3 16), (2 3 18), (2 3 24), (2 3 30) (2 4 5), (2 4 6), (2 4 7), (2 4 8), (2 4 10), (2 4 12), (2 4 18), (2 5 5), (2 5 6), (2 5 8), (2 5 10), (2 5 20), (2 5 30) (2 6 6), (2 6 8), (2 6 12) (2 7 7), (2 7 14), (2 8 8), (2 8 16), (2 9 18) (2 10 10) (2 12 12) (2 12 24), (2 15 30), (2 18 18) (2 3 ∞) (2,4 ∞) (2,6 ∞) (2 ∞ ∞)	(3 3 4), (3 3 5), (3 3 6), (3 3 7), (3 3 8), (3 3 9), (3 3 12), (3 3 15) (3 4 4), (3 4 6), (3 4 12), (3 5 5), (3 6 6), (3 6 18), (3 8 8), (3 8 24), (3 10 30), (3 12 12) (4 4 4), (4 4 5), (4 4 6), (4 4 9), (4 5 5), (4 6 6), (4 8 8), (4 16 16) (5 5 5), (5 5 10), (5 5 15), (5 10 10) (6 6 6), (6 12 12), (6 24 24) (7 7 7) (8 8 8) (9 9 9) (9 18 18) (12 12 12) (15 15 15) (3,3 ∞) (3 ∞ ∞) (4,4 ∞) (6 6 ∞) (∞ ∞ ∞)

Гиперболические многоугольники Коксетера над треугольниками

Фундаментальная область групп четырёхугольников
Области с идеальными вершинами
or [∞,3,∞] [iπ/λ₁,3,iπ/λ₂] (*3222)	or [((3,∞,3)),∞] [((3,iπ/λ₁,3)), iπ/λ₂] (*3322)	or [(3,∞)^[2]] [(3,iπ/λ₁,3,iπ/λ₂)] (*3232)	or [(4,∞)^[2]] [(4,iπ/λ₁,4,iπ/λ₂)] (*4242)	(*3333)
[iπ/λ₁,∞,iπ/λ₂] (*∞222)	(*∞∞22)	[(iπ/λ₁,∞,iπ/λ₂,∞)] (*2∞2∞)	(*∞∞∞∞)	(*4444)

Другие H² гиперболические калейдоскопы можно построить из многоугольников большего порядка. Подобно группам треугольника эти калейдоскопы можно идентифицировать циклической последовательностью порядков пересечений зеркал вокруг фундаментальной области, как (a b c d …), или, эквивалентно, (согласно нотации орбифолдов^[en]) как *abcd…. Диаграммы Коксетера — Дынкина для этих многоугольных калейдоскопов можно рассматривать как фундаментальную область с вырожденным $(n-1)$ -мерным симплексом с циклическим порядком ветвей a, b, c…, а оставшиеся $n\cdot (n-3)/2$ ветвей помечены как бесконечные (∞) и представляют непересекающиеся зеркала. Единственным негиперболическим примером служит симметрия четырёх зеркал (в евклидовом пространстве) квадрата или прямоугольника, , [∞,2,∞] (орбифолд *2222). Другое представление ветвей непересекающихся зеркал, предложенное Винбергом, показывает бесконечные ветви точечными или пунктирными линиями, так что диаграммы выглядят как с предполагаемыми четырьмя ветвями порядка 2 вокруг периметра.

Например, четырёхугольная область (a b c d) будет иметь две ветви бесконечного порядка, соединяющие ультрапараллельные зеркала. Наименьший гиперболический пример — это , [∞,3,∞] или [iπ/λ₁,3,iπ/λ₂] (орбифолд *3222), где (λ₁,λ₂) является расстоянием между ультрапараллельными зеркалами. Альтернативным выражением является , с тремя ветвями порядка 2, предполагаемыми вокруг периметра. Подобным же образом (2 3 2 3) (орбифолд *3232) можно представить как и (3 3 3 3), (орбифолд *3333) можно представить как полный граф .

Наивысшей квадратной областью (∞ ∞ ∞ ∞) является бесконечный квадрат, представленный полным тетраэдральным графом с 4 ветвями по периметру как идеальные вершины, и двумя диагональными ветвями как бесконечность (показано точечными линиями) для ультрапараллельных^[en] зеркал: .

Компакт (группы симплексов Ланнера)

Компактные гиперболические группы называются группами Ланнера, по имени Фольке Ланнера, изучавшего их в 1950^[10]. Группы существуют только для графов ранга 4 и 5. Коксетер изучал линейные гиперболические группы (своего имени) в статье 1954-го года Regular Honeycombs in hyperbolic space (Регулярные соты в гиперболическом пространстве)^[11], в которой приведены два рациональных решения в 4-мерном гиперболическом пространстве^[en]: [5/2,5,3,3] = и [5,5/2,5,3] = .

Ранги 4-5

Фундаментальная область любой из двух расщепляющихся групп [5,3^1,1] и [5,3,3^1,1] является удвоением соответствующей линейной группы, [5,3,4] и [5,3,3,4] соответственно. Буквенные имена групп даны Джонсоном^[en] как расширение символов Витта^[en]^[12].

Компактные гиперболические группы Коксетера
Размерность H^d	Ранг	Общее число	Линейные	Расщепляющиеся	Циклические
H³	4	9	3:^[en] ${\bar {BH}}_{3}$ = [4,3,5]: ${\bar {K}}_{3}$ = [5,3,5]: ${\bar {J}}_{3}$ = [3,5,3]:	${\bar {DH}}_{3}$ = [5,3^1,1]:	${\widehat {AB}}_{3}$ = [(3³,4)]: ${\widehat {AH}}_{3}$ = [(3³,5)]: ${\widehat {BB}}_{3}$ = [(3,4)^[2]]: ${\widehat {BH}}_{3}$ = [(3,4,3,5)]: ${\widehat {HH}}_{3}$ = [(3,5)^[2]]:
H⁴	5	5	3:^[en] ${\bar {H}}_{4}$ = [3³,5]: ${\bar {BH}}_{4}$ = [4,3,3,5]: ${\bar {K}}_{4}$ = [5,3,3,5]:	${\bar {DH}}_{4}$ = [5,3,3^1,1]:	${\widehat {AF}}_{4}$ = [(3⁴,4)]:

Паракомпакт (группы симплексов Козула)

Паракомпактные (также называемые некомпактными) гиперболические группы Коксетера содержат аффинные подгруппы и имеют симплексные в асимптотике фундаментальные области. Наивысшие паракомпактные гиперболические группы Коксетера имеют ранг 10. Эти группы названы именем французского математика Жана-Луиса Козула^[en]^[13]. Они же называются квазиланнеровскими группами как расширение компактных групп Ланнера. Полный список групп был найден Чейном (M. Chein) с помощью компьютера и опубликован в 1969-м^[14].

Согласно Винбергу, все, кроме восьми, из этих 72 компактных и паракомпактных групп являются арифметическими. Две неарифметические группы компактны — и . Остальные шесть неарифметических групп паракомпактны, из них пять групп являются 3-мерными (, , , и ), а одна является 5-мерной ().

Идеальные симплексы

Имеется 5 гиперболических групп Коксетера, отражающих идеальные симплексы, которые имеют графы, удаление любой одной вершины которых приводит к аффинной группе Коксетера. В этом случае все вершины этих идеальных симплексов находятся на бесконечности^[15].

Ранг	Идеальная группа	Аффинные подгруппы
3	[(∞,∞,∞)]	[∞]
4	[4^[4]]	[4,4]
4	[3^[3,3]]	[3^[3]]
4	[(3,6)^[2]]	[3,6]
6	[(3,3,4)^[2]]	[4,3,3,4], [3,4,3,3]	,

Ранги 4-10

Существует 58 паракомпактных гиперболических групп Коксетера рангами от 4 до 10. Все 58 групп сгруппированы в пять категорий. Буквенные обозначения группам дал Джонсон^[en] как Расширенные символы Витта, для чего он использовал буквы PQRSTWUV из аффинных символов Витта и добавил буквы LMNOXYZ. Над буквами обозначений гиперболических групп присутствует надчёркивание, или крышечка (для циклических схем). Скобочная нотация^[en] Коксетера является линеаризированным представлением группы Коксетера.

Гиперболические паракомпактные группы
Ранг	Полное число	Группы
4	23	${\widehat {BR}}_{3}$ = [(3,3,4,4)]: ${\widehat {CR}}_{3}$ = [(3,4³)]: ${\widehat {RR}}_{3}$ = [4^[4]]: ${\widehat {AV}}_{3}$ = [(3³,6)]: ${\widehat {BV}}_{3}$ = [(3,4,3,6)]: ${\widehat {HV}}_{3}$ = [(3,5,3,6)]: ${\widehat {VV}}_{3}$ = [(3,6)^[2]]:	${\bar {P}}_{3}$ = [3,3^[3]]: ${\bar {BP}}_{3}$ = [4,3^[3]]: ${\bar {HP}}_{3}$ = [5,3^[3]]: ${\bar {VP}}_{3}$ = [6,3^[3]]: ${\bar {DV}}_{3}$ = [6,3^1,1]: ${\bar {O}}_{3}$ = [3,4^1,1]: ${\bar {M}}_{3}$ = [4^1,1,1]:	${\bar {R}}_{3}$ = [3,4,4]: ${\bar {N}}_{3}$ = [4³]: ${\bar {V}}_{3}$ = [3,3,6]: ${\bar {BV}}_{3}$ = [4,3,6]: ${\bar {HV}}_{3}$ = [5,3,6]: ${\bar {Y}}_{3}$ = [3,6,3]: ${\bar {Z}}_{3}$ = [6,3,6]:	${\bar {DP}}_{3}$ = [3^[]x[]]: ${\bar {PP}}_{3}$ = [3^[3,3]]:
5	9	${\bar {P}}_{4}$ = [3,3^[4]]: ${\bar {BP}}_{4}$ = [4,3^[4]]: ${\widehat {FR}}_{4}$ = [(3²,4,3,4)]: ${\bar {DP}}_{4}$ = [3^[3]x[]]:	${\bar {N}}_{4}$ = [4,3,((4,2,3))]: ${\bar {O}}_{4}$ = [3,4,3^1,1]: ${\bar {S}}_{4}$ = [4,3^2,1]:	${\bar {R}}_{4}$ = [(3,4)²]:	${\bar {M}}_{4}$ = [4,3^1,1,1]:
6	12	${\bar {P}}_{5}$ = [3,3^[5]]: ${\widehat {AU}}_{5}$ = [(3⁵,4)]: ${\widehat {AR}}_{5}$ = [(3,3,4)^[2]]:	${\bar {S}}_{5}$ = [4,3,3^2,1]: ${\bar {O}}_{5}$ = [3,4,3^1,1]: ${\bar {N}}_{5}$ = [3,(3,4)^1,1]:	${\bar {U}}_{5}$ = [3³,4,3]: ${\bar {X}}_{5}$ = [3,3,4,3,3]: ${\bar {R}}_{5}$ = [3,4,3,3,4]:	${\bar {Q}}_{5}$ = [3^2,1,1,1]: ${\bar {M}}_{5}$ = [4,3,3^1,1,1]: ${\bar {L}}_{5}$ = [3^1,1,1,1,1]:
7	3	${\bar {P}}_{6}$ = [3,3^[6]]:	${\bar {Q}}_{6}$ = [3^1,1,3,3^2,1]:	${\bar {S}}_{6}$ = [4,3²,3^2,1]:
8	4	${\bar {P}}_{7}$ = [3,3^[7]]:	${\bar {Q}}_{7}$ = [3^1,1,3²,3^2,1]:	${\bar {S}}_{7}$ = [4,3³,3^2,1]:	${\bar {T}}_{7}$ = [3^3,2,2]:
9	4	${\bar {P}}_{8}$ = [3,3^[8]]:	${\bar {Q}}_{8}$ = [3^1,1,3³,3^2,1]:	${\bar {S}}_{8}$ = [4,3⁴,3^2,1]:	${\bar {T}}_{8}$ = [3^4,3,1]:
10	3		${\bar {Q}}_{9}$ = [3^1,1,3⁴,3^2,1]:	${\bar {S}}_{9}$ = [4,3⁵,3^2,1]:	${\bar {T}}_{9}$ = [3^6,2,1]:

Связи подгрупп паракомпактных гиперболических групп

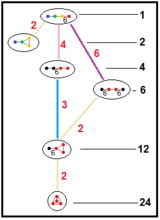
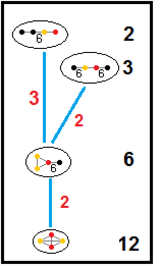
Нижеприведённые графы представляют связи подгрупп паракомпактных гиперболических групп. Индекс подгруппы в каждом ребре дан красным цветом^[16]. Подгруппы с индексом 2 означают удаление зеркала и удвоение фундаментального домена. Другие подгруппы соизмеримы (отношение объёмов является целым числом).

H³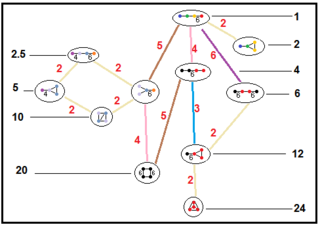
H⁴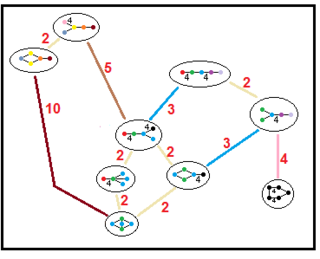
H⁵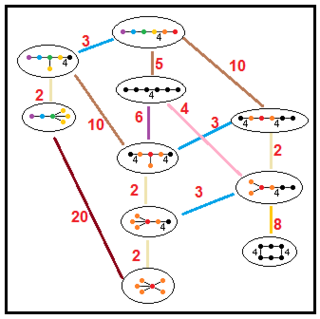

Гиперкомпактные группы Коксетера (политопы Винберга)

Как и для случая гиперболической плоскости H², имеющей нетреугольные многоугольные фундаментальные области, в более высоких размерностях существуют области, не являющиеся симплексами. Эти области можно считать вырожденными симплексами с непересекающимися зеркалами, дающими бесконечный порядок. На схемах Коксетера такие ветви отражаются точечными или пунктирными линиями. Такие области, не являющиеся симплексами, называют политопами Винберга по имени Эрнеста Винберга, разработавшего алгоритм^[en] для поиска несимплексной фундаментальной области гиперболической группы отражений. Геометрически эти фундаментальные области можно классифицировать как четырёхугольные пирамиды или призмы, или другие многогранники со всеми рёбрами, имеющими на них двугранные углы π/n для n=2,3,4…

В симплексных областях имеется n+1 зеркал для n-мерного пространства. В несимплексных областях имеется более чем n+1 зеркал. Список конечен, но полностью ещё не известен. Имеются частичные списки с n+k зеркалами для k, равных 2,3 и 4.

Гиперкомпактные группы Коксетера в трёхмерном пространстве и выше отличаются от двумерных групп в одном существенном отношении. На плоскости два гиперболических n-угольника, имеющие те же самые углы в некотором циклическом порядке, могут иметь различные длины рёбер, и, в общем случае, не конгруэнтны. Политопы Винберга в 3-мерном пространстве и выше полностью определяются двугранными углами. Этот факт базируется на теореме жёсткости Мостова, утверждающей, что две изоморфные группы, образованные отражениями в Hⁿ для n>=3, определяют конгруэнтные фундаментальные области (политопы Винберга).

Политопы Винберга ранга n+2 для n-мерного пространства

Полный список политопов Винберга с рангом зеркал n+2 для n-мерных пространств был дан Эссельманом (F. Esselmann) в 1996^[17]. Частичный список опубликовала в 1974 И. М. Каплинская^[18].

Полный список паракомпактных решений опубликовал П. В. Тумаркин в 2003 для размерностей от 3 до 17^[19].

Наименьший паракомпакт в H³ можно представить как или [∞,3,3,∞], и он может быть построен путём удаления зеркала из паракомпактной гиперболической группы [3,4,4]. Удвоенная фундаментальная область превращается из тетраэдра в четырёхугольную пирамиду. Другие пирамиды включают [4,4,1⁺,4] = [∞,4,4,∞], = . Удаление зеркала из некоторых циклических гиперболических графов Коксетера превращает их в галстуки-бабочки: [(3,3,4,1⁺,4)] = [((3,∞,3)), ((3,∞,3))] или , [(3,4,4,1⁺,4)] = [((4,∞,3)), ((3,∞,4))] или , [(4,4,4,1⁺,4)] = [((4,∞,4)), ((4,∞,4))] или .

Другие паракомпактные графы с фундаментальными областями в виде четырёхугольных пирамид включают:

Размерность	Ранг	Графы
H³	5	, , , , , , , , , , , , , , , , , , , , , , , , , , ,

Ещё одна подгруппа [1⁺,4^1,1,1] = [∞,4,1⁺,4,∞] = [∞^[6]]. = = . ^[20]

Политопы Винберга ранга n+3 для n-мерного пространства

Имеется конечное число вырожденных фундаментальных областей в пространствах до 8 размерности. Полный список компактных политопов Винберга с рангом зеркал n+3 для n-мерных пространств дал П. В. Тумаркин в 2004. Эти группы помечены точечными/пунктирными линиями для ультрапараллельных ветвей.

Для размерностей от 4 до 8, число групп Коксетера ранга от 7 до 11 равно 44, 16, 3, 1 и 1 соответственно^[21]. Группа с наибольшим рангом была открыта Бугаенко в 1984 в пространстве размерности 8, и она имеет ранг 11^[22]:

Dimensions	Rank	Cases	Graphs
H⁴	7	44	…
H⁵	8	16	..
H⁶	9	3
H⁷	10	1
H⁸	11	1

Политопы Винберга ранга n+4 для n-мерного пространства

Существует по конечному числу вырожденных фундаментальных симплексов в размерностях вплоть до восьмой. Компактные политопы Винберга с рангом зеркал n+4 для размерности n исследовали Анна Феликсон и Павел Тумаркин в 2005.^[23]

Группы Лоренца

Правильные соты с группами Лоренца
{3,3,7}^[en] в гиперболическом 3-мерном пространстве. Представлено пересечение сот с плоскостью на бесконечности в модели полупространства Пуанкаре^[en].	{7,3,3}^[en], представленные вне модели шара Пуанкаре.

Группы Лоренца являются группами преобразований Лоренца пространства Минковского. Они имеют связь с геометрией Лоренца, названной именем Хендрика Лоренца, применяемой в специальной теории относительности, и с понятием пространства-времени в общей теории относительности, содержащем времениподобные вектора, скалярное произведение которых на себя даёт отрицательный результат^[12].

В статье 1982-го года Максвелла Упаковка сфер и гиперболические группы отражений (George Maxwell, Sphere Packings and Hyperbolic Reflection Groups) дан список групп Лоренца рангов от 5 до 11. Приведённый им список полон, но не отражает случаи, когда одна группа является подгруппой другой. Имеется бесконечно много групп Лоренца с рангом 4. Для рангов 5-11 имеется конечное число групп Лоренца — 186, 66, 36, 13, 10, 8 и 4 соответственно^[6] В статье 2013-го года Чен и Лаббе (H. Chen, J.-P. Labbé, Lorentzian Coxeter groups and Boyd--Maxwell ball packings) заново пересчитали и дополнили список^[24].

Лоренцевы группы Коксетера
Ранг	Общее число	Группы
4	∞	[3,3,7] … [∞,∞,∞]: … [4,3^[3]] … [∞,∞^[3]]: … [5,4^1,1] … [∞^1,1,1]: … … [(5,4,3,3)] … [∞^[4]]: … … … [4^[]×[]] … [∞^[]×[]]: … … [4^[3,3]] … [∞^[3,3]]
5	186	…[3^[3,3,3]]: …
6	66
7	36	[3^1,1,1,1,1,1]: …
8	13	[3,3,3^[6]]: [3,3^[6],3]: [3,3^[2+4],3]: [3,3^[1+5],3]: [3^{[ ]e×[3]}]:	[4,3,3,3^3,1]: [3^1,1,3,3^3,1]: [3,(3,3,4)^1,1]: [3^2,1,3,3^2,1]:		[4,3,3,3^2,2]: [3^1,1,3,3^2,2]:
9	10	[3,3^[3+4],3]: [3,3^[9]]: [3,3^[2+5],3]:	[3^2,1,3²,3^2,1]:	[3^3,1,3³,4]: [3^3,1,3,3,3^1,1]:	[3^3,3,2]: [3^2,2,4]: [3^2,2,3³,4]: [3^2,2,3,3,3^1,1]:
10	8	[3,3^[8],3]: [3,3^[3+5],3]: [3,3^[9]]:	[3^2,1,3³,3^2,1]:	[3^5,3,1]: [3^3,1,3⁴,4]: [3^3,1,3³,3^1,1]:	[3^4,4,1]:
11	4		[3^2,1,3⁴,3^2,1]:	[3^2,1,3⁶,4]: [3^2,1,3⁵,3^1,1]:	[3^7,2,1]:

Сильно расширенные диаграммы Коксетера

Иногда используется понятие сильно расширенные диаграммы Дынкина, в котором аффинные группы считаются расширенными, гиперболические группы существенно расширенными, а третья ветвь — сильно расширенными простыми группами. Эти расширения обычно помечаются символами 1,2 или 3 + в верхнем индексе для числа расширенных вершин. Эти расширенные серии могут быть расширены в обратном направлении путём последовательного удаления узлов в той же самой позиции графа, хотя процесс останавливается после удаления разветвляющего узла. Расширенное семейство E₈^[en] является наиболее известным примером расширения в обратном направлении из E₃ и вперёд к E₁₁.

Процесс расширения может дать ограниченные серии графов Коксетера, которые проходят путь от конечных к аффинным, затем к гиперболическим и группам Лоренца. Определитель матриц Картана задаёт, где серия меняется от конечной (положительный определитель) к аффинной (нулевой), затем в гиперболический тип (отрицательный), и завершается группой Лоренца, содержащей по меньшей мере одну гиперболическую подгруппу^[25]. Некристаллографические группы H_n образуют расширенную серию, где H₄ расширяется в компактную гиперболическую группу, и существенно расширяется в группу Лоренца.

Определитель матрицы Шлефли по рангам^[26]:

det(A₁ⁿ=[2^n-1]) = 2ⁿ (Конечна для всех n)
det(A_n=[3^n-1]) = n+1 (Конечна для всех n)
det(B_n=[4,3^n-2]) = 2 (Конечна для всех n)
det(D_n=[3^n-3,1,1]) = 4 (Конечна для всех n)

Определитель матрицы Шлефли в исключительных сериях:

det(E_n^[en]=[3^n-3,2,1]) = 9-n (Конечна для E₃(=A₂A₁), E₄(=A₄), E₅(=D₅), E₆, E₇^[en] и E₈, аффинна для E₉ ( ${\tilde {E}}_{8}$ ), гиперболична для E₁₀)
det([3^n-4,3,1]) = 2(8-n) (Конечна для n= от 4 до 7, аффинна для ( ${\tilde {E}}_{7}$ ) и гиперболична для n=8.)
det([3^n-4,2,2]) = 3(7-n) (Конечна для n= от 4 до 6, аффинна для ( ${\tilde {E}}_{6}$ ) и гиперболична для n=7.)
det(F_n=[3,4,3^n-3]) = 5-n (Конечна для F₃(=B₃) и F₄, аффинна для F₅ ( ${\tilde {F}}_{4}$ ), гиперболична для F₆)
det(G_n=[6,3^n-2]) = 3-n (Конечна для G₂, аффинна для G₃ ( ${\tilde {G}}_{2}$ ), гиперболична для G₄)

Мало расширенные серии
	$A_{2}$	$C_{2}$	$G_{2}$	$A_{3}$	$B_{3}$	$C_{3}$	$H_{4}$
Ранг n	[3^[3],3^n-3]	[4,4,3^n-3]	G_n=[6,3^n-2]	[3^[4],3^n-4]	[4,3^1,n-3]	[4,3,4,3^n-4]	H_n=[5,3^n-2]
2	[3] A₂	[4] C₂	[6] G₂		[2] A₁²	[4] C₂	[5] H₂
3	[3^[3]] A₂⁺= ${\tilde {A}}_{2}$	[4,4] C₂⁺= ${\tilde {C}}_{2}$	[6,3] G₂⁺= ${\tilde {G}}_{2}$	[3,3]=A₃	[4,3] B₃	[4,3] C₃	[5,3] H₃
4	[3^[3],3] A₂⁺⁺= ${\bar {P}}_{3}$	[4,4,3] C₂⁺⁺= ${\bar {R}}_{3}$	[6,3,3] G₂⁺⁺= ${\bar {V}}_{3}$	[3^[4]] A₃⁺= ${\tilde {A}}_{3}$	[4,3^1,1] B₃⁺= ${\tilde {B}}_{3}$	[4,3,4] C₃⁺= ${\tilde {C}}_{3}$	[5,3,3] H₄
5	[3^[3],3,3] A₂⁺⁺⁺	[4,4,3,3] C₂⁺⁺⁺	[6,3,3,3] G₂⁺⁺⁺	[3^[4],3] A₃⁺⁺= ${\bar {P}}_{4}$	[4,3^2,1] B₃⁺⁺= ${\bar {S}}_{4}$	[4,3,4,3] C₃⁺⁺= ${\bar {R}}_{4}$	[5,3³] H₅= ${\bar {H}}_{4}$
6				[3^[4],3,3] A₃⁺⁺⁺	[4,3^3,1] B₃⁺⁺⁺	[4,3,4,3,3] C₃⁺⁺⁺	[5,3⁴] H₆
Det(M_n)	3(3-n)	2(3-n)	3-n	4(4-n)	2(4-n)

Средне расширенные серии
	$A_{4}$	$B_{4}$	$C_{4}$	$D_{4}$	$F_{4}$	$A_{5}$	$B_{5}$	$D_{5}$
Ранг n	[3^[5],3^n-5]	[4,3,3^n-4,1]	[4,3,3,4,3^n-5]	[3^n-4,1,1,1]	[3,4,3^n-3]	[3^[6],3^n-6]	[4,3,3,3^n-5,1]	[3^1,1,3,3^n-5,1]
3		[4,3^−1,1] B₂A₁	[4,3] B₃	[3^−1,1,1,1] A₁³	[3,4] B₃		[4,3,3] C₃
4	[3³] A₄	[4,3,3] B₄	[4,3,3] C₄	[3^0,1,1,1] D₄	[3,4,3] F₄		[4,3,3,3^−1,1] B₃A₁	[3^1,1,3,3^−1,1] A₃A₁
5	[3^[5]] A₄⁺= ${\tilde {A}}_{4}$	[4,3,3^1,1] B₄⁺= ${\tilde {B}}_{4}$	[4,3,3,4] C₄⁺= ${\tilde {C}}_{4}$	[3^1,1,1,1] D₄⁺= ${\tilde {D}}_{4}$	[3,4,3,3] F₄⁺= ${\tilde {F}}_{4}$	[3⁴] A₅	[4,3,3,3,3] B₅	[3^1,1,3,3] D₅
6	[3^[5],3] A₄⁺⁺= ${\bar {P}}_{5}$	[4,3,3^2,1] B₄⁺⁺= ${\bar {S}}_{5}$	[4,3,3,4,3] C₄⁺⁺= ${\bar {R}}_{5}$	[3^2,1,1,1] D₄⁺⁺= ${\bar {Q}}_{5}$	[3,4,3³] F₄⁺⁺= ${\bar {U}}_{5}$	[3^[6]] A₅⁺= ${\tilde {A}}_{5}$	[4,3,3,3^1,1] B₅⁺= ${\tilde {B}}_{5}$	[3^1,1,3,3^1,1] D₅⁺= ${\tilde {D}}_{5}$
7	[3^[5],3,3] A₄⁺⁺⁺	[4,3,3^3,1] B₄⁺⁺⁺	[4,3,3,4,3,3] C₄⁺⁺⁺	[3^3,1,1,1] D₄⁺⁺⁺	[3,4,3⁴] F₄⁺⁺⁺	[3^[6],3] A₅⁺⁺= ${\bar {P}}_{6}$	[4,3,3,3^2,1] B₅⁺⁺= ${\bar {S}}_{6}$	[3^1,1,3,3^2,1] D₅⁺⁺= ${\bar {Q}}_{6}$
8						[3^[6],3,3] A₅⁺⁺⁺	[4,3,3,3^3,1] B₅⁺⁺⁺	[3^1,1,3,3^3,1] D₅⁺⁺⁺
Det(M_n)	5(5-n)	2(5-n)		4(5-n)	5-n	6(6-n)	4(6-n)

Некоторые сильно расширенные серии
	$A_{6}$	$B_{6}$	$D_{6}$	$E_{6}$	$A_{7}$	$B_{7}$	$D_{7}$	$E_{7}$	$E_{8}$ ^[en]
Ранг n	[3^[7],3^n-7]	[4,3³,3^n-6,1]	[3^1,1,3,3,3^n-6,1]	[3^n-5,2,2]	[3^[8],3^n-8]	[4,3⁴,3^n-7,1]	[3^1,1,3,3,3,3^n-7,1]	[3^n-5,3,1]	E_n=[3^n-4,2,1]
3									[3^−1,2,1] E₃=A₂A₁
4				[3^−1,2,2] A₂²				[3^−1,3,1] A₃A₁	[3^0,2,1] E₄=A₄
5		[4,3,3,3,3^−1,1] B₄A₁	[3^1,1,3,3,3^−1,1] D₄A₁	[3^0,2,2] A₅				[3^0,3,1] A₅	[3^1,2,1] E₅=D₅
6	[3⁵] A₆	[4,3⁴] B₆	[3^1,1,3,3,3] D₆	[3^1,2,2] E₆		[4,3,3,3,3,3^−1,1] B₅A₁	[3^1,1,3,3,3,3^−1,1] D₅A₁	[3^1,3,1] D₆	[3^2,2,1] E₆ *
7	[3^[7]] A₆⁺= ${\tilde {A}}_{6}$	[4,3³,3^1,1] B₆⁺= ${\tilde {B}}_{6}$	[3^1,1,3,3,3^1,1] D₆⁺= ${\tilde {D}}_{6}$	[3^2,2,2] E₆⁺= ${\tilde {E}}_{6}$	[3⁶] A₇	[4,3⁵] B₇	[3^1,1,3,3,3,3^0,1] D₇	[3^2,3,1] E₇ *	[3^3,2,1] E₇ *
8	[3^[7],3] A₆⁺⁺= ${\bar {P}}_{7}$	[4,3³,3^2,1] B₆⁺⁺= ${\bar {S}}_{7}$	[3^1,1,3,3,3^2,1] D₆⁺⁺= ${\bar {Q}}_{7}$	[3^3,2,2] E₆⁺⁺= ${\bar {T}}_{7}$	[3^[8]] A₇⁺= ${\tilde {A}}_{7}$ *	[4,3⁴,3^1,1] B₇⁺= ${\tilde {B}}_{7}$ *	[3^1,1,3,3,3,3^1,1] D₇⁺= ${\tilde {D}}_{7}$ *	[3^3,3,1] E₇⁺= ${\tilde {E}}_{7}$ *	[3^4,2,1] E₈ *
9	[3^[7],3,3] A₆⁺⁺⁺	[4,3³,3^3,1] B₆⁺⁺⁺	[3^1,1,3,3,3^3,1] D₆⁺⁺⁺	[3^4,2,2] E₆⁺⁺⁺	[3^[8],3] A₇⁺⁺= ${\bar {P}}_{8}$ *	[4,3⁴,3^2,1] B₇⁺⁺= ${\bar {S}}_{8}$ *	[3^1,1,3,3,3,3^2,1] D₇⁺⁺= ${\bar {Q}}_{8}$ *	[3^4,3,1] E₇⁺⁺= ${\bar {T}}_{8}$ *	[3^5,2,1] E₉=E₈⁺= ${\tilde {E}}_{8}$ *
10					[3^[8],3,3] A₇⁺⁺⁺ *	[4,3⁴,3^3,1] B₇⁺⁺⁺ *	[3^1,1,3,3,3,3^3,1] D₇⁺⁺⁺ *	[3^5,3,1] E₇⁺⁺⁺ *	[3^6,2,1] E₁₀=E₈⁺⁺= ${\bar {T}}_{9}$ *
11									[3^7,2,1] E₁₁=E₈⁺⁺⁺ *
Det(M_n)	7(7-n)	2(7-n)	4(7-n)	3(7-n)	8(8-n)	2(8-n)	4(8-n)	2(8-n)	9-n

Геометрические свёртки

Конечные и бесконечные свёртки^[27]
φ_A : A_Γ --> A_Γ' для конечных типов
Γ	Γ'	Описание свёртки	схемы Коксетера — Дынкина
I₂(h)	Γ(h)	Диэдральная свёртка
B_n	A_2n	(I,s_n)
B_n	D_n+1, A_2n-1	(A₃,+/-ε)
F₄	E₆	(A₃,±ε)
H₄	E₈	(A₄,±ε)
H₃	D₆
H₂	A₄
G₂	A₅	(A₅,±ε)
G₂	D₄	(D₄,±ε)
φ: A_Γ⁺ --> A_Γ'⁺ для всех аффинных типов
${\tilde {A}}_{n-1}$	${\tilde {A}}_{kn-1}$	Locally trivial
${\tilde {B}}_{n}$	${\tilde {D}}_{2n+1}$	(I,s_n)
${\tilde {B}}_{n}$	${\tilde {D}}_{n+1}$ , ${\tilde {D}}_{2n}$	(A₃,±ε)
${\tilde {C}}_{n}$	${\tilde {B}}_{n+1}$ , ${\tilde {C}}_{2n}$	(A₃,±ε)
${\tilde {C}}_{n}$	${\tilde {C}}_{2n+1}$	(I,s_n)
${\tilde {C}}_{n}$	${\tilde {A}}_{2n+1}$	(I,s_n) & (I,s₀)
	${\tilde {A}}_{2n}$	(A₃,ε) & (I,s₀)
	${\tilde {A}}_{2n-1}$	(A₃,ε) & (A₃,ε')
${\tilde {C}}_{n}$	${\tilde {D}}_{n+2}$	(A₃,-ε) & (A₃,-ε')
${\tilde {C}}_{2}$	${\tilde {D}}_{5}$	(I,s₁)
${\tilde {F}}_{4}$	${\tilde {E}}_{6}$ , ${\tilde {E}}_{7}$	(A₃,±ε)
${\tilde {G}}_{2}$	${\tilde {D}}_{6}$ , ${\tilde {E}}_{7}$	(A₅,±ε)
	${\tilde {B}}_{3}$ , ${\tilde {F}}_{4}$	(B₃,±ε)
	${\tilde {D}}_{4}$ , ${\tilde {E}}_{6}$	(D₄,±ε)

Схема Коксетера — Дынкина (с простыми связями^[28], конечная, аффинная или гиперболическая), имеющая симметрию (удовлетворяющая одному условию), может быть преобразована с помощью симметрии в новую, в общем случае многониточную схему, с помощью процесса, называемого «свёрткой»^[29]^[30].

Геометрически это соответствует ортогональным проекциям однородных многогранников^[en] и мозаик. Интересно, что любая конечная схема Коксетера — Дынкина с простыми связями может быть свёрнута в I₂(h), где h — Число Коксетера, геометрически соответствующее проекции на плоскость Коксетера^[en].

Некоторые гиперболические свёртки

Примечания

↑ В.О. Бугаенко. Правильные многогранники. — (Математическое просвещение Сер.3).
↑ Brian C. Hall. Lie Groups, Lie Algebras, and Representations: An Elementary Introduction. — Springer, 2003. — ISBN 0-387-40122-9.
↑ Coxeter,. 7.7. Schläfli's Criterion // Regular Polytopes^[en]. — 3rd. — Dover edition, 1973. — С. 133. — ISBN 0-486-61480-8.
↑ В. О. Бугаенко. Классификация многогранников Коксетера // Матем. просв.. — 2003. — Вып. 7. — С. 82—106.
↑ F.Lannér. On complexes with transitive groups of automorphisms. — 1950. — Т. 11. — С. 1–71. — (Medd. Lunds Univ. Mat. Sem. [Comm. Sem. Math. Univ. Lund]).
1 2 George Maxwell, Sphere Packings and Hyperbolic Reflection Groups, JOURNAL OF ALGEBRA 79,78-97 (1982)
↑ Daniel Allcock. Infinitely many hyperbolic Coxeter groups through dimension 19. — Vol. 10. — P. 737–758. — DOI:10.2140/gt.2006.10.737.
↑ The Geometry and Topology of Coxeter Groups, Michael W. Davis, 2008 p. 105 Table 6.2. Hyperbolic diagrams
↑ TAKEUCHI : Arithmetic triangle groups (неопр.) (недоступная ссылка). Projecteuclid.org. Проверено 5 июля 2013. Архивировано 10 июня 2015 года.
↑ Folke Lannér. On complexes with transitive groups of automorphisms. — 1950. — Т. 11. — (Comm. Sém., Math. Univ. Lund [Medd. Lunds Univ. Mat. Sem.]).
↑ Regular Honeycombs in hyperbolic space, Coxeter, 1954
1 2 Norman Johnson, Geometries and Transformations, Chapter 13: Hyperbolic Coxeter groups, 13.6 Lorentzian lattices
↑ J. L. Koszul, Lectures on hyperbolic Coxeter groups, University of Notre Dame (1967)
↑ M. Chein, Recherche des graphes des matrices de Coxeter hyperboliques d’ordre ≤10, Rev. Française Informat. Recherche Opérationnelle 3 (1969), no. Ser. R-3, 3-16 (French).
↑ Subalgebras of hyperbolic Kay-Moody algebras, Figure 5.1, p.13
↑ N.W. Johnson, R. Kellerhals^[en], J.G. Ratcliffe,S.T. Tschantz, Commensurability classes of hyperbolic Coxeter groups H³: p130, H⁴: p137, H⁵: p 138.
↑ F. Esselmann, The classification of compact hyperbolic Coxeter d-polytopes with d+2 facets. Comment. Math. Helvetici 71 (1996), 229—242.
↑ И. М. Каплинская. О дискретных группах, порожденных отражениями в гранях симплициальных призм в пространствах Лобачевского // Матем. заметки. — 1974. — Т. 15, вып. 1. — С. 159—164.
↑ П. В. Тумаркин. Гиперболические многогранники Коксетера в H³ с n+2 гипергранями // Матем. заметки. — 2004. — Т. 75, вып. 6. — С. 909–916.
↑ Norman W. Johnson and Asia Ivic Weiss. Quadratic Integers and Coxeter Groups // Canad. J. Math. — 1999. — Т. Vol. 51, вып. 6. — С. 1307–1336.
↑ П. В. Тумаркин. Гиперболические n-мерные многогранники Кокстера с n+3 гипергранями // УМН. — 2003. — Т. 58, вып. 4(352). — С. 161–162.
↑ В. О. Бугаенко. О группах автоморфизмов унимодулярных гиперболических квадратичных форм над кольцом Z // Вест. МГУ. — 1984. — С. 5, 6-12..
↑ Anna Felikson, Pavel Tumarkin, On compact hyperbolic Coxeter d-polytopes with d+4 facets, 2005
↑ Hao Chen, Jean-Philippe Labbé, Lorentzian Coxeter groups and Boyd-Maxwell ball packings, http://arxiv.org/abs/1310.8608
↑ Kac-Moody Algebras in M-theory
↑ Cartan-Gram determinants for the simple Lie groups, Wu, Alfred C. T, The American Institute of Physics, Nov 1982
↑ John Crisp, 'Injective maps between Artin groups^[en], in Down under group theory, Proceedings of the Special Year on Geometric Group Theory, (Australian National University, Canberra, Australia, 1996), Postscript Архивировано 16 октября 2005 года., pp 13-14, and googlebook, Geometric group theory down under, p 131
↑ то есть имеющая метки ветвей только 3
↑ Jean-Bernard Zuber. Generalized Dynkin diagrams and root systems and their folding. — С. 28–30.
↑ Pierre-Philippe Dechant, Celine Boehm, Reidun Twarock. Affine extensions of non-crystallographic Coxeter groups induced by projection. — October 25, 2011.

Литература для дальнейшего чтения

James E. Humphreys, Reflection Groups and Coxeter Groups, Cambridge studies in advanced mathematics, 29 (1990)
Kaleidoscopes: Selected Writings of H.S.M. Coxeter, edited by F. Arthur Sherk, Peter McMullen, Anthony C. Thompson, Asia Ivic Weiss, Wiley-Interscience Publication, 1995, ISBN 978-0-471-01003-6 , Googlebooks
- (Paper 17) Coxeter, The Evolution of Coxeter-Dynkin diagrams, [Nieuw Archief voor Wiskunde 9 (1991) 233—248]
Coxeter. Chapter 3: Wythoff's Construction for Uniform Polytopes // The Beauty of Geometry: Twelve Essays. — Dover Publications, 1999. — ISBN 978-0-486-40919-1.
- H.S.M. Coxeter. Chapter 5: The Kaleidoscope, Section 11.3 Representation by graphs // Regular Polytopes^[en]. — Dover edition, 1973. — ISBN 0-486-61480-8.
Г.С.М. Коксетер, У.О.Дж. Мозер. Порождающие элементы и определяющие соотношения дискретных групп = H.S.M. Coxeter, W. O. J. Moser, Generators and Relations for Discrete Groups. — Москва: Наука, 1980.
Norman Johnson^[en], Geometries and Transformations, Chapters 11,12,13, preprint 2011
Norman Johnson^[en], R. Kellerhals^[en], J. G. Ratcliffe, S. T. Tschantz. Transformation Groups. — 1999. — Т. 4, вып. 4. — С. 329–353.
Norman W. Johnson, Asia Ivic Weiss. Quadratic Integers and Coxeter Groups // Canad. J. Math. — 1999. — Т. 51, вып. 6. — С. 1307–1336.

Ссылки

Weisstein, Eric W. Coxeter–Dynkin diagram (англ.) на сайте Wolfram MathWorld.
October 1978 discussion on the history of the Coxeter diagrams by Coxeter and Dynkin in Toronto, Canada; Eugene Dynkin Collection of Mathematics Interviews, Библиотека Корнеллского университета^[en].

Данная страница на сайте WikiSort.ru содержит текст со страницы сайта "Википедия".

Если Вы хотите её отредактировать, то можете сделать это на странице редактирования в Википедии.

Если сделанные Вами правки не будут кем-нибудь удалены, то через несколько дней они появятся на сайте WikiSort.ru .

Текст в блоке "Читать" взят с сайта "Википедия" и доступен по лицензии Creative Commons Attribution-ShareAlike; в отдельных случаях могут действовать дополнительные условия.

Другой контент может иметь иную лицензию. Перед использованием материалов сайта WikiSort.ru внимательно изучите правила лицензирования конкретных элементов наполнения сайта.

2019-2025
WikiSort.ru - проект по пересортировке и дополнению контента Википедии

[1] В.О. Бугаенко. Правильные многогранники. — (Математическое просвещение Сер.3).

[2] Brian C. Hall. Lie Groups, Lie Algebras, and Representations: An Elementary Introduction. — Springer, 2003. — ISBN 0-387-40122-9.

[3] Coxeter,. 7.7. Schläfli's Criterion // Regular Polytopes^[en]. — 3rd. — Dover edition, 1973. — С. 133. — ISBN 0-486-61480-8.

[4] В. О. Бугаенко. Классификация многогранников Коксетера // Матем. просв.. — 2003. — Вып. 7. — С. 82—106.

[5] F.Lannér. On complexes with transitive groups of automorphisms. — 1950. — Т. 11. — С. 1–71. — (Medd. Lunds Univ. Mat. Sem. [Comm. Sem. Math. Univ. Lund]).

[Maxwell-6] 1 2 George Maxwell, Sphere Packings and Hyperbolic Reflection Groups, JOURNAL OF ALGEBRA 79,78-97 (1982)

[7] Daniel Allcock. Infinitely many hyperbolic Coxeter groups through dimension 19. — Vol. 10. — P. 737–758. — DOI:10.2140/gt.2006.10.737.

[8] The Geometry and Topology of Coxeter Groups, Michael W. Davis, 2008 p. 105 Table 6.2. Hyperbolic diagrams

[9] TAKEUCHI : Arithmetic triangle groups (неопр.) (недоступная ссылка). Projecteuclid.org. Проверено 5 июля 2013. Архивировано 10 июня 2015 года.

[10] Folke Lannér. On complexes with transitive groups of automorphisms. — 1950. — Т. 11. — (Comm. Sém., Math. Univ. Lund [Medd. Lunds Univ. Mat. Sem.]).

[11] Regular Honeycombs in hyperbolic space, Coxeter, 1954

[johnson2011-12] 1 2 Norman Johnson, Geometries and Transformations, Chapter 13: Hyperbolic Coxeter groups, 13.6 Lorentzian lattices

[13] J. L. Koszul, Lectures on hyperbolic Coxeter groups, University of Notre Dame (1967)

[14] M. Chein, Recherche des graphes des matrices de Coxeter hyperboliques d’ordre ≤10, Rev. Française Informat. Recherche Opérationnelle 3 (1969), no. Ser. R-3, 3-16 (French).

[15] Subalgebras of hyperbolic Kay-Moody algebras, Figure 5.1, p.13

[16] N.W. Johnson, R. Kellerhals^[en], J.G. Ratcliffe,S.T. Tschantz, Commensurability classes of hyperbolic Coxeter groups H³: p130, H⁴: p137, H⁵: p 138.

[17] F. Esselmann, The classification of compact hyperbolic Coxeter d-polytopes with d+2 facets. Comment. Math. Helvetici 71 (1996), 229—242.

[18] И. М. Каплинская. О дискретных группах, порожденных отражениями в гранях симплициальных призм в пространствах Лобачевского // Матем. заметки. — 1974. — Т. 15, вып. 1. — С. 159—164.

[19] П. В. Тумаркин. Гиперболические многогранники Коксетера в H³ с n+2 гипергранями // Матем. заметки. — 2004. — Т. 75, вып. 6. — С. 909–916.

[20] Norman W. Johnson and Asia Ivic Weiss. Quadratic Integers and Coxeter Groups // Canad. J. Math. — 1999. — Т. Vol. 51, вып. 6. — С. 1307–1336.

[21] П. В. Тумаркин. Гиперболические n-мерные многогранники Кокстера с n+3 гипергранями // УМН. — 2003. — Т. 58, вып. 4(352). — С. 161–162.

[22] В. О. Бугаенко. О группах автоморфизмов унимодулярных гиперболических квадратичных форм над кольцом Z // Вест. МГУ. — 1984. — С. 5, 6-12..

[23] Anna Felikson, Pavel Tumarkin, On compact hyperbolic Coxeter d-polytopes with d+4 facets, 2005

[24] Hao Chen, Jean-Philippe Labbé, Lorentzian Coxeter groups and Boyd-Maxwell ball packings, http://arxiv.org/abs/1310.8608

[25] Kac-Moody Algebras in M-theory

[26] Cartan-Gram determinants for the simple Lie groups, Wu, Alfred C. T, The American Institute of Physics, Nov 1982

[27] John Crisp, 'Injective maps between Artin groups^[en], in Down under group theory, Proceedings of the Special Year on Geometric Group Theory, (Australian National University, Canberra, Australia, 1996), Postscript Архивировано 16 октября 2005 года., pp 13-14, and googlebook, Geometric group theory down under, p 131

[28] то есть имеющая метки ветвей только 3

[29] Jean-Bernard Zuber. Generalized Dynkin diagrams and root systems and their folding. — С. 28–30.

[30] Pierre-Philippe Dechant, Celine Boehm, Reidun Twarock. Affine extensions of non-crystallographic Coxeter groups induced by projection. — October 25, 2011.