WikiSort.ru - Не сортированное

Ромбоэдр
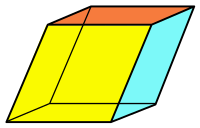Ромбоэдр
Тип	Призма
Свойства	выпуклый многогранник зоноэдр
Комбинаторика
Элементы	12 рёбер 8 вершин
Грани	6 ромбов
Классификация
Группа симметрии	Ci, [2+,2+], (×), порядок 2

Ромбоэдр (от ромб и др.-греч. ἕδρα — основание, грань) — это трёхмерная фигура, наподобие куба, только грани не квадратны, а являются ромбами. Ромбоэдр является частным случаем параллелепипеда, в котором все рёбра равны. Ромбоэдр можно использовать для определения ромбоэдрической решётчатой системы, сот с ромбоэдрическими ячейками.

В общем случае ромбоэдр может иметь три типа ромбических граней, которые разбиваются на конгруэнтные пары противоположных сторон. Ромбоэдр имеет симметрию C_i порядка 2.

Четыре точки, соответствующие несмежным вершинам ромбоэдра, обязательно образуют четыре вершины ортоцентрического тетраэдра и все ортоцентрические тетраэдры могут быть получены таким образом^[1].

Ромбоэдрическая решётчатая система

Ромбоэдрическая решётчатая система имеет ромбоэдрические ячейки с 3 парами уникальных ромбических граней:

В кристаллографии ромбоэдр выделен как простая форма тригональной сингонии средней категории. Минералы, имеющие форму ромбоэдра, — диоптаз, фенакит, многие минералы имеют сложные структуры с наличием ромбоэдра, например, кальцит^{[источник не указан 682 дня]}.

Частные случаи

Вид	Куб	Тригональный трапецоэдр[en]	Прямая ромбическая призма	Ромбическая призма общего вида	Ромбоэдр общего вида
Симметрия	Oh[en], [4,3], порядка 48	D3d, [2+,6], порядка 12	D2h, [2,2], порядка 8	C2h[en], [2], порядка 4	Ci, [2+,2+], порядка 2
Рисунок
Грани	6 квадратов	6 одинаковых ромбов	Два ромба и 4 квадрата	6 ромбические грани	6 ромбические грани

• Куб: с симметрией O_h^[en] порядка 48. Все грани — квадраты.
• Тригональный трапецоэдр^[en]: с симметрией D_3d порядка12. Если все острые внутренние углы граней равны (все грани одинаковы). Тело можно рассматривать как вытягивание куба вдоль главной диагонали. Например, правильный октаэдр с двумя тетраэдрами, приклеенными к противоположным граням, образуют тригональный трапецоэдр с углом 60 градусов. У тригонального трапецоэдра есть хотя бы две вершины, такие, что все прилежащие к ним углы равны между собой. Через эти вершины проходит ось симметрии третьего порядка (то есть такая ось, при повороте вокруг которой на угол 120°=2π/3 тело переходит в само себя). Более того, это является признаком тригонального трапецоэдра: параллелепипед является тригональным трапецоэдром тогда и только тогда, когда он имеет ось симметрии третьего порядка^[2].
• Прямая ромбическая призма: с симметрией D_2h порядка 8. Она строится из двух ромбов и 4 квадратов. Фигуру можно рассматривать как вытягивание куба вдоль диагонали на грани. Например, две треугольные призмы, соединённые по боковой грани, образуют ромбическую призму с углом 60 градусов.
• Ромбическая призма общего вида: с симметрией C_2h^[en] порядка 4. Она имеет только одну плоскость симметрии, проходящую через четыре вершины, и имеет 6 ромбических граней.

Геометрия тела

Для единичного ромбоэдра^[3] (длина стороны = 1), в котором острый ромбический угол равен θ, одна вершина лежит в начале координат (0, 0, 0), а одно ребро лежит на оси x, три вектора равны

e₁: ${\displaystyle {\biggl (}1,0,0{\biggr )},}$

e₂: ${\displaystyle {\biggl (}\cos \theta ,\sin \theta ,0{\biggr )},}$

e₃: ${\displaystyle {\biggl (}\cos \theta ,{(\cos \theta -(\cos \theta )^{2}) \over \sin \theta },{{\sqrt {(1-3(\cos \theta )^{2}+2(\cos \theta )^{3})}} \over sin\theta }{\biggr )}.}$

Другие координаты можно получить из сложения векторов^[4] 3 направлений, e₁ + e₂, e₁ + e₃, e₂ + e₃ и e₁ + e₂ + e_3.

Объём ромбоэдра, длина стороны которого равна a является упрощением формулы объёма параллелепипеда и задаётся формулой

${\displaystyle {\text{Vol}}=a^{3}(1-\cos \theta ){\sqrt {(1+2\cos \theta )}}.}$

Так как площадь основания задаётся формулой ${\displaystyle a^{2}\sin \theta }$ , высота ромбоэдра h задаётся формулой (объём, делённый на площадь основания)

${\displaystyle h={a(1-\cos \theta ){\sqrt {(1+2\cos \theta )}} \over \sin \theta }.}$

Рассмотрим внутренние диагонали ромбоэдра на рисунке. Три из внутренних диагоналей (BG, CF и DE) имеют одну и ту же длину. Их легко вычислить, используя координатную геометрию, если координаты каждой вершины известны. Расстояние в 3-мерном пространстве вычисляется по формуле ^[5]

${\displaystyle d={\sqrt {(x_{2}-x_{1})^{2}+(y_{2}-y_{1})^{2}+(z_{2}-z_{1})^{2}}}.}$

Например, для единичного ромбоэдра с острым углом 72 градуса, три внутренних диагонали (BG, CF и DE) равны 1.543, а длинная диагональ (AH) равна 2.203. Объём этого ромбоэдра равен 0.8789, а высота равна 0.9242.

См. также

• Параллелепипед

Примечания

Литература

Ссылки

• Weisstein, Eric W. Rhombohedron (англ.) на сайте Wolfram MathWorld.
• Volume Calculator https://rechneronline.de/pi/rhombohedron.php

Для улучшения этой статьи желательно: Проверить качество перевода с иностранного языка. Исправить статью согласно стилистическим правилам Википедии.