WikiSort.ru - Не сортированное

Треугольная бипирамида
Тип	Бипирамида и Правильногранный многогранник J11(M3+ A5) - J12(2M1) - J13(2M3)
Коксетер
Шлефли	{ } + {3}
Список граней	6 треугольников
Число рёбер	9
Число вершин	5
Группа симметрии	D3h, [3,2], (*223) порядка 12
Группа вращений	D3, [3,2]+, (223), порядка 6
Тип грани	V3.4.4
Двойственный	Треугольная призма
Свойства	Выпуклый, гранетранзитивный
Развёртка

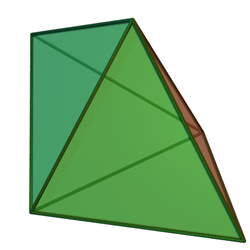
Треугольная бипирамида — это вид шестигранника, первый многогранник в бесконечной последовательности гранетранзитивных бипирамид. Многогранник двойственен треугольной призме.

Как видно из имени, многогранник можно построить путём соединения двух тетраэдров по одной грани. Хотя все грани многогранника конгруэнтны и тело является изоэдральным, оно не является правильным многогранником, поскольку некоторые вершины относятся к трём граням, а другие — к четырём.

Бипирамида, шесть граней которой являются правильными треугольниками, является одним из правильногранных многогранников, (J₁₂ в нотации Джонсона, 2M₁ в нотации Залгаллера). Правильногранный многогранник является одним из 92 строго выпуклых многогранников, имеющих правильные грани, но однородным многогранником^[en] он не является (то есть многогранник не является правильным многогранником, архимедовым телом, призмой или антипризмой). Название многограннику дал Норман Джонсон, который первым перечислил эти многогранники в 1966^[1]. Как правильногранный многогранник, имеющий в качестве граней правильные треугольники, он является также дельтаэдром.

Двойственный многогранник

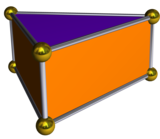
Двойственный многогранник треугольной бипирамиды — треугольная призма с пятью гранями, два параллельных правильных треугольника, связанные цепочкой из трёх прямоугольников. Хотя треугольная призма имеет вид, являющийся однородным многогранником (с квадратными гранями), двойственный многогранник правильногранного вида бипирамиды имеет прямоугольные грани, а не квадратные, так что многогранник не является однородным.

Двойственная треугольная бипирамида	Развёртка двойственного многогранника

Связанные многогранники и соты

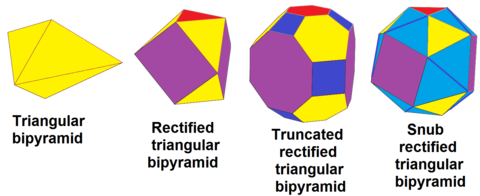
Треугольную бипирамиду dt{2,3} можно видеть в последовательности полноусечённых многогранников, rdt{2,3}, усечённых, trdt{2,3} и альтернированных (плосконосых) многогранников, srdt{2,3}:

Треугольная бипирамида может быть построена путём наращивания более мелких частей, в частности, из двух правильных октаэдров один над другим с 3 треугольными бипирамидами, добавленными вокруг сторон и по 1 тетраэдру сверху и снизу. Этот многогранник имеет 24 грани в виде правильных треугольников, но правильногранным многогранником он не является, поскольку имеет грани, находящиеся в одной плоскости (копланарные грани). Этот многогранник является копланарным дельтаэдром с 24 треугольными гранями. Этот многогранник получается путём наращивания ячеек в скрученных альтернированных кубических сотах^[en]. Бо́льшие треугольные многогранники можно получить аналогичным образом с 9, 16 или 25 треугольниками на большой треугольной грани, что можно рассматривать как часть треугольной мозаики.

Треугольная бипирамида может образовывать замощение пространства с октаэдрами или усечёнными тетраэдрами^[2].

Слои однородных четвертькубических сот[en] можно сдвинуть с образованием пар тетраэдральных ячеек, которые комбинируются в треугольные бипирамиды.

скрученные тетраэдральнооктаэдральные соты[en] имеют пары смежных правильных тетраэдров, которые можно рассматривать как треугольные бипирамиды.

См. также

Семейство бипирамид

Многогранник
Мозаика
Конфигурация	V2.4.4	V3.4.4	V4.4.4	V5.4.4	V6.4.4	V7.4.4	V8.4.4	V9.4.4	V10.4.4	...V∞.4.4

Примечания

Литература

Ссылки

• Weisstein, Eric W. Triangular dipyramid (англ.) на сайте Wolfram MathWorld.
• Conway Notation for Polyhedra Try: dP3

Для улучшения этой статьи желательно: Проверить качество перевода с иностранного языка. Исправить статью согласно стилистическим правилам Википедии.