WikiSort.ru - Не сортированное

Звёздчатый октаэдр
Тип	Правильное соединение многогранников
Граней	8 треугольников
Рёбер	12
Вершин	8
Группы симметрии Группа Коксетера	Октаэдральная (Oh) [4,3] or [[3,3]]
Ядро	Октаэдр
Символ Шлефли	${\displaystyle 3}$
Символ Коксетера	{4,3}[2{3,3}]{3,4}[1]
Диаграмма Коксетера	∪ =
Выпуклая оболочка	Куб
Index	UC4, W19[en]
Двойственный	Самодвойственен

Звёздчатый октаэдр, или stella octangula, — это единственная звёздчатая форма октаэдра. Латинским именем stella octangula многогранник назвал Кеплер в 1609, хотя он был известен более ранним геометрам^[en]. Так, он изображён в труде Пачоли Divina Proportione, 1509.

Многогранник является простейшим из пяти правильных соединений многогранников.

Звёздчатый октаэдр можно рассматривать как трёхмерное обобщение гексаграммы — гексаграмма является двумерной фигурой, образованной двумя наложенными друг на друга правильными треугольниками, центрально симметричными друг другу, и точно таким же образом звёздчатый октаэдр может быть образован из двух центрально симметричных пересекающихся тетраэдров. Его же можно рассматривать как одну из стадий построения 3D-снежинки Коха, фрактальной фигуры, получаемой повторяющимся присоединением меньших тетраэдров к каждой треугольной поверхности большей фигуры. Начальной стадией построения снежинки Коха является один центральный тетраэдр, а второй стадией, полученной добавлением четырёх меньших тетраэдров к граням центрального тетраэдра, и будет звёздчатый октаэдр.

Построение

Звёздчатый октаэдр можно получить несколькими путями:

• Это образование звёздчатой формы правильного октаэдра, сохраняющее его плоскости граней. Грани звезды очень простые: (См. модель Веннинджера W₁₉).
• Он является правильным соединением многогранников, если строить как объединение двух тетраэдров (тетраэдр и двойственный ему тетраэдр).
• Его можно получить дополнением правильного октаэдра треугольными пирамидами к каждой грани. В этом построении многогранник имеет ту же топологию, что и выпуклое каталаново тело триакисоктаэдр, имеющее куда более короткие пирамиды.
• Это огранка куба с сохранением вершин.

Связанные концепции

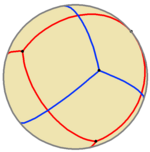
Можно построить соединение двух сферических тетраэдров, как показано на рисунке.

Два тетраэдра в соединении звёздчатого октаэдра являются «десмичными», что означает (если рассматривать их как прямые в проективном пространстве), что каждое ребро одного тетраэдра пересекает противоположное ребро другого тетраэдра. Одно из таких пересечений видно в звёздчатом октаэдре. Другое пересечение оказывается в бесконечной точке проективной плоскости между двумя параллельными рёбрами двух тетраэдров. Эти два тетраэдра могут быть дополнены до десмичной системы^[en] трёх тетраэдров, где третий тетраэдр имеет в качестве чётырёх вершин три точки пересечения на бесконечности и центроид двух конечных тетраэдров. Те же самые двенадцать вершин тетраэдров образуют точки конфигурации Рейе.

Числа звёздчатого октаэдра — это фигурные числа, подсчитывающие число шаров, которые можно расположить внутри звёздчатого октаэдра. Эти числа равны

0, 1, 14, 51, 124, 245, 426, 679, 1016, 1449, 1990, … (последовательность A007588 в OEIS)

В популярной культуре

Звёздчатый октаэдр представлен наряду с некоторыми другими многогранниками и соединениями многогранников на картинах Эшера «Звёзды»^{[en] [2]} и «Двойной астероид» (1949)^[3].

Галерея

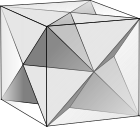
Это полная симметрическая огранка куба

Примечания

Литература

Внешние ссылки

• VRML модель:
• MathWorld, Stella Octangula
• KlitzingPolytopes|../incmats/so.htm Richard Klitzing, 3D compound

Для улучшения этой статьи желательно: Проверить качество перевода с иностранного языка. Исправить статью согласно стилистическим правилам Википедии.