WikiSort.ru - Не сортированное

Однородная квадратная антипризма
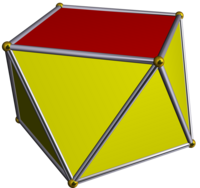Квадратная антипризма
Тип	Призматический однородный многогранник
Свойства	выпуклый многогранник
Комбинаторика
Элементы	16 рёбер 8 вершин
Грани	8 треугольников 2 квадрата
Конфигурация вершины	3.3.3.4
Развёртка
Двойственный многогранник	Тетрагональный трапецоэдр[en]
Классификация
Символ Шлефли	s{2,8} sr{2,4}
Символ Витхоффа[en]	| 2 2 4
Диаграмма Дынкина
Группа симметрии	D4, [4,2]+, (442), порядок=8

Квадратная антипризма — это второй многогранник в бесконечном ряду антипризм, образованных последовательностью треугольных граней, закрытых с обеих сторон многоугольниками. Квадратная антипризма известна также как антикуб^[1].

Если все грани являются правильными многоугольниками, антипризма является полуправильным многогранником или однородным многогранником^[en].

Точки на сфере

Если восемь точек разместить на сфере с целью максимизации расстояний между ними в некотором смысле, получившаяся фигура соответствует скорее квадратной антипризме, чем кубу. Специфичные методы распределения точек включают, например, задачу Томпсона^[en] (минимизация суммы обратных величин расстояний между точками), максимизацию расстояний от точки до ближайшей или минимизацию суммы всех обратных квадратов расстояний между точками.

Молекулы с квадратной антипризматической геометрией

Согласно теории ОЭПВО молекулярной геометрии^[en] в химии, которая основывается на принципе максимизации расстояний между точками, квадратная антипризма является наиболее предпочтительной геометрией, если восемь пар электронов окружают центральный атом. Одна из молекул с такой геометрией — ион октафтороксената (VI) (XeF₈²⁻) в соли октафтороксената(VI) нитрозила^[en]. Однако молекула эта далека от идеальной квадратной антипризмы^[2]. Очень мало ионов имеют кубическую форму, поскольку такая форма привела бы к сильному отталкиванию лигандов. PaF₈³⁻ является одним из немногих примеров^[3].

Кроме того, сера образует восьмиатомные молекулы S₈ как наиболее устойчивую аллотропную форму. Молекула S₈ имеет структуру, основанную на квадратной антипризме. В этой молекуле атомы занимают восемь вершин антипризмы, а восемь рёбер между рёбрами соответствуют ковалентной связи между атомами серы.

В архитектуре

Главное здание в комплексе Центра международной торговли (на месте старого Центра международной торговли, разрушенного 11 сентября 2001) имеет форму очень высокой сужающейся к верху квадратной антипризмы. Здание не является истинной антипризмой, поскольку она сужается к верху — верхний квадрат имеет вдвое меньшую площадь по сравнению с основанием.

Топологически эквивалентные многогранники

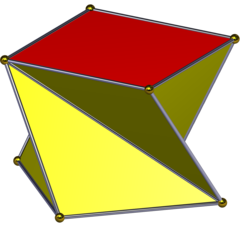
Скрученная призма (по часовой стрелке или против часовой стрелки) может иметь то же расположение вершин. Этот многогранник можно рассматривать как форму, собранную из 4 тетраэдров с вырезанными частями. Однако после вырезания тело нельзя разбить на тетраэдры без добавления новых вершин. Тело имеет половину симметрий однородного тела: D_n, [4,2]^+[4][5].

Связанные многогранники

Производные многогранники

Скрученно удлинённая четырёхугольная пирамида является правильногранным многогранником (J₁₀ = М₂+А₄), полученным удлинением квадратной пирамиды. Подобным же образом, скрученно удлинённая четырёхугольная бипирамида (J₁₇ = М₂+А₄+М₂) является дельтаэдром (многогранником, грани которого являются правильными треугольниками), построенным путём замены обоих квадратов квадратной антипризмы квадратными пирамидами.

Плосконосый двуклиноид(J₈₄ = М₂₅) является другим дельтаэдром, который получается заменой двух квадратов квадратной антипризмы парами равносторонних треугольников. Плосконосую квадратную антипризму (J₈₅ = М₂₈) можно рассматривать как квадратную антипризму, полученную путём вставки цепочки равносторонних треугольников. Клинокорона (J₈₆ = М₂₁) и большая клинокорона (J₈₈ = М₂₃) являются другими правильногранными многогранниками, которые, подобно другим квадратным антипризмам, состоят из двух квадратов и чётного числа равносторонних треугольников.

Квадратная антипризма может быть усечена и альтернирована для образования плосконосых антипризм:

Плосконосые антипризмы

Антипризма	Усечение t	Альтернирование[en] ht
s{2,8}	ts{2,8}	ss{2,8}

Аналогичные многогранники

Будучи антипризмой, квадратная антипризма принадлежит семейству многогранников, в которые входят октаэдр (который можно рассматривать как треугольную антипризму), пятиугольная антипризма, шестиугольная антипризма и восьмиугольная антипризма^[en].

Семейство однородных антипризм n.3.3.3

Многогранник
Мозаика
Конфигурация	V2.3.3.3	3.3.3.3	4.3.3.3	5.3.3.3	6.3.3.3	7.3.3.3	8.3.3.3	9.3.3.3	10.3.3.3	11.3.3.3	12.3.3.3	17.3.3.3	...∞.3.3.3

Квадратная антипризма является первой в ряду плосконосых многогранников и мозаик с вершинной фигурой 3.3.4.3.n.

4n2 симметрии плосконосых мозаик: 3.3.4.3.n
Симметрия 4n2	Сферическая		Евклидова	Компактная гиперболическая				Paracomp.
	242	342	442	542	642	742	842	∞42
Плосконосые мозаики
Конфиг.	3.3.4.3.2	3.3.4.3.3	3.3.4.3.4	3.3.4.3.5	3.3.4.3.6	3.3.4.3.7	3.3.4.3.8	3.3.4.3.∞
Гиро- мозаики
Конфиг.	V3.3.4.3.2	V3.3.4.3.3	V3.3.4.3.4	V3.3.4.3.5	V3.3.4.3.6	V3.3.4.3.7	V3.3.4.3.8	V3.3.4.3.∞

См. также

• Комбинация трёх квадратных антипризм^[en]

Примечания

Литература

Ссылки

• Weisstein, Eric W. Antiprism (англ.) на сайте Wolfram MathWorld.
• Square Antiprism Интерактивная модель
• Virtual Reality Polyhedra www.georgehart.com: The Encyclopedia of Polyhedra
  • VRML model
  • Conway Notation for Polyhedra Try: «A4»

Для улучшения этой статьи желательно: Проверить качество перевода с иностранного языка. Исправить статью согласно стилистическим правилам Википедии.