

Дельтаэдр — это многогранник, все грани которого являются правильными треугольниками. Название взято от греческой заглавной буквы дельта ( ), которая имеет форму равностороннего треугольника. Существует бесконечно много дельтаэдров, но из них только восемь выпуклы, и они имеют 4, 6, 8, 10, 12, 14, 16 и 20 граней[1].
Число граней, рёбер и вершин перечислены ниже для каждого из восьми дельтаэдров.
Выпуклые дельтаэдры
Всего существует 8 выпуклых дельтаэдров[2], 3 из которых являются платоновыми телами, а 5 — многогранниками Джонсона.
У дельтаэдра с 6 гранями некоторые вершины имеют степень 3, а некоторые — степень 4. В дельтаэдрах с 10, 12, 14 и 16 гранями некоторые вершины имеют степень 4, а некоторые — степень 5. Эти пять неправильных дельтаэдров принадлежат классу правильногранных многогранников — выпуклых многогранников с правильными многоугольниками в качестве граней.
Не существует выпуклого дельтаэдра с 18 гранями[3]. Однако икосаэдр со стянутым ребром[en] даёт пример октаэдра, который либо может быть сделан выпуклым с 18 неправильными гранями, либо с двумя наборами по три равносторонних треугольника, лежащими в одной плоскости.
| Правильные дельтаэдры | ||||||
|---|---|---|---|---|---|---|
| Название | Изображение | Количество вершин |
Количество рёбер |
Количество граней |
Конфигурация вершины |
Группа симметрии |
| Правильный тетраэдр |  |
4 | 6 | 4 | 4 × 33 | Td, [3,3] |
| Правильный октаэдр (четырёхугольная бипирамида) |  |
6 | 12 | 8 | 6 × 34 | Oh, [4,3] |
| Правильный икосаэдр |  |
12 | 30 | 20 | 12 × 35 | Ih, [5,3] |
| Дельтаэдры Джонсона | ||||||
| Треугольная бипирамида |  |
5 | 9 | 6 | 2 × 33 3 × 34 |
D3h, [3,2] |
| Пятиугольная бипирамида |  |
7 | 15 | 10 | 5 × 34 2 × 35 |
D5h, [5,2] |
| Плосконосый двуклиноид |  |
8 | 18 | 12 | 4 × 34 4 × 35 |
D2d, [2,2] |
| Трижды наращённая треугольная призма |  |
9 | 21 | 14 | 3 × 34 6 × 35 |
D3h, [3,2] |
| Скрученно удлинённая четырёхугольная бипирамида |  |
10 | 24 | 16 | 2 × 34 8 × 35 |
D4d, [4,2] |
Нестрого выпуклые случаи
Существует бесконечно много дельтаэдров с копланарными (лежащими в одной плоскости) треугольниками. Если множества копланарных треугольников считаются одной гранью, можно насчитать меньше граней, рёбер и вершин. Копланарные треугольные грани могут быть слиты в ромбические, трапециевидные, шестиугольные или другие равносторонние многоугольные грани. Каждая грань должна быть выпуклым полиамондом, таким как ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Некоторые небольшие примеры
| Рисунок | Название | Граней | Рёбер | Вершин | Конфигурации вершин | Группа симметрии |
|---|---|---|---|---|---|---|
 |
Наращенный октаэдр[en] Наращение 1 тетр. + 1 окт. |
10 | 15 | 7 | 1 × 33 3 × 34 3 × 35 0 × 36 |
C3v, [3] |
| 4 3 | 12 | |||||
 |
Треугольный трапецоэдр[en] Наращение 2 тетр. + 1 окт. |
12 | 18 | 8 | 2 × 33 0 × 34 6 × 35 0 × 36 |
C3v, [3] |
| 6 | 12 | |||||
 |
Наращение 2 тетр. + 1 окт. |
12 | 18 | 8 | 2 × 33 1 × 34 4 × 35 1 × 36 |
C2v, [2] |
| 2 2 2 | 11 | 7 | ||||
 |
Треугольная усечённая пирамида Наращение 3 тетр. + 1 окт. |
14 | 21 | 9 | 3 × 33 0 × 34 3 × 35 3 × 36 |
C3v, [3] |
| 1 3 1 | 9 | 6 | ||||
 |
Удлинённый октаэдр[en] Наращение 2 тетр. + 2 окт. |
16 | 24 | 10 | 0 × 33 4 × 34 4 × 35 2 × 36 |
D2h, [2,2] |
| 4 4 | 12 | 6 | ||||
 |
Тетраэдр Наращение 4 тетр. + 1 окт. |
16 | 24 | 10 | 4 × 33 0 × 34 0 × 35 6 × 36 |
Td, [3,3] |
| 4 | 6 | 4 | ||||
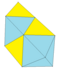 |
Наращение 3 тетр. + 2 окт. |
18 | 27 | 11 | 1 × 33 2 × 34 5 × 35 3 × 36 |
D2h, [2,2] |
| 2 1 2 2 | 14 | 9 | ||||
 |
Икосаэдр со стянутым ребром[en] | 18 | 27 | 11 | 0 × 33 2 × 34 8 × 35 1 × 36 |
C2v, [2] |
| 12 2 | 22 | 10 | ||||
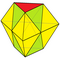 |
Двуусечённая бипирамида[en] Наращение 6 тетр. + 2 окт. |
20 | 30 | 12 | 0 × 33 3 × 34 6 × 35 3 × 36 |
D3h, [3,2] |
| 2 6 | 15 | 9 | ||||
 |
Трёхскатный купол Наращение 4 тетр. + 3 окт. |
22 | 33 | 13 | 0 × 33 3 × 34 6 × 35 4 × 36 |
C3v, [3] |
| 3 3 1 1 | 15 | 9 | ||||
 |
Треугольная бипирамида Наращение 8 тетр. + 2 окт. |
24 | 36 | 14 | 2 × 33 3 × 34 0 × 35 9 × 36 |
D3h, [3] |
| 6 | 9 | 5 | ||||
 |
Шестиугольная антипризма | 24 | 36 | 14 | 0 × 33 0 × 34 12 × 35 2 × 36 |
D6d, [12,2+] |
| 12 2 | 24 | 12 | ||||
 |
Усечённый тетраэдр Наращение 6 тетр. + 4 окт. |
28 | 42 | 16 | 0 × 33 0 × 34 12 × 35 4 × 36 |
Td, [3,3] |
| 4 4 | 18 | 12 | ||||
 |
Тетракискубоктаэдр[en] Октаэдр Наращение 8 тетр. + 6 окт. |
32 | 24 | 18 | 0 × 33 12 × 34 0 × 35 6 × 36 |
Oh, [4,3] |
| 8 | 12 | 6 |
Невыпуклые дельтаэдры
Невыпуклых и тороидальных дельтаэдров существует бесконечно много.
Пример дельтаэдра с самопересекающимися гранями
- Большой икосаэдр — тело Кеплера — Пуансо, с 20 пересекающимися треугольниками
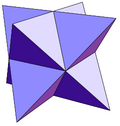
Другие невыпуклые дельтаэдры можно получить путём добавления пирамид к граням всех 5 правильных многогранников:
 |
 |
 |
 |
 |
| Триакистетраэдр | Тетракисгексаэдр | Триакисоктаэдр (stella octangula) |
Пентакисдодекаэдр | Триакисикосаэдр |
|---|---|---|---|---|
| 12 треугольников | 24 треугольников | 60 треугольников | ||
Другие наращения тетраэдров:
 |
 |
 |
| 8 треугольников | 10 треугольников | 12 треугольников |
|---|
Также путём добавления к граням перевёрнутых пирамид:
 Выемчатый додекаэдр[en] |
 Тороидальный дельтаэдр |
| 60 треугольников | 48 треугольников |
|---|
Примечания
Литература
- Freudenthal H., van der Waerden B. L. Over een bewering van Euclides ("On an Assertion of Euclid") // Simon Stevin. — 1947. — Т. 25. — С. 115–128. (Авторы показали, что существует только 8 выпуклых дельтаэдров. )
- Charles W. Trigg. An Infinite Class of Deltahedra // Mathematics Magazine. — 1978. — Т. 51, вып. 1. — С. 55–57.
Для улучшения этой статьи желательно: |
Данная страница на сайте WikiSort.ru содержит текст со страницы сайта "Википедия".
Если Вы хотите её отредактировать, то можете сделать это на странице редактирования в Википедии.
Если сделанные Вами правки не будут кем-нибудь удалены, то через несколько дней они появятся на сайте WikiSort.ru .

