Эта статья предлагается к удалению. |
| Четырнадцатиугольник | |
|---|---|
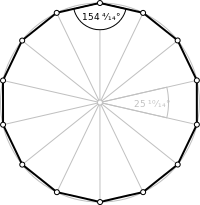 Правильный четырнадцатиугольник | |
| Тип | Правильный многоугольник |
| Рёбра | 14 |
| Символ Шлефли | {14}, t{7} |
| Диаграмма Коксетера — Дынкина |
|
| Вид симметрии | Диэдрическая группа (D18) порядок 2×18 |
| Внутренний угол (градусы) | 154° |
| Свойства | выпуклый, вписанный, равносторонний, равноугольный[en], изотоксальный |
Четырнадцатиугольник или тетрадекагон — это многоугольник с четырнадцатью сторонами.
Симметрия

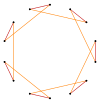
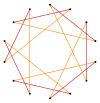
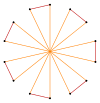
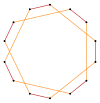
Правильный четырнадцатиугольник имеет симметрию Dih14 порядка 36. Имеется 5 типов подгрупп диэдральной симметрии: Dih9, (Dih6, Dih3) и (Dih2, Dih1), а также 6 циклических групп симметрии: (Z14, Z9), (Z6, Z3) и (Z2, Z1).
Справа на рисунке можно видеть 10 симметрий четырнадцатиугольника. Конвей использовал для обозначения симметрий буквы вместе с порядком группы[1]. Полная симметрия правильной фигуры будет равна r36, а отсутствие симметрии отмечается как a1. Диэдральные симметрии делятся по тому, проходят они через вершины (используется буква d, от «diagonal») или через середины сторон (используется буква p, от «perpendicular»). Если же оси симметрии проходит через вершины и середины сторон, используется буква i. Циклические симметрии помечаются буквой g (от «gyration»). Каждая подгруппа симметрии допускает одну или более степеней свободы для неправильных форм. Только подгруппа g14 не даёт свободы, но стороны многоугольника могут рассматриваться как имеющие направление.
Правильный четырнадцатиугольник
Площадь правильного четырнадцатиугольника со стороной a задаётся формулой
Построение четырнадцатиугольника
Правильный четырнадцатиугольник нельзя построить с помощью циркуля и линейки[2]. Однако, его можно построить с помощью метода невсиса, если использовать его вместе с трисекцией угла,[3] или с линейкой с метками[4] как показано на следующих двух примерах.

Анимация (1м 47с) с помощью метода невсиса построения четырнадцатиугольника в окружности радиуса , опираясь на трисекцию угла с помощью томагавка.
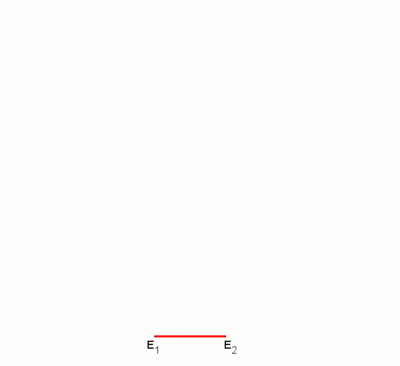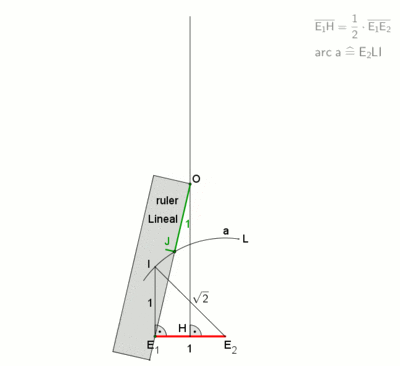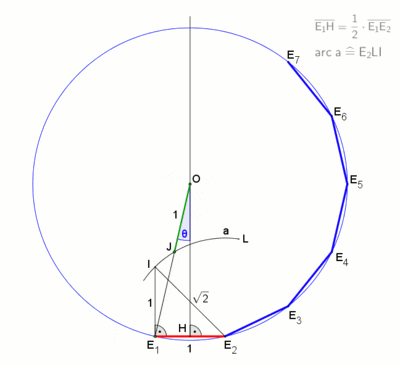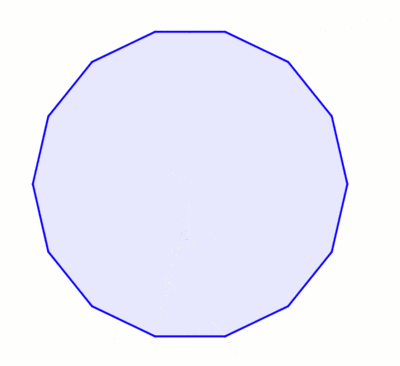
Анимация (1м 20с) построения с помощью метода невсиса с применением маркированой линейки (согласно Дэвиду Джонсону Лейсикц[4]

Четырнадцатиугольник Петри
У правильного четырнадцатиугольника существуют 5 правильных четырнадцатиугольников.
- Гептеракт
- 7-ортоплекс
- 7-7 дуопирамида
- 7-7 дуопризма
- 13-симплекс
Рассечение
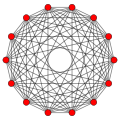
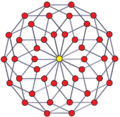
Коксетер утверждает, что любой 2m-угольник с параллельными сторонами можно разбить на m(m-1)/2 ромбов. Для правильного четырнадцатиугольника m=7 и его можно разбить на 21 ромб — на 3 набора по 7 ромбов. Это разбиение основано на проекции многоугольника Петри гептеракта с 21 из 672 граней[5]. Список A006245 даёт число решений 24698, включая вращения и хиральные формы.
 |
 |
В Малайзии




- В виде правильного 14-угольника чеканятся некоторые памятные золотые и серебряные малайзийские монеты. Число сторон в них символизирует число штатов Малайзийской Федерации.
- 14-лучевая звезда изображена на гербе Малайзии, её государственном флаге и флаге и эмблеме её вооружённых сил.
В традиционном искусстве
Шаманский этнический 14-угольный бубен, выполненный в германской традиции.[6].
Четырнадцатиугольник также использовался в исламских декоративных узорах[7].
Другое
Компьютерная игра Tetradecagon.
Абстрактный рисунок Momentia:Tetradecagon (Gaurav Bose, India)
В архитектуре: Glashouse (Bruno Taut, 1914)[8]. Хор в форме четырнадцатиугольника в церкви св. Николая в Бари[9]. Апсида церкви в Понтиньи состоит из семи сторон четырнадцатиугольника и дополнительного полупролета.
Связанные фигуры
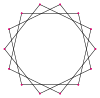
Четырнадцатиугольник имеет 14 сторон и представляется символом {14/n}. Имеется два правильных звёздчатых многоугольника — {14/3} и {14/5}, использующих те же самые вершины, но соединённые через три или через пять точек. Существует также три составных четырнадцатиугольника — {14/2} сводится к 2{7} (два семиугольника), а {14/4} и {14/6} сводятся к 2{7/2} и 2{7/3} (две различные гептаграммы), и, наконец, {14/7} сводится к семи двуугольникам.
Более глубокие усечения правильного семиугольника и гептаграмм может дать изогональные (вершинно-транзитивные) промежуточные формы с равным расстоянием между вершинами и двумя длинами рёбер. Другие усечения могут дать многоугольники двойного накрытия 2{p/q}, а именно: t{7/6}={14/6}=2{7/3}, t{7/4}={14/4}=2{7/2} и t{7/2}={14/2}=2{7}[10].
Примечания
- ↑ Conway, Burgiel, Goodman-Strass, 2008, с. 275—278.
- ↑ Wantzel, 1837, с. 366–372.
- ↑ Gleason, 1988, с. 185–194.
- 1 2 Weisstein, Eric W. «Heptagon.» From MathWorld, A Wolfram Web Resource.
- ↑ Ball, Coxeter, 1947, с. 141.
- ↑ Обрядовый бубен «Сокол», Бубен с оленем
- ↑ Bonner, 2017, с. 529.
- ↑ Nielsen, 2010, с. 75.
- ↑ Вёрман, 2015, с. 140.
- ↑ Grünbaum, 1994.
Литература
- Pierre Wantzel. Recherches sur les moyens de Reconnaître si un Problème de géométrie peau se résoudre avec la règle et le compas // Journal de Mathématiques. — 1837. — С. 366–372.
- Andrew Mattei Gleason. Angle trisection, the heptagon // The American Mathematical Monthly. — 1988. — Март (вып. 3). — С. 185–194. — DOI:10.2307/2323624.
- W. W. Rose Ball, H. S. M.Coxeter. Mathematical recreations and Essays. — Thirteenth edition. — New York: The MacMillan company, 1947. — С. 141.
- Перевод: Математические эссе и развлечения / перевод Н.И. Плужниковой, А.С.Попова, Г.М. Цукерман, под редакцией И.М.Яглома. — Москва: «Мир», 1986. — С. 156.
- John H. Conway, Heidi Burgiel, Chaim Goodman-Strass. Chapter 20, Generalized Schaefli symbols, Types of symmetry of a polygon // The Symmetries of Things. — Chaim Goodman-Strauss, 2008. — С. 275—278. — ISBN 978-1-56881-220-5.
- Branko Grünbaum. Metamorphoses of polygons // The Lighter Side of Mathematics: Proceedings of the Eugène Strens Memorial Conference on Recreational Mathematics and its History. — 1994.
- Jay Bonner. Islamic geometric pattens. — Springer, 2017. — ISBN 978-1-4419-0216-0.
- Nielsen D. Design & Nature V: Comparing Design in Nature with Science and Engineering // Fifth international conference on comapring design in nature with science engineering / Angelo Carpi, C. A. Brebbia. — WIT Press, 2010. — ISBN 978-1-84564-454-3.
- Вёрман К. История искусств всех времен и народов. — Москва, Берлин: Директ-медиа, 2015. — Т. 3 Книга2-3. — ISBN 978-5-4475-3827-9.
Для улучшения этой статьи желательно: |
Данная страница на сайте WikiSort.ru содержит текст со страницы сайта "Википедия".
Если Вы хотите её отредактировать, то можете сделать это на странице редактирования в Википедии.
Если сделанные Вами правки не будут кем-нибудь удалены, то через несколько дней они появятся на сайте WikiSort.ru .