WikiSort.ru - Не сортированное

Построе́ния с по́мощью ци́ркуля и лине́йки — раздел евклидовой геометрии, известный с античных времён.

В задачах на построение циркуль и линейка предполагаются идеальными инструментами, в частности:

• Линейка не имеет делений и имеет сторону бесконечной длины, но только одну.
• Циркуль может иметь какой угодно большой или малый раствор (то есть может чертить окружность произвольного радиуса).

Примеры

Построение правильного шестиугольника

Задача на бисекцию. С помощью циркуля и линейки разбить данный отрезок AB на две равные части. Одно из решений показано на рисунке:

• Циркулем проводим окружности с центром в точках A и B радиусом AB.
• Находим точки пересечения P и Q двух построенных окружностей (дуг).
• По линейке проводим отрезок или линию, проходящую через точки P и Q.
• Находим искомую середину отрезка AB — точку пересечения AB и PQ.

Формальное определение

В этом разделе не хватает ссылок на источники информации. Информация должна быть проверяема, иначе она может быть поставлена под сомнение и удалена. Вы можете отредактировать эту статью, добавив ссылки на авторитетные источники. Эта отметка установлена 1 февраля 2016 года.

В задачах на построение рассматриваются множество следующих объектов: все точки плоскости, все прямые плоскости и все окружности плоскости. В условиях задачи изначально задается (считается построенными) некоторое множество объектов. К множеству построенных объектов разрешается добавлять (строить):

1. произвольную точку;
2. произвольную точку на заданной прямой;
3. произвольную точку на заданной окружности;
4. точку пересечения двух заданных прямых;
5. точки пересечения/касания заданной прямой и заданной окружности;
6. точки пересечения/касания двух заданных окружностей;
7. произвольную прямую, проходящую через заданную точку;
8. прямую, проходящую через две заданные точки;
9. произвольную окружность с центром в заданной точке;
10. произвольную окружность с радиусом, равным расстоянию между двумя заданными точками;
11. окружность с центром в заданной точке и с радиусом, равным расстоянию между двумя заданными точками.

Требуется с помощью конечного количества этих операций построить другое множество объектов, находящееся в заданном соотношении с исходным множеством.

Решение задачи на построение содержит в себе три существенные части:

1. Описание способа построения заданного множества.
2. Доказательство того, что множество, построенное описанным способом, действительно находится в заданном соотношении с исходным множеством. Обычно доказательство построения производится как обычное доказательство теоремы, опирающееся на аксиомы и другие доказанные теоремы.
3. Анализ описанного способа построения на предмет его применимости к разным вариантам начальных условий, а также на предмет единственности или неединственности решения, получаемого описанным способом.

Известные задачи

• Задача Аполлония о построении окружности, касающейся трех заданных окружностей. Если ни одна из заданных окружностей не лежит внутри другой, то эта задача имеет 8 существенно различных решений.
• Задача Брахмагупты о построении вписанного четырехугольника по четырем его сторонам.

Построение правильных многоугольников

Основная статья: Теорема Гаусса — Ванцеля

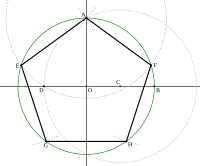
Античным геометрам были известны способы построения правильных n-угольников для ${\displaystyle n=2^{k}}$ , ${\displaystyle n=3\cdot 2^{k}}$ , ${\displaystyle n=5\cdot 2^{k}}$ и ${\displaystyle n=3\cdot 5\cdot 2^{k}}$ .

В 1796 году Гаусс показал возможность построения правильных n-угольников при ${\displaystyle n=2^{k}\cdot p_{1}\cdots p_{m}}$ , где ${\displaystyle p_{i}}$  — различные простые числа Ферма. В 1836 году Ванцель доказал, что других правильных многоугольников, которые можно построить циркулем и линейкой, не существует.

Допустимые отрезки для построения с помощью циркуля и линейки

С помощью этих инструментов возможно построение отрезка, который по длине:

1. равен сумме длин нескольких отрезков;
2. равен разности длин двух отрезков;
3. численно равен произведению длин двух отрезков;
4. численно равен частному от деления длин двух отрезков;
5. численно равен квадратному корню из длины заданного отрезка (следует из возможности построения среднего геометрического двух отрезков, см. иллюстрацию).^[4]

Для построения отрезка с длиной численно равной произведению, частному и квадратному корню из длин заданных отрезков необходимо задание на плоскости построения единичного отрезка (то есть отрезка длины 1). Извлечение корней из отрезков с иными натуральными степенями, не являющимися степенью числа 2, невозможны с помощью циркуля и линейки. Так, например, невозможно при помощи циркуля и линейки из единичного отрезка построить отрезок длиной ${\displaystyle {\sqrt[{3}]{2}}}$ . Из этого факта, в частности, следует неразрешимость задачи об удвоении куба.^[5]

Возможные и невозможные построения

С формальной точки зрения, решение любой задачи на построение сводится к графическому решению некоторого алгебраического уравнения, причем коэффициенты этого уравнения связаны с длинами заданных отрезков. Поэтому можно сказать, что задача на построение сводится к отысканию действительных корней некоторого алгебраического уравнения.

Поэтому удобно говорить о построении числа — графического решения уравнения определенного типа.

Исходя из возможных построений отрезков возможны следующие построения:

• Построение решений линейных уравнений.
• Построение решений уравнений, сводящихся к решениям квадратных уравнений.

Иначе говоря, возможно строить лишь отрезки, равные арифметическим выражениям с использованием квадратного корня из исходных чисел (заданных длин отрезков).

Важно отметить, что существенно, что решение должно выражаться при помощи квадратных корней, а не радикалов произвольной степени. Если даже алгебраическое уравнение имеет решение в радикалах, то из этого не следует возможность построения циркулем и линейкой отрезка, равного его решению. Простейшее такое уравнение: ${\displaystyle x^{3}-2=0,}$ связанное со знаменитой задачей на удвоение куба, сводящаяся к этому кубическому уравнению. Как было сказано выше, решение этого уравнения (${\displaystyle {\sqrt[{3}]{2}}}$ ) невозможно построить циркулем и линейкой.

Возможность построить правильный 17-угольник следует из выражения для косинуса центрального угла его стороны:

${\displaystyle \cos {\left({\frac {2\pi }{17}}\right)}=-{\frac {1}{16}}\;+\;{\frac {1}{16}}{\sqrt {17}}\;+\;{\frac {1}{16}}{\sqrt {34-2{\sqrt {17}}}}\;+\;}$

${\displaystyle +{\frac {1}{8}}{\sqrt {17+3{\sqrt {17}}-{\sqrt {34-2{\sqrt {17}}}}-2{\sqrt {34+2{\sqrt {17}}}}}},}$

что, в свою очередь, следует из возможности сведения уравнения вида ${\displaystyle x^{F_{n}}-1=0,}$ где ${\displaystyle F_{n}}$  — любое простое число Ферма, с помощью замены переменной к квадратному уравнению.

Вариации и обобщения

• Построения с помощью одного циркуля. По теореме Мора — Маскерони с помощью одного циркуля можно построить любую фигуру, которую можно построить циркулем и линейкой. При этом прямая считается построенной, если на ней заданы две точки.
• Построения с помощью одной линейки. Очевидно, что с помощью одной линейки можно проводить только проективно-инвариантные построения. В частности,
  • невозможно даже разбить отрезок на две равные части,
  • также невозможно найти центр данной окружности.

Однако,

• при наличии на плоскости заранее проведённой окружности с отмеченным центром с одной линейкой можно провести те же построения, что и циркулем и линейкой (теорема Штейнера — Понселе).
• Если на линейке есть две засечки, то построения с её помощью эквивалентны построениям с помощью циркуля и линейки (важный шаг в доказательстве этого сделал Наполеон).

• Построения с помощью инструментов с ограниченными возможностями. В задачах такого рода инструменты (в противоположность классической постановке задачи) считаются не идеальными, а ограниченными: прямую через две точки с помощью линейки можно провести только при условии, что расстояние между этими точками не превышает некоторой величины; радиус окружностей, проводимых с помощью циркуля, может быть ограничен сверху, снизу или одновременно и сверху, и снизу.
• Построения с помощью плоского оригами см. правила Фудзиты
• Построения с помощью шарнирных механизмов (англ.) — это построения на плоскости и в пространстве с помощью единичных стержней, связанных на концах шарнирами. Этим способом можно построить любое алгебраическое число^[6].

Интересные факты

• Центральный узор на государственном флаге Ирана законодательно описывается как построение с помощью циркуля и линейки^[7].

См. также

• Программные пакеты динамической геометрии позволяют выполнять виртуальные построения с помощью циркуля и линейки на мониторе компьютера.

Примечания

Литература

• Адлер А. Теория геометрических построений / Перевод с немецкого Г. М. Фихтенгольца. — Издание третье. — Л.: Учпедгиз, 1940. — 232 с.
• Александров И. И. Сборник геометрических задач на построение. — Издание восемнадцатое. — М.: Учпедгиз, 1950. — 176 с.
• Аргунов Б. И., Балк М. Б. Геометрические построения на плоскости. Пособие для студентов педагогических институтов. — Издание второе. — М.: Учпедгиз, 1957. — 268 с.
• Воронец А. М. Геометрия циркуля. — М.-Л.: ОНТИ, 1934. — 40 с. — (Популярная библиотека по математике под общей редакцией Л. А. Люстерника).
• Гейлер В. А. Неразрешимые задачи на построение // СОЖ. — 1999. — № 12. — С. 115—118.
• Кириченко В. А. Построения циркулем и линейкой и теория Галуа // Летняя школа «Современная математика». — Дубна, 2005.
• Манин Ю. И. Книга IV. Геометрия // Энциклопедия элементарной математики. — М.: Физматгиз, 1963. — 568 с.
• Петерсен Ю. Методы и теории решения геометрических задач на построение. — М.: Типография Э. Лисснера и Ю. Романа, 1892. — 114 с.
• Прасолов В. В. Три классические задачи на построение. Удвоение куба, трисекция угла, квадратура круга. — М.: Наука, 1992. — 80 с. — (Популярные лекции по математике).
• Геометрические построения // Справочник по математике (для ср. уч. заведений)/ Цыпкин А.Г., под ред. Степанова С.А. — 3-е изд. — М.: Наука, Гл. редакция физ.-мат. литературы, 1983. — С. 200–213. — 480 с.
• Штейнер Я. Геометрические построения, выполняемые с помощью прямой линии и неподвижного круга. — М.: Учпедгиз, 1939. — 80 с.
• Факультативный курс по математике. 7-9 / Сост. И. Л. Никольская. — М.: Просвещение, 1991. — С. 80. — 383 с. — ISBN 5-09-001287-3.