WikiSort.ru - Не сортированное

В геометрии политоп (многогранник, многоугольник или замощение, например) изогонален или вершинно транзитивен, если, грубо говоря, все его вершины эквивалентны. Отсюда следует, что все вершины окружены одним и тем же видом граней^[en]* в том же самом (или обратном) порядке и с теми же самыми углами между соответствующими гранями.

Формально, мы говорим, что для любых двух вершин существует симметрия политопа, отображающая первую вершину изометрично во вторую. Другой путь сказать то же самое — что группа автоморфизмов политопа транзитивна на его вершинах, или что вершины лежат внутри одной орбиты симметрии.

Все вершины конечной n-мерной изогональной фигуры существуют на (n-1)-сфере.

Термин изогональный давно использовался в контексте многогранников. Термин вершинно транзитивный является синонимом, позаимствованным из современных идей групп симметрии и теории графов.

Четырёхскатный повернутый купол^[en] — не являющийся изогональным — демонстрирует, что утверждение «все вершины выглядят одинаковыми» не столь ограничительно, как определение, приведённое выше, которое вовлекает группу изометрий, сохраняющую многогранник или мозаику.

Изогональные многоугольники и бесконечноугольники

Изогональные бесконечноугольники
Изогональные пространственные бесконечноугольники[en]

Все правильные многоугольники, бесконечноугольники и правильные звёздчатые многоугольники являются изогональными. Двойственная фигура для изогонального многоугольника — изотоксальный многоугольник^[en].

Некоторые многоугольники с чётным числом сторон и бесконечноугольники, с попеременными двумя длинами сторон, например прямоугольник, являются изогональными.

Все плоские изогональные 2n-угольники имеют диэдральную симметрию (D_n, n=2,3,...) с осями симметрии через середины сторон.

D2	D3	D4	D7
Изогональные прямоугольники и скрещ1нные прямоугольники[en] имеют одно и то же расположение вершин[en]	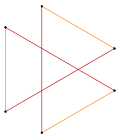Изогональная гексаграмма с 6 идентичными вершинами и двумя длинами рёбер [1]	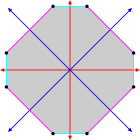Изогональный выпуклый восьмиугольник с синими и красными радиальными осями симметрии	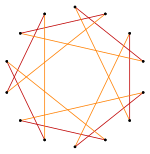Изогональный «звёздчатый» четырнадцатиугольник с одним типом вершин и двумя типами рёбер [2].

Изогональные 3-мерные многогранники и 2D-мозаики

Изогональные мозаики

Деформированная квадратная мозаика

Деформированная усечённая квадратная мозаика

Изогональный многогранник (3D) и 2D-мозаика имеют единственный вид вершин. Изогональный многогранник с правильными гранями является также однородным многогранником^[en] и может быть представлен нотацией вершинной конфигурации^[en]*, путём последовательного перечисления граней вокруг каждой вершины. Геометрически деформированные варианты однородных многогранников и мозаик могут также быть заданы вершинной конфигурацией.

Изогональные (3D) многогранники

D3d, порядок 12	Th, порядок 24	Oh[en], порядок 48
4.4.6	3.4.4.4	4.6.8	3.8.8
Деформированная шестиугольная призма	Деформированный ромбокубооктаэдр	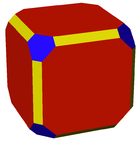Слегка усечённый кубооктаэдр	Сверхусечённый куб

Изогональные 3D-многогранники и 2D-мозаики можно классифицировать далее

• Правильный — если он также изоэдрален^[en] (транзитивен по граням) и изотоксален (рёберно транзитивен). Из этого следует, что все грани многогранника являются правильными многоугольниками одного вида.
• Квазиправильный — если он также изотоксален (рёберно транзитивен), но не изоэдрален^[en] (транзитивен по граням).
• Полуправильный — если любая грань является правильным многоугольником, но многогранник не изоэдрален^[en] (транзитивен по граням) или не изотоксален (рёберно транзитивен). (Определение полуправильного многогранника зависит от автора. Некоторые авторы исключают тела с диэдральной симметрией или невыпуклые тела.)
• Однородный^[en] — если любая грань является правильным многоугольником, т.е. многогранник правильный, семиправильный или полуправильный.
• Благородный^[en] — если он также изоэдрален^[en] (транзитивен по граням).

Размерность N(> 3) — изогональные многогранники и мозаики

Определения изогональных фигур могут быть распространены на многогранники более высоких размерностей и соты. В общем случае все однородные многогранники^[en] являются изогональными, например, однородные 4-мерные многогранники^[en] и выпуклые однородные соты^[en].

Двойственный многогранник для изогонального многогранника является изотопическим^[en], т.е. транзитивен по фасетам.

k-изогональные и k-однородные фигуры

Многогранник или соты называются k-изогональными, если его вершины образуют k классов транзитивности. Более ограничивающий термин, k-однородный определяется как k-изогональная фигура, состоящая только из правильных многоугольников. Они могут быть представлены визуально различными цветами однородной раскраски^[en].

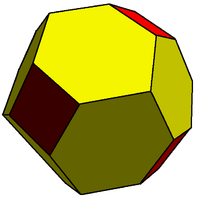Этот усечённый робмододекаэдр[en] является 2-изогональным, поскольку он содержит два класса транзитивности вершин. Этот многогранник состоит из квадратов и сплюснутых шестиугольников.

Эта полуправильная мозаика является также 2-изогональной (и 2-однородной). Эта мозаика состоит из правильных треугольных и правильных шестиугольных граней.

2-изогональная 9/4 эннеаграмма

См. также

• Рёберно-транзитивная фигура^[en] (изотоксальная фигура)
• Транзитивная по граням фигура^[en] (изоэдральная фигура)

Примечания

Литература

• Grünbaum, Branko.  The Lighter Side of Mathematics: Proceedings of the Eugène Strens Memorial Conference on Recreational Mathematics and its History / Ed. by Richard K. Guy, Robert E. Woodrow. — The Mathematical Association of America, 1996. Figure 1. Parameter t=2.0
• Coxeter H. S. M.  The densities of the regular polytopes, Part II // Math. Proc. Cambridge Philos. Soc. — 1931. — P. 509—521.
• Cromwell, Peter R.  Polyhedra. — Cambridge University Press, 1997. — P. 369 Transitivity. — ISBN 0-521-55432-2.
• Grünbaum B., Shephard G. C.  Tilings and Patterns. — W. H. Freeman and Company, 1987. — ISBN 0-7167-1193-1. (p. 33 k-isogonal tiling; p. 65 k-uniform tilings)

Ссылки

• Weisstein, Eric W. Vertex-transitive graph (англ.) на сайте Wolfram MathWorld.
• George Olshevsky Transitivity Glossary for Hyperspace. Archived from the original on 4 February 2007.
• George Olshevsky Glossary for Hyperspace. Archived from the original on 4 February 2007.
• Isogonal Kaleidoscopical Polyhedra Vladimir L. Bulatov, Physics Department, Oregon State University, Corvallis, Presented at Mosaic2000, Millennial Open Symposium on the Arts and Interdisciplinary Computing, 21–24 August 2000, Seattle, WA VRML models
• Steven Dutch uses the term k-uniform for enumerating k-isogonal tilings
• List of n-uniform tilings
• Weisstein, Eric W. Demiregular tessellations (англ.) на сайте Wolfram MathWorld. (Also uses term k-uniform for k-isogonal)

Для улучшения этой статьи желательно: Проверить качество перевода с иностранного языка. Исправить статью согласно стилистическим правилам Википедии.