WikiSort.ru - Не сортированное

Равнобедренный прямоугольный треугольник — это треугольник, являющийся одновременно равнобедренным и прямоугольным. В этом треугольнике каждый внутренний угол равен 45°:

${\displaystyle \alpha =\beta =45^{\circ }={\frac {\pi }{4}}\!\,,}$

третий внутренний угол — прямой:

${\displaystyle \gamma =180^{\circ }-2\alpha =90^{\circ }={\frac {\pi }{2}}\!\,,}$

Внутренние углы имеют соотношение 1 : 1 : 2.

Каждая боковая сторона равна:

${\displaystyle a=b={\frac {c{\sqrt {2}}}{2}}\!\,,}$

а основание равно:

${\displaystyle c=a{\sqrt {2}}\!\,,}$

стороны соотносятся как 1 : 1 : √2. Боковые стороны являются катетами, основание — гипотенузой.

Высота, опущенная на гипотенузу, равна её половине:

${\displaystyle v_{c}={\frac {a{\sqrt {2}}}{2}}={\frac {c}{2}}=R\!\,,}$

где R — радиус описанной окружности.

Периметр

Периметр равнобедренного прямоугольного треугольника равен

${\displaystyle P=a+b+c=a(2+{\sqrt {2}})\!\,.}$

Площадь

Площадь равнобедренного прямоугольного треугольника равна

${\displaystyle S={\frac {a^{2}}{2}}={\frac {c^{2}}{4}}\!\,.}$

Также площадь равнобедренного прямоугольного треугольника можно выразить при помощи формулы Герона:

${\displaystyle S={\sqrt {p(p-a)^{2}(p-a{\sqrt {2}})}}\!\,,}$

де p — полупериметр равнобедренного прямоугольного треугольника:

${\displaystyle p={\frac {P}{2}}=a\left(1+{\frac {\sqrt {2}}{2}}\right)\!\,.}$

Общие характеристики

Описанная и вписанная окружности

Равнобедренный прямоугольный треугольник, как и все треугольники, является бицентрическим. В нём:

${\displaystyle r\!\,}$	${\displaystyle R\!\,}$	${\displaystyle a\!\,}$	${\displaystyle c\!\,}$
${\displaystyle R\left({\sqrt {2}}-1\right)={\frac {a}{2}}\left(2-{\sqrt {2}}\right)={\frac {c}{2}}\left({\sqrt {2}}-1\right)\!\,}$	${\displaystyle {\frac {r}{{\sqrt {2}}-1}}={\frac {a}{2}}{\sqrt {2}}={\frac {c}{2}}\!\,}$	${\displaystyle {\frac {2r}{2-{\sqrt {2}}}}=R{\sqrt {2}}={\frac {c}{2}}{\sqrt {2}}\!\,}$	${\displaystyle {\frac {2r}{{\sqrt {2}}-1}}=2R=a{\sqrt {2}}\!\,}$

Здесь r — радиус вписанной окружности, R — радиус описанной окружности, a — катеты и c — гипотенуза треугольника.

Расстояние между центрами вписанной и вписанной окружности d равен радиусу вписанной окружности r и задается уравнением Эйлера:

${\displaystyle d^{2}=R(R-2r)={\frac {a^{2}}{2}}\left(3-2{\sqrt {2}}\right)\!\,}$

${\displaystyle d=r={\frac {a}{2}}\left(2-{\sqrt {2}}\right)=a{\sqrt {{\frac {1}{2}}\left(3-2{\sqrt {2}}\right)}}\approx 0,2928932\,a\!\,.}$

Равнобедренный треугольник, имеющий равные описанную и вписанную окружность и одинаковые расстояния между их центрами (${\displaystyle d=r\,}$ ), имеет углы:

${\displaystyle \alpha =\beta =\operatorname {arc\,tg} {\frac {4-{\sqrt {2}}}{{\sqrt {2}}{\sqrt {8{\sqrt {2}}-11}}}}\approx 72,968751^{\circ }\!\,,}$

${\displaystyle \gamma =180^{\circ }-2\alpha \approx 34,062496^{\circ }\!\,.}$

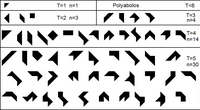
Полиформы в головоломках

Полиформы, основными фигурами которых являются равнобедренные прямоугольные треугольники, - это поляболы.

Пять равнобедренных прямоугольных треугольников вместе с одним квадратом и одним параллелограммом образуют головоломку пазл.

В этой статье не хватает ссылок на источники информации. Информация должна быть проверяема, иначе она может быть поставлена под сомнение и удалена. Вы можете отредактировать эту статью, добавив ссылки на авторитетные источники. Эта отметка установлена 4 августа 2018 года.