
Высота треугольника — перпендикуляр, опущенный из вершины треугольника на противоположную сторону (точнее, на прямую, содержащую противоположную сторону). В зависимости от типа треугольника высота может содержаться внутри треугольника (для остроугольного треугольника), совпадать с его стороной (являться катетом прямоугольного треугольника) или проходить вне треугольника у тупоугольного треугольника.
Свойства точки пересечения трех высот треугольника (ортоцентра)
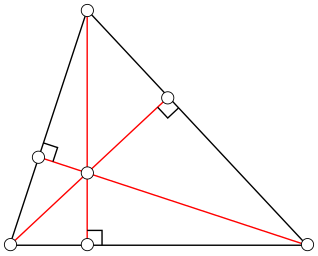
- Все три высоты треугольника пересекаются в одной точке, называемой ортоцентром. Это утверждение легко доказать, используя векторное тождество, справедливое для любых точек , не обязательно даже лежащих в одной плоскости:
(Для доказательства тождества следует воспользоваться формулами
В качестве точки E следует взять пересечение двух высот треугольника.)
- Последнее утверждение также является следствием теорем о вершинах подерного треугольника (прямой и обратной) [1]
- Ортоцентр изогонально сопряжен центру описанной окружности.
- Ортоцентр лежит на одной прямой с центроидом, центром описанной окружности и центром окружности девяти точек (см. прямая Эйлера).
- Ортоцентр остроугольного треугольника является центром окружности, вписанной в его ортотреугольник.
- Центр описанной около треугольника окружности служит ортоцентром треугольника с вершинами в серединах сторон данного треугольника. Последний треугольник называют дополнительным треугольником по отношению к первому треугольнику.
- Последнее свойство можно сформулировать так: Центр описанной около треугольника окружности служит ортоцентром дополнительного треугольника.
- Точки, симметричные ортоцентру треугольника относительно его сторон, лежат на описанной окружности.
- Точки, симметричные ортоцентру треугольника относительно середин сторон, также лежат на описанной окружности и совпадают с точками, диаметрально противоположными соответствующим вершинам.
- Если О — центр описанной окружности ΔABC, то
,
- , где — радиус описанной окружности; — длины сторон треугольника.
- Расстояние от вершины треугольника до ортоцентра вдвое больше, чем расстояние от центра описанной окружности до противоположной стороны.
- Любой отрезок, проведенный из ортоцентра до пересечения с описанной окружностью всегда делится окружностью Эйлера пополам. Ортоцентр есть центр гомотетии этих двух окружностей.
- Теорема Гамильтона. Три отрезка прямых, соединяющих ортоцентр с вершинами остроугольного треугольника, разбивают его на три треугольника, имеющих ту же самую окружность Эйлера (окружность девяти точек), что и исходный остроугольный треугольник.
- Следствия теоремы Гамильтона:
- Три отрезка прямых, соединяющих ортоцентр с вершинами остроугольного треугольника, разбивают его на три треугольника Гамильтона, имеющих равные радиусы описанных окружностей.
- Радиусы описанных окружностей трёх треугольников Гамильтона равны радиусу окружности, описанной около исходного остроугольного треугольника.
- В остроугольном треугольнике ортоцентр лежит внутри треугольника; в тупоугольном — вне треугольника; в прямоугольном — в вершине прямого угла.
Свойства высот равнобедренного треугольника
- Если в треугольнике две высоты равны, то треугольник — равнобедренный (теорема Штейнера — Лемуса), и третья высота одновременно является медианой и биссектрисой того угла, из которого она выходит.
- Верно и обратное: в равнобедренном треугольнике две высоты равны, а третья высота одновременно является медианой и биссектрисой.
- У равностороннего треугольника все три высоты равны.
Свойства оснований высот треугольника
- Основания высот образуют так называемый ортотреугольник, обладающий собственными свойствами.
- Описанная около ортотреугольника окружность - окружность Эйлера. На этой окружности также лежат три середины сторон треугольника и три середины трёх отрезков, соединяющих ортоцентр с вершинами треугольника.
- Другая формулировка последнего свойства:
- Теорема Эйлера для окружности девяти точек. Основания трёх высот произвольного треугольника, середины трёх его сторон (основания его внутренних медиан) и середины трёх отрезков, соединяющих его вершины с ортоцентром, все лежат на одной окружности (на окружности девяти точек).
- Теорема. В любом треугольнике отрезок, соединяющий основания двух высот треугольника, отсекает треугольник подобный данному.
- Теорема. В треугольнике отрезок, соединяющий основания двух высот треугольника, лежащие на двух сторонах, антипараллелен третьей стороне, с которой он не имеет общих точек. Через два его конца, а также через две вершины третьей упомянутой стороны всегда можно провести окружность.
Другие свойства высот треугольника
- Если треугольник разносторонний (неравносторонний), то его внутренняя биссектриса, проведённая из любой вершины, лежит между внутренними медианой и высотой, проведёнными из той же вершины.
- Высота треугольника изогонально сопряжена диаметру (радиусу) описанной окружности, проведенному из той же самой вершины.
- В остроугольном треугольнике две его высоты отсекают от него подобные треугольники.
- В прямоугольном треугольнике высота, проведенная из вершины прямого угла, разбивает его на два треугольника, подобных исходному.
Свойства минимальной из высот треугольника
Минимальная из высот треугольника обладает многими экстремальными свойствами. Например:
- Минимальная ортогональная проекция треугольника на прямые, лежащие в плоскости треугольника, имеет длину, равную наименьшей из его высот.
- Минимальный прямолинейный разрез в плоскости, через который можно протащить несгибаемую треугольную пластину, должен иметь длину, равную наименьшей из высот этой пластины.
- При непрерывном движении двух точек по периметру треугольника друг навстречу другу, максимальное расстояние между ними за время движения от первой встречи до второй, не может быть меньше длины наименьшей из высот треугольника.
- Минимальная высота в треугольнике всегда проходит внутри этого треугольника.
Основные соотношения
- где — площадь треугольника, — длина стороны треугольника, на которую опущена высота.
- где - произведение боковых сторон, радиус описанной окружности
- , где — радиус вписанной окружности.
- , где — площадь треугольника.
- , — сторона треугольника к которой опускается высота .
- Высота равнобедренного треугольника, опущенная на основание:
- где — основание, — боковая сторона.
- — высота в равностороннем треугольнике со стороной .
Теорема о высоте прямоугольного треугольника
Если высота в прямоугольном треугольнике длиной , проведённая из вершины прямого угла, делит гипотенузу длиной на отрезки и , соответствующие катетам и , то верны следующие равенства:
- ;
Теорема о проекциях
См. с. 51, ф. (1.11-4)[2]. Теорема о проекциях: . Из теоремы о проекциях следует то, что высота, опущенная, например, из вершины , делит противоположную ей сторону на две части и , считая от вершины к .
Мнемоническое стихотворение
Высота похожа на кота,
Который, выгнув спину,
И под прямым углом
Соединит вершину
И сторону хвостом.[3]
Вариации по теме. Высоты в четырехугольнике
Теорема[4]. Пусть – вписанный четырёхугольник, – основание перпендикуляра (высоты), опущенного из вершины на диагональ ; аналогично определяются точки . Тогда точки лежат на одной окружности.
Примечания
- ↑ Зетель С.И. Новая геометрия треугольника. Пособие для учителей. 2-е издание.. — М.: Учпедгиз, 1962. — С. 137-138, п. 126, теорема, следствия.
- ↑ Корн Г.А., Корн Т.М. Справочник по математике для научных работников и инженеров. — М.: «Наука», 1974. — 832 с.
- ↑ Сафронова Вера Николаевна,. Урок геометрии в 7-м классе по теме: "Медиана, биссектриса, высота". Открытый урок. Издательский дом «Первое сентября». Проверено 19 июля 2017.
- ↑ Вокруг задачи Архимеда. Упр. 7, рис. 11, следствие, c. 5.
Ссылки
Данная страница на сайте WikiSort.ru содержит текст со страницы сайта "Википедия".
Если Вы хотите её отредактировать, то можете сделать это на странице редактирования в Википедии.
Если сделанные Вами правки не будут кем-нибудь удалены, то через несколько дней они появятся на сайте WikiSort.ru .











































