Те́нзор (от лат. tensus, «напряженный») — объект линейной алгебры, линейно преобразующий элементы одного линейного пространства в элементы другого. Частными случаями тензоров являются скаляры, векторы, билинейные формы и т. п.

Часто тензор представляют как многомерную таблицу , заполненную числами — компонентами тензора (где — размерность векторного пространства, над которым задан тензор, а число сомножителей совпадает с т. н. валентностью или рангом тензора). Такие таблицы, в случае двумерного массива (тензор ранга 2), на письме отображают матричной записью:
Важно, что такое представление (кроме тензоров валентности ноль — скаляров) возможно только после выбора базиса (или системы координат): при смене базиса компоненты тензора меняются определённым образом.
Сам тензор как «геометрическая сущность» от выбора базиса не зависит, что можно наглядно видеть на примере вектора, являющегося частным случаем тензора: компоненты вектора меняются при смене координатных осей, но сам вектор — образом которого может быть просто направленный отрезок — от этого не изменяется.
Координаты тензора обычно обозначают некоторой буквой с совокупностью верхних (контрвариантных) и нижних (ковариантных) индексов: . При смене базиса ковариантные компоненты меняются так же, как и базис (с помощью того же преобразования), а контравариантные — обратно изменению базиса (обратным преобразованием).
Термин «тензор» также часто служит сокращением для термина «тензорное поле», изучением которых занимается тензорное исчисление.
Пример

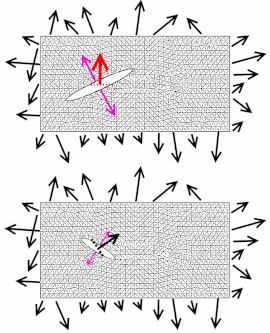
Простейшей иллюстрацией, позволяющей понять физический (и отчасти геометрический) смысл тензоров, а более точно — симметричных тензоров второго ранга, будет, вероятно, рассмотрение тензора отрезка ткани под внешней нагрузкой (см. рис. А). Нагрузкой для куска ткани может служить растяжение её руками в разные стороны, или натягивание ткани на какую-то сложную форму.
Интуитивно понятно, что в разных точках ткани напряжение будет разным, например, из-за формы и ориентации молекул, атомных слоёв или разного плетения. Для описания состояния напряжения в различных точках ткани и используются тензоры. Другими словами, каждой точке ткани соответствует свой математический объект — тензор . Это похоже на то, как любой точке пространства может соответствовать своя температура или давление воздуха.
Чтобы понять как тензор показывает состояние напряжения в какой-нибудь точке ткани, можно сделать маленький разрез в данной точке и понаблюдать в каком направлении будут расходится данные разрезы (направление роста разрыва в ткани обозначено фиолетовыми векторами ). Так на рис. А мы сделали два разреза в разных точках ткани: направление одного разреза показано красной пунктирной линией, направление другого — синей пунктирной линией. Чтобы математически описать направление данных разрезов используется вектор нормали (вектор перпендикулярный плоскости разреза). Так у разреза вектор нормали красный и направлен перпендикулярно плоскости разреза, у разреза ситуация похожая.
Как видно разрезы были сделаны в одном направлении, но ткань отозвалась тем, что разрез начал расти в совершенно другом направлении. Для предсказания того, куда будет развиваться разрез как раз и используется тензор напряжений. Математически данное предсказание выглядело бы так:
- Определить "тензорную функцию" , аргументами которой являются координаты точек внутри тела, а значением является тензор, описывающий состояние напряжения в заданной точке тела.
- Выбрать точку в теле, например, и из получить тензор, который описывает состояние напряжения в точке
- Определить направление плоскости , в которой будет проводится разрез тела.
- Умножить направление разреза в точке на тензор напряжения в данной точке , что в математической записи выглядит как
- Вектор и покажет, куда будет распространяться разрез в точке .
Разрезы и — это вектора, а напряжение в точке — это тензор.
Следует понимать, что разнонаправленные разрезы, совершённые в одной и той же точке тела, повлекут за собой различный отклик ткани. Данное явление показано на рис. Б, где разрастание разрыва ткани происходит по разным направлениям и с разной интенсивностью , в ответ на различные направления первоначальных разрезов и , совершённых в одной и той же точке.
Как раз для описания такого сложного поведения и используются тензоры, которые в данном случае служат векторными функциями , определёнными в каждой точке куска ткани, которые ставят все возможные направления разрезов в соответствие со всеми возможными направлениями дальнейшего разрыва ткани.
Представление тензора в матричном виде
Чтобы представить вышеописанный тензор (тензор второго ранга) не в функциональном (операторном) виде, например, , а в матричном , сначала нужно выбрать базис, относительно которого будут высчитываться «координаты тензора»

Очевидно, что с физической точки зрения, поведение ткани никак не зависит от математической точки зрения — выбора системы координат. То есть, какой бы базис ни выбрал наблюдатель, он никак не может повлиять на то, как ткань отзывается на разрезы в её теле.
Явление независимости тензора от выбора базиса, в котором он будет представлен в по компонентном виде, напоминает явление амбиграммы, где 3-х мерный физический объект может иметь различные двумерные тени. Так на рис. В изображён сложный 3D объект, имеющий три различные (в зависимости от угла обзора) тени: , и . Чтобы построить аналогию между этим геометрическим объектом и тензором составим таблицу:
| невидимые для исследователя предметы | способы ощупывания невидимых предметов | видимые представления предмета | закон преобразования представлений |
|---|---|---|---|
| амбиграмма — сложная геометрическая форма (центр рис.В) | свет от красного, зелёного и синего фонарика | двумерные тени в форме букв , и | сама форма 3D объекта амбиграммы говорит как связаны между собой её тени |
| — тензор | «красный», «зелёный», «синий» базис | набор матриц | закон преобразования координат говорит как различные представления тензора (матрицы) могут быть связаны: |
Другими словами, матрицу можно представить как математическую тень физического объекта — тензора — в каком-то выбранном базисе. Если выбрать другой базис («математический угол зрения» на тензор ), то и матрица будет другой (то есть компоненты матрицы будут другими).
Важно понимать, тензор не просто массив чисел. Как тензор не является матрицей, так 3D объект (амбиграмма) в центре рис. В не является тенью. Наоборот, 2D тени дают представление двумерным существам, о том как может выглядеть непостижимый для них 3D объект.
Следует помнить, что не только тензор не является матрицей, но и обратно — «не всякая матрица есть тензор». Тензор лишь иногда записывают в матричной форме, но иногда матричная форма неудобна и избыточна. Таким образом, матрица является лишь одним из способов записи тензора, а не самим математическим объектом — тензором.
Также следует понимать, что не всякий линейный оператор является тензором.
Тензор отличается от других математических объектов, которые также могут быть записаны в матричной форме тем, что кроме самой матрицы для определения тензора нужно ещё задать закон преобразования координат между различными базисами.
Например, пусть для матричного представления мы выбрали «зелёный базис» и получили матрицу (зелёная тень на рис.В)
тогда, для полного задания тензора необходимо ещё указать, каким образом компоненты «зелёной матрицы» можно преобразовать в компоненты «красной» и «синей» матрицы (матричные представления того же тензора , но в других базисах).
Другими словами для задания тензора кроме самой матрицы, нужно ещё дать закон преобразования координат. Отсюда можно дать такое псевдоопределение тензора:
|
тензор = массив компонент + закон преобразования компонент при замене базиса |
Определения
Тензор определяется как геометрический объект, который описывается многомерным массивом, то есть набором чисел, занумерованных несколькими индексами, или, иначе говоря, -мерной таблицей, где — валентность тензора (см. выше).
Так, вектор (тензор первого ранга) задаётся одномерным массивом, либо в виде строки , либо в виде столбца
а такие объекты, как линейный оператор и квадратичная форма, — двумерной матрицей
Скаляр же (тензор нулевого ранга) задаётся одним числом , которое можно рассматривать как сокращённую запись нульмерного массива с единственным элементом, то есть . Такие нульмерные матрицы удобно рассматривать в качестве частных случаев тензоров, так как все тензорные определения и теоремы для них в силе, и векторы со скалярами можно при общем рассмотрении не упоминать отдельно.
Современное определение
Тензор ранга над -мерным векторным пространством — это элемент тензорного произведения пространств и сопряжённых пространств (то есть пространств линейных функционалов (ковекторов) на )
Сумма чисел называется валентностью тензора (её также часто называют рангом). Тензор ранга также называется раз контравариантным и раз ковариантным, иногда говорят тензор n-ранга, имея в виду ранг (0, n) или (n, 0), например, — тензор 3-го ранга (3 индекса).
Тензор как полилинейная функция
Точно так же, как тензор ранга можно представлять как линейный функционал на пространстве , тензор ранга удобно представлять себе как функцию от векторных аргументов , которая линейна по каждому аргументу (такие функции называются полилинейными), то есть для любой константы из поля (над которым определено векторное пространство).
В том же ключе, тензор произвольного ранга представляется полилинейным функционалом от векторов и ковекторов:
Компоненты тензора
Значения чисел в массиве, или компоненты тензора, зависят от системы координат, но при этом сам тензор как геометрическая сущность от них не зависит.
Под проявлениями этой геометрической сущности можно понимать много что:
- различные скалярные инварианты
- симметричность или антисимметричность индексов
- соотношения между тензорами
- и другое.
Например, скалярное произведение и длина векторов не меняются при поворотах осей, а метрический тензор всегда остаётся симметричным.
Свёртки любых тензоров с самими собой и/или другими тензорами (в том числе векторами), если в результате не осталось ни одного индекса, являются скалярами, то есть инвариантами относительно замены координат: это общий способ построения скалярных инвариантов.
При замене системы координат компоненты тензора преобразуются по определённому линейному закону.
Зная компоненты тензора в одной координатной системе, всегда можно вычислить его компоненты в другой, если задана матрица преобразования координат. Таким образом, второй подход можно суммировать в виде формулы:
Следует заметить, что при этом подразумевается, что все тензоры (все тензоры над одним векторным пространством), независимо от их ранга (то есть и векторы в том числе), преобразуются через одну и ту же матрицу преобразования координат (и дуальную ей, если есть верхние и нижние индексы). Компоненты тензора, таким образом, преобразуются по тому же закону, что и соответствующие компоненты тензорного произведения векторов (в количестве, равном валентности тензора), учитывая ковариантность-контравариантность компонент.
Например, компоненты тензора
преобразуются так же, как компоненты тензорного произведения трёх векторов, то есть как произведение компонент этих векторов
Так как преобразование компонент вектора известно, то таким образом можно легко сформулировать простейший из вариантов классического определения тензора.
Представление тензора в компонентах базиса
Выберем в пространстве базис , и соответственно — дуальный базис в сопряжённом пространстве (то есть , где — символ Кронекера).
Тогда в пространстве тензоров естественным образом возникает базис
- .
Произвольный тензор можно записать как линейную комбинацию базисных тензорных произведений:
Используя соглашение Эйнштейна, это разложение можно записать как
Числа называются компонентами тензора . Нижние индексы компонент тензора называются ковариантными, а верхние — контравариантными. Например, разложение некоторого дважды ковариантного тензора будет таким:
Если определить тензор как полилинейную функцию, то его компоненты определяются значениями этой функции на базисе :
Примеры
- Тензор ранга есть скаляр;
- Тензор ранга есть вектор (точнее — контравариантный вектор) — это элемент пространства , которое изоморфно пространству ;
- Тензор ранга есть ковектор (ковариантный вектор), то есть элемент пространства ;
- Тензор ранга есть билинейная форма, например, метрический тензор на касательном пространстве.
- Тензор ранга
есть линейный оператор
или
- В частности, единичный оператор, который может быть представлен единичной матрицей , — тензор ранга .
- Форма объёма на -мерном линейном пространстве есть пример антисимметрического тензора ранга (или раз ковариантного)
- Риманова кривизна в естественном виде — пример тензора ранга , её свёртки — тензор Риччи и скалярная кривизна — примеры тензоров соответственно ранга и , то есть последний — скаляр.
- Символ Леви-Чивиты — тензор 3-го ранга .
Как следует из определения, компоненты тензора должны меняться определённым образом синхронно с компонентами векторов того пространства, на котором он определён, при преобразовании координат. Поэтому не любая табличка или величина с индексами, выглядящая как представление тензора, на самом деле представляет тензор.
- Простым, хотя в целом несколько искусственным, примером такой таблички, не представляющей тензор, может быть табличка, компоненты которой представляют набор произвольных чисел, никак не меняющихся при произвольных преобразованиях координат. Такой объект не представляет тензора, или, во всяком случае, не представляет тензора на линейном пространстве, в котором произошло преобразование координат. Так, набор из трёх чисел не представляет трёхмерного вектора, если эти числа не преобразуются при замене координат совершенно определённым образом.
- Также в общем случае подмножество компонент тензора высшего ранга не является тензором низшего ранга.
- Не представляет тензора также объект, все компоненты которого нули хотя бы в одной невырожденной системе координат (в полном базисе), тогда как в другой хотя бы одна компонента ненулевая. Этот факт — следствие (поли-)линейности тензоров.
Существуют объекты, которые не только похожи на тензоры, но для которых определены (и имеют разумный и корректный смысл) тензорные операции (свёртка с другими тензорами, в частности, с векторами), однако при этом тензорами не являющиеся:
- Прежде всего, к тензорам не относятся сами матрицы преобразования координат (матрицы Якоби), являющегося частным случаем диффеоморфизма между двумя многообразиями, с помощью которых и вводится классическое определение тензора, хотя по многим своим свойствам они напоминают тензор. Для них также можно ввести верхние и нижние индексы, операции умножения, сложения и свёртки. Однако, в отличие от тензора, компоненты которого зависят лишь от координат на заданном многообразии, компоненты матрицы Якоби также зависят от координат на многообразии-образе. Это различие очевидно в том случае, когда рассматриваются матрицы Якоби диффеоморфизма двух произвольных многообразий, однако при отображении многообразия в себя его можно не заметить, так как касательные пространства образа и прообраза изоморфны (не канонически). Тем не менее, оно сохраняется. Аналогию между матрицами Якоби и тензорами можно развить, если рассматривать произвольные векторные расслоения над многообразием и их произведения, а не только касательное и кокасательное расслоение.
- Символы Кристоффеля также не представляют тензора, хотя бы потому, что они могут быть обращены в ноль выбором координат вблизи произвольной точки, так же, как выбором (криволинейных) координат могут быть сделаны ненулевыми. Однако свёртка компонент связности с вектором даёт настоящий вектор, а их разность — настоящий тензор (тензор кручения). Символы Кристоффеля, как и любые коэффициенты связности на расслоении, являются элементами более сложного пространства, чем пространство тензоров — расслоения струй.
Тензорные операции
Тензоры допускают следующие алгебраические операции:
- Умножение на скаляр — умножение каждого компонента тензора на скаляр. Аналогично умножению вектора или скалярной величины (и то, и другое являются частными случаями тензора);
- Сложение тензоров одинаковой валентности и состава индексов (вычислять сумму можно покомпонентно, как и для векторов);
- Наличие умножения на скаляр и сложения тензоров делают пространство тензоров одного и того же типа линейным пространством.
- Тензорное произведение — без ограничений. Произведением тензора ранга на тензор ранга является тензор суммарного ранга , то есть если и то их произведение
- Компоненты тензорного произведения суть произведения соответствующих компонент множителей, например:
- Свёртка тензора — специфическая тензорная операция, понижающая валентность тензора, вычисляется суммированием по паре индексов (верхнего и нижнего, если они различаются) и пробегающих, оставаясь равными друг другу, все свои значения, например:
- (последнее в эйнштейновских обозначениях, где суммирование по повторяющемуся верхнему и нижнему индексу подразумевается автоматически). Часто, если не как правило, свёртка (то есть результат операции свёртки) обозначается той же буквой, что и тензор, к которому свёртка применена, только, конечно, с количеством индексов, на два меньшим.
- След матрицы — частный случай свёртки тензора с собой.
- Свёртка двух или нескольких тензоров (в том числе тензоров и векторов), например:
- (последнее — в записи Эйнштейна).
- — операция, которую можно свести к последовательному тензорному умножению этих тензоров (см. чуть ниже) и затем свёртке получившегося тензора (возможно, несколько раз). Очевидно, эта операция линейна по всем входным каналам. Таким образом, свёртка с тензором реализует линейное или полилинейное отображение пространств тензоров на пространство тензоров (в общем случае — на другое), в частности, векторов на векторы и векторов на скаляры.
- Свёртка вектора с тензором валентности два есть действие линейного оператора, определяемого этим тензором, на вектор:
- (последнее — в записи Эйнштейна).
- Свёртка (однократная) двух тензоров валентности два реализует композицию линейных операторов, определяемых этими тензорами:
- (последнее — в записи Эйнштейна).
- Симметризация и антисимметризация — конструирование тензора того же типа с определённым видом симметрии. Для примера, симметризация тензора — это симметричный тензор , а антисимметризация — антисимметричный тензор . В общем случае симметризация по индексам имеет вид
- а антисимметризация:
- Здесь
— всевозможные перестановки индексов
а
— чётность перестановки
Разумеется, не обязательно симметризовать тензор по всем индексам, здесь это используется лишь для упрощения записи.
- Если симметричен по то симметризация по этим индексам совпадает с а антисимметризация даёт нулевой тензор. Аналогично в случае антисимметричности по некоторым индексам.
- Если то Здесь — симметричное, а — внешнее произведение векторных пространств.
Симметрии
В различного рода приложениях часто возникают тензоры с определённым свойством симметрии.
Симметричным по двум ко-(контра-)вариантным индексам называется тензор, который удовлетворяет следующему требованию:
или в компонентах
Аналогично определяется косая симметрия (или антисимметричность):
или в компонентах
Симметрия или антисимметрия не обязательно должна охватывать только соседние индексы, она может включать в себя любые индексы, учитывая, правда, следующее: симметрия или антисимметрия может относиться только к индексам одного сорта: ко- или контравариантным. Симметрии же, смешивающие ко- и контравариантные индексы тензоров, как правило, не имеют особого смысла, так как, даже если они наблюдаются в компонентах, то разрушаются при переходе к другому базису отнесения (то есть неинвариантны).
Впрочем, в присутствии метрического тензора, наличие операций поднятия или опускания индекса устраняет это неудобство, и ограничение этим по сути снимается, когда тензор представлен подходящим образом (так, например, тензор кривизны Римана антисимметричен по первым двум и последним двум индексам).
Эти определения естественным образом обобщаются на случай более чем двух индексов. При этом при любой перестановке индексов, по которым тензор является симметричным, его действие не изменяется, а при антисимметрии по индексам знак действия тензора изменяется на противоположный для нечётных перестановок (получаемых из начального расположения индексов нечётным числом транспозиций — перестановок двух индексов) и сохраняется для чётных.
Существуют и более сложные симметрии, например первое тождество Бьянки для тензора кривизны.
Тензоры в физике
В физике тензоры широко используются в теориях, обладающих геометрической природой (таких, как Общая теория относительности) или допускающих полную или значительную геометризацию (к таковым можно в значительной степени отнести практически все современные фундаментальные теории — электродинамика, релятивистская механика и т. д.), а также в теории анизотропных сред (которые могут быть анизотропны изначально, как кристаллы низкой симметрии, или вследствие своего движения или напряжений, как текущая жидкость или газ, или как деформированное твёрдое тело). Кроме того, тензоры широко используются в механике абсолютно твердого тела.
Линейные операторы квантовой механики, конечно, также могут быть интерпретированы как тензоры над некими абстрактными пространствами (пространствами состояний), но традиционно такое применение термина тензор практически не используется, как и вообще крайне редко используется для описания линейных операторов над бесконечномерными пространствами. Вообще в физике термин тензор имеет тенденцию применяться только к тензорам над обычным физическим 3-мерным пространством или 4-мерным пространством-временем, или, в крайнем случае, над наиболее простыми и прямыми обобщениями этих пространств, хотя принципиальная возможность применения его в более общих случаях остаётся.
Примерами тензоров в физике являются:
- метрический тензор над псевдоримановым 4-мерным многообразием, являющийся в ОТО развитием понятия ньютоновского гравитационного потенциала.
- выражающийся через него тензор Римановой кривизны и его свёртки, связанные в этой же теории с энергией гравитационного поля и непосредственно входящие в основное уравнение теории.
- тензор электромагнитного поля над пространством Минковского, содержащий напряжённости электрического и магнитного поля и являющийся главным объектом классической электродинамики в 4-мерной записи. В частности, уравнения Максвелла записываются с его помощью в виде единственного 4-мерного уравнения.
- напряжения и деформации в теории упругости описываются тензорами над 3-мерным евклидовым пространством. То же касается таких величин, как модули упругости.
- едва ли не большинство величин, являющихся скалярными характеристиками вещества в случае изотропности последнего, являются тензорами в случае анизотропного вещества. Говоря конкретнее, это относится к субстанциальным коэффициентам, связывающим векторные величины или стоящие перед произведениями (в частности, квадратами) векторов. Примерами могут быть удельная электропроводность (также и обратное ей удельное сопротивление), теплопроводность, диэлектрическая восприимчивость и диэлектрическая проницаемость, скорость звука (зависящая от направления) и т. д.
- в механике абсолютно твёрдого тела важнейшую роль играет тензор инерции, связывающий угловую скорость с моментом импульса и кинетической энергией вращения. Этот тензор отличается от большинства других тензоров в физике, представляющих собой, вообще говоря, тензорные поля, тем, что один тензор характеризует одно абсолютно твёрдое тело, полностью определяя, вместе с массой, его инерцию.
- аналогичным свойством обладают тензоры, входящие в мультипольное разложение: всего один тензор целиком представляет момент распределения зарядов соответствующего порядка в данное время.
- часто в физике полезен псевдотензор Леви-Чивиты, входящий, например, в координатную запись векторного и смешанного произведений векторов. Компоненты этого тензора всегда записываются практически одинаково (с точностью до скалярного множителя, зависящего от метрики), а в правом ортонормированном базисе — совершенно одинаково всегда (каждая равна 0, +1 или −1).
- термин 4-тензор — применяется для обозначения любого тензора над четырёхмерным пространством-временем, повороты системы отсчёта в котором включают как обычные повороты трёхмерного пространства, так и переход между системами отсчёта, которые движутся с разными скоростями одна относительно другой. Это тензор над пространством 4-векторов, тензор, каждый индекс которого принимает четыре значения: одно «временно́е» и три «пространственных».
Нетрудно заметить, что большинство тензоров в физике (не рассматривая скаляров и векторов) имеют всего два индекса. Тензоры, имеющие большую валентность (такие, как тензор Римана в ОТО) встречаются, как правило, только в теориях, считающихся достаточно сложными, да и то нередко фигурируют в основном в виде своих свёрток меньшей валентности. Большинство симметрично или антисимметрично.
Девиатор и шаровая часть
Любой тензор второго ранга может быть представлен в виде суммы девиатора и шаровой части:
- , .
Здесь - собственные значения тензора. Собственные значения девиатора связаны с собственными значениями тензора: . Понятие девиатора широко применяется в механике сплошных сред.[1]
См. также
Примечания
- ↑ Климов Д. М., Петров А. Г., Георгиевский Д. В. Вязкопластические течения: динамический хаос, устойчивость, перемешивание. - М., Наука, 2005. - c. 21 - ISBN 5-02-032945-2
Литература
- Акивис М. А., Гольдберг В. В. Тензорное исчисление. — М.: Наука, 1969;
- Димитриенко Ю. И. Тензорное исчисление: Учеб. пособие. — М.: Высшая школа, 2001. — 576 с. ISBN 5-06-004155-7.
- Коренев Г. В. Тензорное исчисление: Учеб. пособие. — М.: Издательство МФТИ, 2000. — 240 с. — ISBN 5-89155-047-4.
- Кочин Н. Е. Векторное исчисление и начала тензорного исчисления (9-е издание). — М.: Наука, 1965;
- Мак-Коннел А. Дж. Введение в тензорный анализ с приложениями к геометрии, механике и физике. — М.: Физматлит, 1963;
- Номидзу К. Группы Ли и дифференциальная геометрия. — М.: ИЛ, 1960;
- Победря Б. Е. Лекции по тензорному анализу: Учеб. пособие. (3-е изд.). — М.: Изд-во МГУ, 1986;
- Рашевский П. К. Риманова геометрия и тензорный анализ (3-е издание). — М.: Наука, 1967;
- Шарипов Р. А. Быстрое введение в тензорный анализ. — БашГУ.
Данная страница на сайте WikiSort.ru содержит текст со страницы сайта "Википедия".
Если Вы хотите её отредактировать, то можете сделать это на странице редактирования в Википедии.
Если сделанные Вами правки не будут кем-нибудь удалены, то через несколько дней они появятся на сайте WikiSort.ru .









































































































![\scriptstyle T_{[ij]} = {1\over 2}\left(T_{ij}-T_{ji}\right)](https://wikimedia.org/api/rest_v1/media/math/render/svg/29dd00af72830bf8d2dd8c196a3e8b48669a46fe)

![T_{[i_1\ldots i_n]} = {1\over n!}\sum_{\sigma} \mathrm{sign}\,(\sigma) T_{\sigma(i_1)\ldots \sigma(i_n)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ec6f1fcd3020ee0710a2852707f3d63ce44f61ca)









![T_{[ij]} \in V \wedge V.](https://wikimedia.org/api/rest_v1/media/math/render/svg/1c09407e682021ea86ba2a19d9b8b6e91324019c)

















