WikiSort.ru - Не сортированное

Биссектри́са (от лат. bi- «двойное», и sectio «разрезание») угла — луч, исходящий из вершины угла и делящий угол на два равных угла^[1]. Можно также определить биссектрису как геометрическое место точек внутри угла, равноудалённых от сторон этого угла.

Биссектрисой треугольника называется отрезок биссектрисы угла, проведенный от вершины угла до её пересечения с противолежащей стороной. У треугольника существуют три биссектрисы, соответствующие трём его вершинам.

Замечание

• В любом треугольнике ${\displaystyle ABC}$ , кроме внутренней или просто биссектри́сы, можно провести и внешние биссектри́сы, то есть биссектрисы углов, смежных с внутренними углами треугольника. При этом внутренняя и внешняя биссектриса одного и того же угла перпендикулярны.
• Проведение в данном треугольнике всех трёх его внешних биссектри́с до их точек пересечения друг с другом в центрах вневписанных окружностей (соответственно ${\displaystyle J_{A},J_{B},J_{C}}$ ) образует новый треугольник (см. рис.) — треугольник трёх внешних биссектрис. Это — новый треугольник центров вневписанных окружностей с вершинами ${\displaystyle J_{A},J_{B},J_{C}}$ , которые касаются соответственно сторон ${\displaystyle a,b,c}$ исходного треугольника.
• Центр окружности, проходящей через центры вневписанных окружностей — точка Бевэна.
• Исходный треугольник является ортотреугольником для треугольника ${\displaystyle \Delta J_{A}J_{B}J_{C}}$
• Точка пересечения симедиан треугольника, образованного центрами его вневписанных окружностей ${\displaystyle J_{A},J_{B},J_{C}}$ , является центром эллипса МандАра. Эту точку называют по-английски middlespoint, по-немецки — «Mittelpunkt». Она открыта в 1836-ом году Христианом Генрихом фон Нагелем (Christian Heinrich von Nagel).^[2][3]

Свойства

Свойства оснований биссектрис

• Точка пересечения биссектрисы со стороной треугольника называется основанием биссектрисы.

• Теорема о биссектрисе (см. рис.): Биссектриса внутреннего угла треугольника делит противоположную сторону (то есть делит своим основанием противоположную сторону) в отношении, равном отношению двух прилежащих сторон. То есть ${\displaystyle {\frac {BD}{CD}}={\frac {AB}{AC}}}$ или ${\displaystyle {\frac {BD}{AB}}={\frac {CD}{AC}}}$ .
• Теорема о биссектрисе — частный случай теоремы Штейнера.
• Основания биссектрис двух внутренних и одного внешнего углов треугольника лежат на одной прямой, если биссектриса внешнего угла не параллельна противоположной стороне треугольника (Одна и только одна биссектриса внешнего угла треугольника может быть параллельна противоположной стороне — основанию, если треугольник равнобедренный. У равностороннего треугольника все три биссектрисы внешних углов параллельны противоположным сторонам. Других возможностей нет).
• Биссектриса внутреннего угла треугольника делит противоположную сторону изотомически по отношению к антибиссектрисе того же угла.
• Окружности, построенные, как на диаметре, на отрезке, соединяющем основания внутренней и внешней биссектрисы, выпущенных из одного угла, проходят через точки Аполлония.
• Через точку Фейербаха проходит окружность, проведённая через основания биссектрис .^[4]

Длина биссектрис в треугольнике

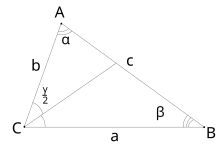
Для выведения нижеприведённых формул можно воспользоваться теоремой Стюарта.

${\displaystyle l_{c}={{\sqrt {ab(a+b+c)(a+b-c)}} \over {a+b}}={\frac {2{\sqrt {abp(p-c)}}}{a+b}}}$ , где ${\displaystyle p}$  — полупериметр.

${\displaystyle l_{c}={\sqrt {ab-a_{l}b_{l}}}}$

${\displaystyle l_{c}={\frac {2ab\cos {\frac {\gamma }{2}}}{a+b}}}$

${\displaystyle l_{c}={\frac {h_{c}}{\cos {\frac {\alpha -\beta }{2}}}}}$

Для трёх биссектрис углов ${\displaystyle A}$ , ${\displaystyle B}$ и ${\displaystyle C}$ с длинами соответственно ${\displaystyle l_{a},l_{b},}$ и ${\displaystyle l_{c}}$ , справедлива формула^[8]

${\displaystyle {\frac {(b+c)^{2}}{bc}}l_{a}^{2}+{\frac {(c+a)^{2}}{ca}}l_{b}^{2}+{\frac {(a+b)^{2}}{ab}}l_{c}^{2}=(a+b+c)^{2}.}$ ,

${\displaystyle w_{c}^{2}=a_{w}\cdot b_{w}-ab=CE^{2}=BE\cdot AE-ab}$ ,

• Инцентр (точка пересечения трёх внутренних биссектрис треугольника) делит внутреннюю биссектрису угла ${\displaystyle A}$ в отношении ${\displaystyle {\frac {b+c}{a}}}$ , где ${\displaystyle a}$ , ${\displaystyle b}$ , ${\displaystyle c}$  — стороны треугольника,

где:

• ${\displaystyle a,b,c}$  — стороны треугольника против вершин ${\displaystyle A,B,C}$ соответственно,
• ${\displaystyle \alpha ,\beta ,\gamma }$  — внутренние углы треугольника при вершинах ${\displaystyle A,B,C}$ соответственно,
• ${\displaystyle h_{c}}$  — высота треугольника, опущенная на сторону ${\displaystyle c}$ .
• ${\displaystyle l_{c}}$  — длина внутренней биссектрисы, проведённой к стороне ${\displaystyle c}$ ,
• ${\displaystyle a_{l},b_{l}}$  — длины отрезков, на которые внутренняя биссектриса ${\displaystyle l_{c}}$ делит сторону ${\displaystyle c}$ ,
• ${\displaystyle w_{c}}$  — длина внешней биссектрисы, проведённой из вершины ${\displaystyle C}$ к продолжению стороны ${\displaystyle AB}$ .
• ${\displaystyle a_{w},b_{w}}$  — длины отрезков, на которые внешняя биссектриса ${\displaystyle w_{c}}$ делит сторону ${\displaystyle c=AB}$ и её продолжение до основания самой биссектрисы.
• Если медиана ${\displaystyle m}$ , высота ${\displaystyle h}$ и внутренняя биссектриса ${\displaystyle t}$ выходят из одной и той же вершины треугольника, около которого описана окружность радиуса ${\displaystyle R}$ , тогда^{[9]:p.122,#96}

${\displaystyle 4R^{2}h^{2}(t^{2}-h^{2})=t^{4}(m^{2}-h^{2}).}$

Длина частей биссектрис в треугольнике

• Расстояние от вершины C до центра вписанной окружности равно ${\displaystyle l_{c0}={\frac {r}{\sin({\frac {\gamma }{2}})}}={\sqrt {(p-c)^{2}+r^{2}}}={\sqrt {ab-4Rr}}}$ , где R и r — радиусы описанной и вписанной окружностей, а γ — угол вершины C.
• Формулы последнего пункта по сути дают длину части биссектрисы от вершины до точки их пересечения (до центра вписанной окружности или до инцентра).
• Эту формулу и формулу для второй части внутренней биссектрисы можно также найти на основе следующего факта:
• Инцентр делит внутреннюю биссектрису угла ${\displaystyle A}$ в отношении ${\displaystyle {\frac {b+c}{a}}}$ , где ${\displaystyle a}$ , ${\displaystyle b}$ , ${\displaystyle c}$  — стороны треугольника.

Уравнения биссектрис

• Если две смежные стороны треугольника записаны уравнениями ${\displaystyle y_{1}=a_{1}x+b_{1}}$ и ${\displaystyle y_{2}=a_{2}x+b_{2}}$ , то в явном виде биссектрисы представимы в виде функций []:

${\displaystyle y={\frac {a_{1}{\sqrt {a_{2}^{2}+1}}\pm a_{2}{\sqrt {a_{1}^{2}+1}}}{{\sqrt {a_{2}^{2}+1}}\pm {\sqrt {a_{1}^{2}+1}}}}\,x+{\frac {b_{1}{\sqrt {a_{2}^{2}+1}}\pm b_{2}{\sqrt {a_{1}^{2}+1}}}{{\sqrt {a_{2}^{2}+1}}\pm {\sqrt {a_{1}^{2}+1}}}}}$

Мнемоническое правило (шуточное)

• Биссектриса — это крыса, которая бегает по углам и делит угол пополам.

См. также

• Антибиссектриса
• Высота (геометрия)
• Высота треугольника
• Инцентр
• Медиана
• Медиана треугольника
• Симедиана
• Теорема о биссектрисе
• Ось внешних биссектрис или антиортовая ось
• Треугольник
• Треугольник трёх внешних биссектрис
• Центроид
• Чевиана

Примечания

Литература

	биссектриса в Викисловаре
	Биссектриса на Викискладе

• Коган Б. Ю. Приложение механики к геометрии. — М.: Наука, 1965. — 56 с.
• Понарин Я. П. Элементарная геометрия. В 2 т. — М.: МЦНМО, 2004. — С. 30-31. — ISBN 5-94057-170-0.