WikiSort.ru - Не сортированное

Преобразование данных — это применение детерминированной математической функции к каждой точке множества данных, то есть каждая точка данных z_i заменяется преобразованным значением ${\displaystyle y_{i}=f(z_{i})}$ , где f — функция. Преобразования обычно применяются так, что данные больше подходят для процедуры статистического вывода, которую хотят применять, для улучшения интерпретируемости или для графического^[en] представления.

Почти всегда функция, которая применяется для преобразования данных, обратима, и обычно является непрерывной. Преобразование обычно применяется к коллекции сравнимых показателей. Например, если мы работаем с данными по доходам людей в некоторой валюте, обычно преобразуется доход каждого человека с помощью логарифмической функции.

Мотивировка

Руководство, как данные следует преобразовать или следует ли их вообще преобразовывать, должно проистекать из конкретного статистического анализа. Например, простой путь для построения примерно 95 % доверительного интервала для математического ожидания популяции — взять среднее арифметическое плюс-минус две стандартные ошибки. Однако постоянный множитель 2, используемый здесь, относится к нормальному распределению и применим, только если среднее арифметическое варьируется примерно по нормальному закону. Центральная предельная теорема утверждает, что во многих ситуациях среднее арифметическое не варьируется по нормальному закону, если размер выборки достаточно велик. Однако, если совокупность существенно асимметрична, а размер выборки умеренный, аппроксимация, даваемая центральной предельной теоремой, может быть плохой, а получающийся доверительный интервал, скорее всего, будет иметь неверный уровень доверия^[en]. Тогда, в случае, когда имеется доказательство о существенной асимметрии данных, обычно данные преобразуются к симметричному распределению перед построением доверительного интервала. Если есть необходимость, доверительный интервал может быть преобразован обратно к исходному масштабу, используя обратное к используемому для преобразования данных.

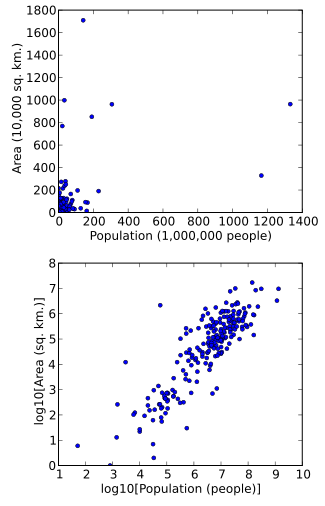
Данные могут быть также преобразованы для облегчения визуализации. Например, предположим, что мы имеем диаграмму рассеяния, в которой точками являются страны мира, а значения данных, отражённые на графике, отражают площадь и популяцию каждой страны. Если график сделан из непреобразованных данных (например, квадратных километров для площади и число людей в популяции), большинство стран окажутся в плотном кластере в нижнем левом углу графика. Некоторые страны с очень большой площадью и/или популяцией будут распределены жидко по основной площади графика. Простое масштабирование единиц (например, к тысячам квадратных километров или к миллионам людей) не меняет ситуацию. Однако при логарифмическом преобразовании как площади, так и популяции, точки будут распределены на графе более равномерно.

Последней причиной преобразования данных может быть улучшение интерпретируемости, даже если не предполагается никакого формального статистического анализа или визуализации. Например, предположим, что мы сравниваем автомобили в терминах их экономии топлива. Эти данные обычно представляются как «километров на литр» или «миль на галлон». Однако, если целью является определение, сколько дополнительного топлива на человека нужно использовать в год, если использовать один автомобиль по сравнению с другим, более естественно работать с данными, преобразованными с помощью функции 1/x, которая даёт литры на километр или галлоны на милю.

В регрессии

Линейная регрессия — это статистическая техника для связи зависимой переменной Y с более-менее независимыми переменными X. Простейшие модели регрессии выявляют линейную связь между математическим ожиданием Y и каждой независимой переменной (если другие независимые переменные фиксированы). Если линейность не выполняется, даже приближённо, иногда можно преобразовать либо независимые переменные, либо зависимые переменные в регрессионной модели для улучшения линейности.

Другое предположение линейной регрессии — что дисперсия одна и та же для любого возможного математического ожидания (что известно как гомоскедастичность). Одномерная нормальность не нужна, чтобы оценка методом наименьших квадратов параметров регрессии имела смысл (см. статью «Теорема Гаусса — Маркова»). Однако доверительные интервалы и проверка гипотез будут иметь лучшие статистические свойства, если переменные обладают многомерной номальностью. Это можно получить эмпирически путём графического представления значений по отношению к невязкам^[en] и рассмотрения графика нормальных квантилей^[en] невязок. Заметим, неважно, зависимая переменная Y нормально распределена или нет.

Примеры

Уравнение: ${\displaystyle Y=a+bX}$

Значение: Единичное увеличение X связано в среднем с увеличением в b раз значения Y.

Равенство: ${\displaystyle \log(Y)=a+bX}$      (Получается взятием логарифма от обоих частей равенства ${\displaystyle Y=e^{a}e^{bX}}$ )

Значение: Единичное увеличение X связано в среднем с увеличением на b% значения Y.

Равенство: ${\displaystyle Y=a+b\log(X)}$

Значение: Увеличение на 1% X связано в среднем с увеличением в b/100 раз значения Y.

Равенство: ${\displaystyle \log(Y)=a+b\log(X)}$      (Получается взятием логарифма от обоих частей равенства ${\displaystyle Y=e^{a}X^{b}}$ )

Значение: Увеличение на 1% X связано в среднем с увеличением на b% значения Y.

Общие случаи

Логарифмические преобразования и преобразования к квадратному корню обычно используются для положительных данных, а преобразование к противоположному по умножению (1/x) может быть использовано для ненулевых данных. Степенное преобразование^[en] является семейством преобразований, параметризованным неотрицательным значением λ, в это семейство входят логарифмическое преобразование, преобразование к квадратному корню и преобразование к обратному значению (1/x) в качестве специальных случаев. Чтобы получить преобразование данных целенаправленно, можно использовать технику статистической оценки для оценки параметра λ в степенном преобразовании, тем самым определяя преобразование, которое наиболее пригодно при заданных условиях. Поскольку семейство степенных преобразований включает также тождественное преобразование, этот подход может также показывать, не лучше ли анализировать данные без преобразования. В регрессионном анализе эта техника известна как техника Бокса-Кокса.

Преобразование к противоположному значению (1/x) и некоторые степенные преобразования могут быть с успехом применено к данным, которые содержат как положительные, так и отрицательные значения (степенное преобразование обратимо для всех вещественных чисел, если λ является нечётным целым числом). Однако, если наблюдаются как положительные, так и отрицательные значения, обычно начинают с добавления ко всем значениям константы для получения набора неотрицательных чисел, к которым можно затем применять любое степенное преобразование. Обычная ситуация, когда преобразование данных применяется, — это когда разброс рассматриваемых значений составляет несколько порядков. Многие физические и социальные явления проявляют такое поведение — доходы, размер популяции, размеры галактик и количество осадков как примеры. Степенное преобразование и, в частности, логарифм, может быть часто использовано для достижения симметрии в таких данных. Логарифм часто предпочтительнее, поскольку легче интерпретировать его результаты в терминах «кратности изменений».

Логарифм имеет также полезное свойство на дробях. Если мы сравниваем положительные значения X и Y используя отношения X / Y, то в случае X < Y отношение попадает на единичный отрезок (0,1), а когда X > Y, отношение попадает на полуось (1,∞), а равенство отношения 1 соответствует равенству величин. В анализе, когда X и Y трактуются симметрично, логарифм отношения log(X / Y) равен нулю в случае равенства и присутствует свойство, что в случае, когда X в K раз больше Y, логарифм отношения одинаково отстоит от нуля от случая, когда Y в K раз больше X (логарифм отношения в этих ситуациях равен log(K) и −log(K)).

Если значения изначально лежат между 0 и 1, не включая граничные значения, то может оказаться подходящим преобразование logit — оно даёт значения в диапазоне (−∞,∞).

Преобразования для многомерных статистик

Одномерные функции могут быть применены поточечно к многомерным данным для изменения их частных распределений. Возможно также изменение некоторых свойств многомерных распределений с помощью подходящим образом построенных преобразований. Например, при работе с временными рядами и другими типами последовательных данных обычно переходят к конечным разностям данных для улучшения стационарности. Если данные, образованные случайным вектором X, наблюдаются как вектора X_i наблюдения с ковариационной матрицей Σ, может быть использовано линейное отображение для устранения корреляции данных. Чтобы сделать это, используется разложение Холецкого для получения Σ = A A'. Тогда преобразованный вектор ${\displaystyle Y_{i}=A^{-1}X_{i}}$ имеет единичную матрицу в качестве ковариационной матрицы.

См. также

• Степенное преобразование^[en] (Метод Бокса-Кокса)
• Logit
• Arcsin (преобразование, например, для коэффициента корреляции Пирсона)

Примечания

Литература

Ссылки

• Log transformation
• Transformations, means, and confidence intervals
• Log Transformations for Skewed and Wide Distributions – обсуждаются логарифмическое и «знаковое логарифмическое» преобразования (Глава из «Practical Data Science with R»).

Для улучшения этой статьи желательно: Проверить качество перевода с иностранного языка. Исправить статью согласно стилистическим правилам Википедии.