WikiSort.ru - Не сортированное

Существует много связей между однородными многогранниками^[en]. Построение Витхоффа способно построить почти все однородные многогранники из треугольников Шварца. Числа, которые могут быть использованы для сторон недиэдрического треугольника Шварца, которые не обязательно приводят только к вырожденным многогранникам, равны 2, 3, 3/2, 4, 4/3, 5, 5/2, 5/3 и 5/4 (но числа с числителями 4 и 5 не могут встречаться вместе). Число 4/2 тоже можно использовать, но оно приводит к вырожденным однородным многогранникам, поскольку 4 и 2 имеют общий делитель. Существует 44 таких треугольников Шварца (5 с тетраэдральной симметрией, 7 с октаэдральной симметрией^[en] и 32 с икосаэдральной симметрией^[en]), которые, вместе с бесконечным семейством диэдрических треугольников Шварца, могут образовать почти все невырожденные однородные многогранники. Многие вырожденные однородные многогранники с полностью совпадающими вершинами, рёбрами или гранями могут быть также сгенерированы с помощью построения Витхоффа, и те, которые возникают из треугольников Шварца, не использующих 4/2, также включены в таблицы ниже вместе с их невырожденными аналогами.

Существует несколько невитхоффовых однородных многогранника, которые треугольники Шварца не могут сгенерировать. Однако большинство из них может быть получено с помощью построения Витхоффа как двойное покрытие (невитхоффов многогранник покрывается дважды) или с несколькими дополнительными гранями (см. Всеусечённый многогранник^[en]). Такие многогранники помечены в списке звёздочкой. Только для двух однородных многогранников построение Витхоффа не работает — это Большой биромбоикосододекаэдр^[en] и Большой биплосконосый биромбобидодекаэдр^[en].

Каждая мозаика треугольников Шварца на сфере может покрыть сферу только раз, либо, вместо этого, обойти сферу кратное число раз, пересекая себя в процессе покрытия. Число раз, которые мозаика оборачивает сферу, является плотностью^[en] мозаики и обозначается μ.

Для экономии места в статье используются короткие имена многогранников, данные Джонатаном Бауэрсом (Jonathan Bowers), и известные как сокращения (акронимы) Бауэрса. Номер Маедера (система «Mathematic»^[1]^[2]) также дан. За исключением диэдрических треугольников Шварца, треугольники Шварца упорядочены по их плотности.

Треугольники Мёбиуса и Шварца

Согласно книге Коксетера (Коксетер, «Uniform polyhedra»^[3]), существует 4 сферических треугольника с углами π/p, π/q, π/r, где (p q r) — целые числа:

(2 2 r) — Диэдральный
(2 3 3) — Тетраэдраьный
(2 3 4) — Октаэдральный
(2 3 5) — Икосаэдральный

Они называются треугольниками Мёбиуса.

В треугольнике Шварца кроме этих троек допускаются (p q r) с рациональными числами.

Плотность (μ)	Треугольники
1	(2 3 3)	(2 3 4)	(2 3 5)
d	(2 2 n/d)
2	(3/2 3 3)	(3/2 4 4)	(3/2 5 5)	(5/2 3 3)
3	(2 3/2 3)	(2 5/2 5)
4	(3 4/3 4)	(3 5/3 5)
5	(2 3/2 3/2)	(2 3/2 4)
6	(3/2 3/2 3/2)	(5/2 5/2 5/2)	(3/2 3 5)	(5/4 5 5)
7	(2 3 4/3)	(2 3 5/2)
8	(3/2 5/2 5)
9	(2 5/3 5)
10	(3 5/3 5/2)	(3 5/4 5)
11	(2 3/2 4/3)	(2 3/2 5)
13	(2 3 5/3)
14	(3/2 4/3 4/3)	(3/2 5/2 5/2)	(3 3 5/4)
16	(3 5/4 5/2)
17	(2 3/2 5/2)
18	(3/2 3 5/3)	(5/3 5/3 5/2)
19	(2 3 5/4)
21	(2 5/4 5/2)
22	(3/2 3/2 5/2)
23	(2 3/2 5/3)
26	(3/2 5/3 5/3)
27	(2 5/4 5/3)
29	(2 3/2 5/4)
32	(3/2 5/4 5/3)
34	(3/2 3/2 5/4)
38	(3/2 5/4 5/4)
42	(5/4 5/4 5/4)

Сводная таблица

Существует семь генерирующих точек в каждом наборе p, q, r (и несколько специальных случаев):

Общий случай				Прямоугольный треугольник (r=2)
Описание	Символ Витхоффа	Конфигурация вершины	Диаграмма Коксетера	Символ Витхоффа	Конфигурация вершины	Символ Шлефли	Диаграмма Коксетера
правильный и квазиправильный	q \| p r	(p.r)^q		q \| p 2	p^q	{p,q}
	p \| q r	(q.r)^p		p \| q 2	q^p	{q,p}
	r \| p q	(q.p)^r		2 \| p q	(q.p)²	t₁{p,q}
усечённый и растянутый	q r \| p	q.2p.r.2p		q 2 \| p	q.2p.2p	t_0,1{p,q}
	p r \| q	p.2q.r.2q		p 2 \| q	p.2q.2q	t_0,1{q,p}
	p q \| r	2r.q.2r.p		p q \| 2	4.q.4.p	t_0,2{p,q}
с чётным числом граней	p q r \|	2r.2q.2p		p q 2 \|	4.2q.2p	t_0,1,2{p,q}
с чётным числом граней	p q r s \|	2p.2q.-2p.-2q	-	p 2 r s \|	2p.4.-2p.⁴/₃		-
плосконосый^[en]	\| p q r	3.r.3.q.3.p		\| p q 2	3.3.q.3.p	sr{p,q}
плосконосый^[en]	\| p q r s	(4.p.4.q.4.r.4.s)/2	-	-	-		-

Существует четыре специальных случая:

p q r
s | — Смесь p q r | и p q s |. Оба символа p q r | и p q s | образуют общий базовый многогранник с некоторыми дополнительными гранями. Запись p q r
s | тогда представляет базовый многогранник, сделанный из общих граней p q r | и p q s |.
| p q r — Плосконосые формы (альтернированные).
| p q r s — Единственная плосконосая форма для U75^[en], который не получается из построения Витхоффа с использованием треугольной фундаментальной области. В этот символ Витхоффа входят четыре числа, поскольку имеет четырёхугольную сферичесую фундаментаьную область.
| (p) q (r) s — Единственная плосконосая форма для фигуры Скиллинга^[en], которую нельзя получить построением Витхоффа.

Эта таблица преобразования символа Витхоффа в конфигурацию вершины не работает для некоторых исключительных однородных многогранников. Единственными невырожденными такими случаями являются большой усечённый кубооктаэдр^[en] (2 3 4/3 |), усечённый додекододекаэдр^[en] (2 5/3 5 |), Большой икосаэдр (| 2 3/2 3/2), большой вывернутый обратноплосконосый икосододекаэдр (| 2 3/2 5/3) и малый плосконосый икосоикосододекаэдр^[en] (| 3/2 3/2 5/2). В этих случаях вершинная фигура является крайне деформированной для того, чтобы получить однородность с плоскими гранями — в первых двух случаях это тупоугольный треугольник, а не остроугольный, а в последних трёх случаях это пентаграмма или гексаграмма вместо пятиугольника или шестиугольника, и они оборачиваются вокруг центра дважды. Это приводит к тому, что часть граней проходят сквозь многогранник и выходят с другой стороны многогранника. По этой же причине плотность многогранника не совпадает с плотностью треугольника Шварца, из которого они получены, и равны 1, 3, 7, 37 и 38 соответственно.

Диэдральные (Призматические)

В диэдральных треугольниках Шварца два числа равны 2, а третье может быть произвольным рациональным числом, строго большим 1.

(2 2 n/d) – вырожденный, если НОД(n, d) > 1.

Много многогранников с диэдральной симметрией имеют двуугольные грани, что делает их вырожденными многогранниками (то есть диэдрами и осоэдрами). Столбцы таблицы, содержащие только вырожденные многогранники не включены — специальные вырожденные случаи (только для треугольников Шварца (2 2 2)) помечены большим крестом. Скрещенные антипризмы^[en] с третьим значением {p}, где p < 3/2 существовать не могут, поскольку их вершинные фигуры тогда нарушили бы неравенство треугольника. Эти невозможные фигуры также отмечены большим крестом. 3/2-скрещенная антипризма является вырожденной, поскольку в евклидовом пространстве она плоская, а потому тоже помечена большим крестом. Треугольники Шварца (2 2 n/d) перечислены здесь только для случаев НОД (n, d) = 1, в противном случае все полученные многогранники будут вырожденными.

Список даёт все возможные случаи для n ≤ 6.

(p q r)	p q.2p.r.2p	q p.2q.r.2q	2r.2q.2p	p q r 3.r.3.q.3.p
(2 2 2) (μ=1)	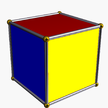X	X	4.4.4 cube 4-p	3.3.3 tet 2-ap
(2 2 3) (μ=1)	4.3.4 trip 3-p	4.3.4 trip 3-p	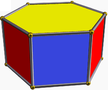6.4.4 hip 6-p	3.3.3.3 oct 3-ap
(2 2 3/2) (μ=2)	4.3.4 trip 3-p	4.3.4 trip 3-p	6/2.4.4 2trip 6/2-p	X
(2 2 4) (μ=1)	4.4.4 cube 4-p	4.4.4 cube 4-p	8.4.4 op 8-p	3.4.3.3 squap 4-ap
(2 2 4/3) (μ=3)	4.4.4 cube 4-p	4.4.4 cube 4-p	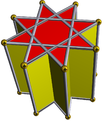8/3.4.4 stop 8/3-p^[en]	X
(2 2 5) (μ=1)	4.5.4 pip 5-p	4.5.4 pip 5-p	10.4.4 dip 10-p	3.5.3.3 pap 5-ap
(2 2 5/2) (μ=2)	4.5/2.4 stip 5/2-p	4.5/2.4 stip 5/2-p	10/2.4.4 2pip 10/2-p	3.5/2.3.3 stap 5/2-ap^[en]
(2 2 5/3) (μ=3)	4.5/2.4 stip 5/2-p	4.5/2.4 stip 5/2-p	10/3.4.4 stiddip 10/3-p^[en]	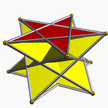3.5/3.3.3 starp 5/3-ap^[en]
(2 2 5/4) (μ=4)	4.5.4 pip 5-p	4.5.4 pip 5-p	10/4.4.4 – 10/4-p	X
(2 2 6) (μ=1)	4.6.4 hip 6-p	4.6.4 hip 6-p	12.4.4 twip 12-p^[en]	3.6.3.3 hap 6-ap
(2 2 6/5) (μ=5)	4.6.4 hip 6-p	4.6.4 hip 6-p	12/5.4.4 stwip 12/5-p^[en]	X
(2 2 n) (μ=1)	4.n.4 n-p	4.n.4 n-p	2n.4.4 2n-p	3.n.3.3 n-ap
(2 2 n/d) (μ=d)	4.n/d.4 n/d-p	4.n/d.4 n/d-p	2n/d.4.4 2n/d-p	3.n/d.3.3 n/d-ap

Тетраэдральные

В тетраэдральных треугольниках Шварца максимальный числитель не должен превосходить 3.

(3 3 2)
(3 3 3/2)
(3 2 3/2)
(2 3/2 3/2)
(3/2 3/2 3/2)

#	(p q r)	p r (p.r)^q	q r (q.r)^p	p q (q.p)^r	p q.2p.r.2p	q p.q.r.2q	r 2r.q.2r.p	2r.2q.2p	p q r 3.r.3.q.3.p
1	(3 3 2) (µ=1)	3.3.3 tet U1	3.3.3 tet U1	3.3.3.3 oct U5	3.6.6 tut U2	3.6.6 tut U2	4.3.4.3 co U7	4.6.6 toe U8	3.3.3.3.3 ike U22
2	(3 3 3/2) (µ=2)	(3.3.3.3.3.3)/2 2tet –	(3.3.3.3.3.3)/2 2tet –	(3.3.3.3.3.3)/2 2tet –	3.6.3/2.6 oho U3^[en]	3.6.3/2.6 oho U3^[en]	2(6/2.3.6/2.3) 2oct –	2(6/2.6.6) 2tut –	2(3.3/2.3.3.3.3) 2oct+8{3} –
3	(3 2 3/2) (µ=3)	3.3.3.3 oct U5	3.3.3 tet U1	3.3.3 tet U1	3.6.6 tut U2	2(3/2.4.3.4) 2thah U4*	3(3.6/2.6/2) 3tet –	2(6/2.4.6) cho+4{6/2} U15*^[en]	?
4	(2 3/2 3/2) (µ=5)	3.3.3 tet U1	3.3.3.3 oct U5	3.3.3 tet U1	3.4.3.4 co U7	3(6/2.3.6/2) 3tet –	3(6/2.3.6/2) 3tet –	4(6/2.6/2.4) 2oct+6{4} –	(3.3.3.3.3)/2 gike U53
5	(3/2 3/2 3/2) (µ=6)	(3.3.3.3.3.3)/2 2tet –	(3.3.3.3.3.3)/2 2tet –	(3.3.3.3.3.3)/2 2tet –	2(6/2.3.6/2.3) 2oct –	2(6/2.3.6/2.3) 2oct –	2(6/2.3.6/2.3) 2oct –	6(6/2.6/2.6/2) 6tet –	?

Октаэдральные

В октаэдральных треугольниках Шварца максимальным разрешённым числителем является 4. Существуют также октаэдральные треугольники с 4/2, но они дают только вырожденные однородные многогранники, поскольку 4 и 2 не взаимно просты.

(4 3 2)
(4 4 3/2)
(4 3 4/3)
(4 2 3/2)
(3 2 4/3)
(2 3/2 4/3)
(3/2 4/3 4/3)

#	(p q r)	p r (p.r)^q	q r (q.r)^p	p q (q.p)^r	p q.2p.r.2p	q p.2q.r.2q	r 2r.q.2r.p	2r.2q.2p	p q r 3.r.3.q.3.p
1	(4 3 2) (µ=1)	4.4.4 cube U6	3.3.3.3 oct U5	3.4.3.4 co U7	3.8.8 tic U9	4.6.6 toe U8	4.3.4.4 sirco U10	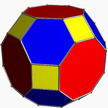4.6.8 girco U11	3.3.3.3.4 snic U12
2	(4 4 3/2) (µ=2)	(3/2.4)⁴ oct+6{4} –	(3/2.4)⁴ oct+6{4} –	(4.4.4.4.4.4)/2 2cube –	3/2.8.4.8 socco U13^[en]	3/2.8.4.8 socco U13^[en]	2(6/2.4.6/2.4) 2co –	2(6/2.8.8) 2tic –	?
3	(4 3 4/3) (µ=4)	(4.4.4.4.4.4)/2 2cube –	(3/2.4)⁴ oct+6{4} –	(3/2.4)⁴ oct+6{4} –	3/2.8.4.8 socco U13^[en]	2(4/3.6.4.6) 2cho U15*^[en]	3.8/3.4.8/3 gocco U14^[en]	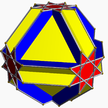6.8.8/3 cotco U16^[en]	?
4	(4 2 3/2) (µ=5)	3.4.3.4 co U7	3.3.3.3 oct U5	4.4.4 cube U6	3.8.8 tic U9	4.4.3/2.4 querco U17^[en]	4(4.6/2.6/2) 2oct+6{4} –	2(4.6/2.8) sroh+8{6/2} U18*^[en]	?
5	(3 2 4/3) (µ=7)	3.4.3.4 co U7	4.4.4 cube U6	3.3.3.3 oct U5	4.6.6 toe U8	4.4.3/2.4 querco U17^[en]	3.8/3.8/3 quith U19^[en]	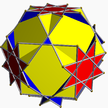4.6/5.8/3 quitco U20^[en]	?
6	(2 3/2 4/3) (µ=11)	4.4.4 cube U6	3.4.3.4 co U7	3.3.3.3 oct U5	4.3.4.4 sirco U10	4(4.6/2.6/2) 2oct+6{4} –	3.8/3.8/3 quith U19^[en]	2(4.6/2.8/3) groh+8{6/2} U21*	?
7	(3/2 4/3 4/3) (µ=14)	(3/2.4)⁴ = (3.4)⁴/3 oct+6{4} –	(4.4.4.4.4.4)/2 2cube –	(3/2.4)⁴ = (3.4)⁴/3 oct+6{4} –	2(6/2.4.6/2.4) 2co –	3.8/3.4.8/3 gocco U14^[en]	3.8/3.4.8/3 gocco U14^[en]	2(6/2.8/3.8/3) 2quith –	?

Икосаэдральные

В икосаэдральных треугольниках Шварца максимальным разрешённым числителем может быть 5. Кроме того, числитель 4 не может быть использован во всех икосаэдральных треугольниках Шварца, хотя числители 2 и 3 разрешены. (Если бы 4 и 5 могли появляться одновременно в некоторых треугольниках Шварца, они должны были бы появиться и в некоторых треугольниках Мёбиуса, но это невозможно, так как (2 4 5) является гиперболическим треугольником, а не сферическим.)

(5 3 2)
(3 3 5/2)
(5 5 3/2)
(5 5/2 2)
(5 3 5/3)
(5/2 5/2 5/2)
(5 3 3/2)
(5 5 5/4)
(3 5/2 2)
(5 5/2 3/2)
(5 2 5/3)
(3 5/2 5/3)
(5 3 5/4)
(5 2 3/2)
(3 2 5/3)
(5/2 5/2 3/2)
(3 3 5/4)
(3 5/2 5/4)
(5/2 2 3/2)
(5/2 5/3 5/3)
(3 5/3 3/2)
(3 2 5/4)
(5/2 2 5/4)
(5/2 3/2 3/2)
(2 5/3 3/2)
(5/3 5/3 3/2)
(2 5/3 5/4)
(2 3/2 5/4)
(5/3 3/2 5/4)
(3/2 3/2 5/4)
(3/2 5/4 5/4)
(5/4 5/4 5/4)

#	(p q r)	p r (p.r)^q	q r (q.r)^p	p q (q.p)^r	p q.2p.r.2p	q p.2q.r.2q	r 2r.q.2r.p	2r.2q.2p	p q r 3.r.3.q.3.p
1	(5 3 2) (µ=1)	5.5.5 doe U23	3.3.3.3.3 ike U22	3.5.3.5 id U24	3.10.10 tid U26	5.6.6 ti U25	4.3.4.5 srid U27	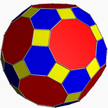4.6.10 grid U28	3.3.3.3.5 snid U29
2	(3 3 5/2) (µ=2)	3.5/2.3.5/2.3.5/2 sidtid U30^[en]	3.5/2.3.5/2.3.5/2 sidtid U30^[en]	(3¹⁰)/2 2ike –	3.6.5/2.6 siid U31^[en]	3.6.5/2.6 siid U31^[en]	2(10/2.3.10/2.3) 2id –	2(10/2.6.6) 2ti –	3.5/2.3.3.3.3 seside U32^[en]
3	(5 5 3/2) (µ=2)	(5.3/2)⁵ cid –^[en]	(5.3/2)⁵ cid –^[en]	(5.5.5.5.5.5)/2 2doe –	5.10.3/2.10 saddid U33^[en]	5.10.3/2.10 saddid U33^[en]	2(6/2.5.6/2.5) 2id –	2(6/2.10.10) 2tid –	2(3.3/2.3.5.3.5) 2id+40{3} –
4	(5 5/2 2) (µ=3)	(5.5.5.5.5)/2 gad U35	5/2.5/2.5/2.5/2.5/2 sissid U34	5/2.5.5/2.5 did U36	5/2.10.10 tigid U37^[en]	5.10/2.10/2 3doe –	4.5/2.4.5 raded U38^[en]	2(4.10/2.10) sird+12{10/2} U39*^[en]	3.3.5/2.3.5 siddid U40^[en]
5	(5 3 5/3) (µ=4)	5.5/3.5.5/3.5.5/3 ditdid U41^[en]	(3.5/3)⁵ gacid –^[en]	(3.5)⁵/3 cid –^[en]	3.10.5/3.10 sidditdid U43^[en]	5.6.5/3.6 ided U44^[en]	10/3.3.10/3.5 gidditdid U42^[en]	10/3.6.10 idtid U45^[en]	3.5/3.3.3.3.5 sided U46^[en]
6	(5/2 5/2 5/2) (µ=6)	(5/2)¹⁰/2 2sissid –	(5/2)¹⁰/2 2sissid –	(5/2)¹⁰/2 2sissid –	2(5/2.10/2)² 2did –	2(5/2.10/2)² 2did –	2(5/2.10/2)² 2did –	6(10/2.10/2.10/2) 6doe –	3(3.5/2.3.5/2.3.5/2) 3sidtid –
7	(5 3 3/2) (µ=6)	(3.5.3.5.3.5)/2 gidtid U47^[en]	(3¹⁰)/4 2gike –	(3.5.3.5.3.5)/2 gidtid U47^[en]	2(3.10.3/2.10) 2seihid U49*^[en]	5.6.3/2.6 giid U48^[en]	5(6/2.3.6/2.5) 3ike+gad –	2(6.6/2.10) siddy+20{6/2} U50*^[en]	5(3.3.3.3.3.5)/2 5ike+gad –
8	(5 5 5/4) (µ=6)	(5¹⁰)/4 2gad –	(5¹⁰)/4 2gad –	(5¹⁰)/4 2gad –	2(5.10.5/4.10) 2sidhid U51*^[en]	2(5.10.5/4.10) 2sidhid U51*^[en]	10/4.5.10/4.5 2did –	2(10/4.10.10) 2tigid –	3(3.5.3.5.3.5) 3cid –
9	(3 5/2 2) (µ=7)	(3.3.3.3.3)/2 gike U53	5/2.5/2.5/2 gissid U52	5/2.3.5/2.3 gid U54^[en]	5/2.6.6 tiggy U55^[en]	3.10/2.10/2 2gad+ike –	3(4.5/2.4.3) sicdatrid –^[en]	4.10/2.6 ri+12{10/2} U56*^[en]	3.3.5/2.3.3 gosid U57^[en]
10	(5 5/2 3/2) (µ=8)	(5.3/2)⁵ cid –^[en]	(5/3.3)⁵ gacid –^[en]	5.5/3.5.5/3.5.5/3 ditdid U41^[en]	5/3.10.3.10 sidditdid U43^[en]	5(5.10/2.3.10/2) ike+3gad –	3(6/2.5/2.6/2.5) sidtid+gidtid –	4(6/2.10/2.10) id+seihid+sidhid –	?
11	(5 2 5/3) (µ=9)	5.5/2.5.5/2 did U36	5/2.5/2.5/2.5/2.5/2 sissid U34	(5.5.5.5.5)/2 gad U35	5/2.10.10 tigid U37^[en]	3(5.4.5/3.4) cadditradid –^[en]	10/3.5.5 quit sissid U58^[en]	10/3.4.10/9 quitdid U59^[en]	3.5/3.3.3.5 isdid U60^[en]
12	(3 5/2 5/3) (µ=10)	(3.5/3)⁵ gacid –^[en]	(5/2)⁶/2 2gissid –	(5/2.3)⁵/3 gacid –^[en]	2(5/2.6.5/3.6) 2sidhei U62*^[en]	3(3.10/2.5/3.10/2) ditdid+gidtid –	10/3.5/2.10/3.3 gaddid U61^[en]	10/3.10/2.6 giddy+12{10/2} U63*^[en]	3.5/3.3.5/2.3.3 gisdid U64^[en]
13	(5 3 5/4) (µ=10)	(5.5.5.5.5.5)/2 2doe –	(3/2.5)⁵ cid –^[en]	(3.5)⁵/3 cid –^[en]	3/2.10.5.10 saddid U33^[en]	2(5.6.5/4.6) 2gidhei U65*^[en]	3(10/4.3.10/4.5) sidtid+ditdid –	2(10/4.6.10) siddy+12{10/4} U50*^[en]	?
14	(5 2 3/2) (µ=11)	5.3.5.3 id U24	3.3.3.3.3 ike U22	5.5.5 doe U23	3.10.10 tid U26	3(5/4.4.3/2.4) gicdatrid –^[en]	5(5.6/2.6/2) 2ike+gad –	2(6/2.4.10) sird+20{6/2} U39*^[en]	5(3.3.3.5.3)/2 4ike+gad –
15	(3 2 5/3) (µ=13)	3.5/2.3.5/2 gid U54^[en]	5/2.5/2.5/2 gissid U52	(3.3.3.3.3)/2 gike U53	5/2.6.6 tiggy U55^[en]	3.4.5/3.4 qrid U67^[en]	10/3.10/3.3 quit gissid U66^[en]	10/3.4.6 gaquatid U68^[en]	3.5/3.3.3.3 gisid U69^[en]
16	(5/2 5/2 3/2) (µ=14)	(5/3.3)⁵ gacid –^[en]	(5/3.3)⁵ gacid –^[en]	(5/2)⁶/2 2gissid –	3(5/3.10/2.3.10/2) ditdid+gidtid –	3(5/3.10/2.3.10/2) ditdid+gidtid –	2(6/2.5/2.6/2.5/2) 2gid –	10(6/2.10/2.10/2) 2ike+4gad –	?
17	(3 3 5/4) (µ=14)	(3.5.3.5.3.5)/2 gidtid U47^[en]	(3.5.3.5.3.5)/2 gidtid U47^[en]	(3)¹⁰/4 2gike –	3/2.6.5.6 giid U48^[en]	3/2.6.5.6 giid U48^[en]	2(10/4.3.10/4.3) 2gid –	2(10/4.6.6) 2tiggy –	?
18	(3 5/2 5/4) (µ=16)	(3/2.5)⁵ cid –^[en]	5/3.5.5/3.5.5/3.5 ditdid U41^[en]	(5/2.3)⁵/3 gacid –^[en]	5/3.6.5.6 ided U44^[en]	5(3/2.10/2.5.10/2) ike+3gad –	5(10/4.5/2.10/4.3) 3sissid+gike –	4(10/4.10/2.6) did+sidhei+gidhei –	?
19	(5/2 2 3/2) (µ=17)	3.5/2.3.5/2 gid U54^[en]	(3.3.3.3.3)/2 gike U53	5/2.5/2.5/2 gissid U52	5(10/2.3.10/2) 2gad+ike –	5/3.4.3.4 qrid U67^[en]	5(6/2.6/2.5/2) 2gike+sissid –	6(6/2.4.10/2) 2gidtid+rhom –	?
20	(5/2 5/3 5/3) (µ=18)	(5/2)¹⁰/2 2sissid –	(5/2)¹⁰/2 2sissid –	(5/2)¹⁰/2 2sissid –	2(5/2.10/2)² 2did –	2(5/2.10/3.5/3.10/3) 2gidhid U70*^[en]	2(5/2.10/3.5/3.10/3) 2gidhid U70*^[en]	2(10/3.10/3.10/2) 2quitsissid –	?
21	(3 5/3 3/2) (µ=18)	(3¹⁰)/2 2ike –	5/2.3.5/2.3.5/2.3 sidtid U30^[en]	5/2.3.5/2.3.5/2.3 sidtid U30^[en]	5/2.6.3.6 siid U31^[en]	2(3.10/3.3/2.10/3) geihid U71*^[en]	5(6/2.5/3.6/2.3) sissid+3gike –	2(6/2.10/3.6) giddy+20{6/2} U63*^[en]	?
22	(3 2 5/4) (µ=19)	3.5.3.5 id U24	5.5.5 doe U23	3.3.3.3.3 ike U22	5.6.6 ti U25	3(3/2.4.5/4.4) gicdatrid –^[en]	5(10/4.10/4.3) 2sissid+gike –	2(10/4.4.6) ri+12{10/4} U56*^[en]	?
23	(5/2 2 5/4) (µ=21)	5/2.5.5/2.5 did U36	(5.5.5.5.5)/2 gad U35	5/2.5/2.5/2.5/2.5/2 sissid U34	3(10/2.5.10/2) 3doe –	3(5/3.4.5.4) cadditradid –^[en]	3(10/4.5/2.10/4) 3gissid –	6(10/4.4.10/2) 2ditdid+rhom –	?
24	(5/2 3/2 3/2) (µ=22)	5/2.3.5/2.3.5/2.3 sidtid U30^[en]	(3¹⁰)/2 2ike –	5/2.3.5/2.3.5/2.3 sidtid U30^[en]	2(3.10/2.3.10/2) 2id –	5(5/3.6/2.3.6/2) sissid+3gike –	5(5/3.6/2.3.6/2) sissid+3gike –	10(6/2.6/2.10/2) 4ike+2gad –	(3.3.3.3.3.5/2)/2 sirsid U72^[en]
25	(2 5/3 3/2) (µ=23)	(3.3.3.3.3)/2 gike U53	5/2.3.5/2.3 gid U54^[en]	5/2.5/2.5/2 gissid U52	3(5/2.4.3.4) sicdatrid –^[en]	10/3.3.10/3 quit gissid U66^[en]	5(6/2.5/2.6/2) 2gike+sissid –	2(6/2.10/3.4) gird+20{6/2} U73*^[en]	(3.3.3.5/2.3)/2 girsid U74
26	(5/3 5/3 3/2) (µ=26)	(5/2.3)⁵/3 gacid –^[en]	(5/2.3)⁵/3 gacid –^[en]	(5/2)⁶/2 2gissid –	5/2.10/3.3.10/3 gaddid U61^[en]	5/2.10/3.3.10/3 gaddid U61^[en]	2(6/2.5/2.6/2.5/2) 2gid –	2(6/2.10/3.10/3) 2quitgissid –	?
27	(2 5/3 5/4) (µ=27)	(5.5.5.5.5)/2 gad U35	5/2.5.5/2.5 did U36	5/2.5/2.5/2.5/2.5/2 sissid U34	5/2.4.5.4 raded U38^[en]	10/3.5.10/3 quit sissid U58	3(10/4.5/2.10/4) 3gissid –	2(10/4.10/3.4) gird+12{10/4} U73*^[en]	?
28	(2 3/2 5/4) (µ=29)	5.5.5 doe U23	3.5.3.5 id U24	3.3.3.3.3 ike U22	3.4.5.4 srid U27	2(6/2.5.6/2) 2ike+gad –	5(10/4.3.10/4) 2sissid+gike –	6(10/4.6/2.4/3) 2sidtid+rhom –	?
29	(5/3 3/2 5/4) (µ=32)	5/3.5.5/3.5.5/3.5 ditdid U41^[en]	(3.5)⁵/3 cid –^[en]	(3.5/2)⁵/3 gacid –^[en]	3.10/3.5.10/3 gidditdid U42^[en]	3(5/2.6/2.5.6/2) sidtid+gidtid –	5(10/4.3.10/4.5/2) 3sissid+gike –	4(10/4.6/2.10/3) gid+geihid+gidhid –	?
30	(3/2 3/2 5/4) (µ=34)	(3.5.3.5.3.5)/2 gidtid U47^[en]	(3.5.3.5.3.5)/2 gidtid U47^[en]	(3)¹⁰/4 2gike –	5(3.6/2.5.6/2) 3ike+gad –	5(3.6/2.5.6/2) 3ike+gad –	2(10/4.3.10/4.3) 2gid –	10(10/4.6/2.6/2) 2sissid+4gike –	?
31	(3/2 5/4 5/4) (µ=38)	(3.5)⁵/3 cid –^[en]	(5.5.5.5.5.5)/2 2doe –	(3.5)⁵/3 cid –^[en]	2(5.6/2.5.6/2) 2id –	3(3.10/4.5/4.10/4) sidtid+ditdid –	3(3.10/4.5/4.10/4) sidtid+ditdid –	10(10/4.10/4.6/2) 4sissid+2gike –	5(3.3.3.5/4.3.5/4) 4ike+2gad –
32	(5/4 5/4 5/4) (µ=42)	(5)¹⁰/4 2gad –	(5)¹⁰/4 2gad –	(5)¹⁰/4 2gad –	2(5.10/4.5.10/4) 2did –	2(5.10/4.5.10/4) 2did –	2(5.10/4.5.10/4) 2did –	6(10/4.10/4.10/4) 2gissid –	3(3/2.5.3/2.5.3/2.5) 3cid –

Невитхоффовы

Геми-формы

Эти многогранники (полумногогранники^[en]) получаются как двойное покрытие с помощью построения Витхоффа. Если фигура, полученная построением Витхоффа, составлена из двух идентичных компонент, операция «геми» берёт только одну компоненту.

3/2.4.3.4 thah U4 hemi(3 3/2 \| 2)	4/3.6.4.6 cho U15^[en] hemi(4 4/3 \| 3)	5/4.10.5.10 sidhid U51^[en] hemi(5 5/4 \| 5)	5/2.6.5/3.6 sidhei U62^[en] hemi(5/2 5/3 \| 3)	5/2.10/3.5/3.10/3 gidhid U70^[en] hemi(5/2 5/3 \| 5/3)
	3/2.6.3.6 oho U3^[en] hemi(?)	3/2.10.3.10 seihid U49^[en] hemi(3 3/2 \| 5)	5.6.5/4.6 gidhei U65^[en] hemi(5 5/4 \| 3)	3.10/3.3/2.10/3 geihid U71^[en] hemi(3 3/2 \| 5/3)

Приведённые формы

Эти многогранники генерируются построением Витхоффа с лишними гранями. Если фигура генерируется с помощью построения Витхоффа как соединение двух или трёх неидентичных компонент, операция «приведения» удаляет лишние грани (которые следует указать) из фигуры, оставляя только одну компоненту.

Многогранник	Лишние грани	Многогранник	Лишние грани	Многогранник	Лишние грани
4.6.4/3.6 cho U15^[en]	4{6/2}	4.8.4/3.8/7 sroh U18^[en]	8{6/2}	4.8/3.4/3.8/5 groh U21	8{6/2}
4.10.4/3.10/9 sird U39^[en]	12{10/2}	10.6.10/9.6/5 siddy U50^[en]	20{6/2}	6.4.6/5.4/3 ri U56^[en]	12{10/2}
3/2.10.3.10 seihid U49^[en]	id + sidhid	5/4.10.5.10 sidhid U51^[en]	id + seihid	10.6.10/9.6/5 siddy U50^[en]	12{10/4}
6.10/3.6/5.10/7 giddy U63^[en]	12{10/2}	4.10/3.4/3.10/9 sird U39^[en]	20{6/2}	5.6.5/4.6 gidhei U65^[en]	did + sidhei
5/2.6.5/3.6 sidhei U62^[en]	did + gidhei	6.10/3.6/5.10/7 giddy U63^[en]	20{6/2}	6.4.6/5.4/3 ri U56^[en]	12{10/4}
4.10/3.4/3.10/7 gird U73^[en]	20{6/2}	3.10/3.3/2.10/3 geihid \|U71^[en]	gid + gidhid	5/2.10/3.5/3.10/3 gidhid U70^[en]	gid + geihid
4.10/3.4/3.10/7 gird U73^[en]	12{10/4}

Тетрагемигексаэдр (thah, U4) является также приведённой формой {3/2}-купола (обратный треугольный купол, ratricu) по {6/2}.

Другие формы

Эти два однородных многогранника нельзя получить с помощью построения Витхоффа. Это множество многогранников принято называть «невитхоффовыми». Вместо треугольной фундаментальной области витхоффовых однородных многогранников эти два имеют четырёхугольную фундаментальную область.

Многогранник Скиллинга не дан в списке Маедера, поскольку он принадлежит к экзотическим однородным многогранникам, у которых рёбра полностью совпадают. Это верно также для некоторых вырожденных многогранников, перечисленных выше, таких как малый составной икосододекаэдр^[en]. Такая интерпретация совпадающих рёбер позволяет этим фигурам оставаться биметорными (греч.: bi + methoric = два + ребро), то есть имеющими две грани на ребро. Без удвоения рёбер эти тела превратились бы в тетра-, гекса-, окта-, дека- или додекаметорные фигуры, которые обычно исключаются из списка однородных многогранников. Фигура Скиллинга является тетраметорной ^[4].

(p q r s)	p q r s (4.p.4.q.4.r.4.s)/2	(p) q (r) s (p³.4.q.4.r³.4.s.4)/2
(3/2 5/3 3 5/2)	(4.3/2.4.5/3.4.3.4.5/2)/2 gidrid U75^[en]	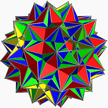(3/2³.4.5/3.4.3³.4.5/2.4)/2 gidisdrid Скиллинга^[en]

Примечания

Литература

Roman E. Maeder. Computer Science with Mathematica. — Cambridge University Press, 2000. — ISBN 0-521-63172-6,0-521-66395-4.
Дьяконов В. П. Mathematica 5.1/5.2/6. Программирование и математические вычисления. — М.: ДМК-Пресс, 2008. — ISBN 5-94074-405-2.
H. S. M. Coxeter. Regular Polytopes^[en]. — 3rd edition. — New York: Dover Publications Inc., 1973. — ISBN 0-486-61480-8.

Ссылки

Richard Klitzing: Polyhedra by

Zvi Har'El:

Uniform Solution for Uniform Polyhedra

Данная страница на сайте WikiSort.ru содержит текст со страницы сайта "Википедия".

Если Вы хотите её отредактировать, то можете сделать это на странице редактирования в Википедии.

Если сделанные Вами правки не будут кем-нибудь удалены, то через несколько дней они появятся на сайте WikiSort.ru .

Текст в блоке "Читать" взят с сайта "Википедия" и доступен по лицензии Creative Commons Attribution-ShareAlike; в отдельных случаях могут действовать дополнительные условия.

Другой контент может иметь иную лицензию. Перед использованием материалов сайта WikiSort.ru внимательно изучите правила лицензирования конкретных элементов наполнения сайта.

2019-2025
WikiSort.ru - проект по пересортировке и дополнению контента Википедии

[_f8c487fd0e258337-1] Maeder, 2000.

[_462ca2c0a95b9ac9-2] Дьяконов, 2008.

[_4c510b24a26a2a17-3] Coxeter, 1973.

[4] Guy Inchbald – Trimethoric (and trisynaptic) polyhedra

3/2.4.3.4 thah U4 hemi(3 3/2 \| 2)	4/3.6.4.6 cho U15^[en] hemi(4 4/3 \| 3)	5/4.10.5.10 sidhid U51^[en] hemi(5 5/4 \| 5)	5/2.6.5/3.6 sidhei U62^[en] hemi(5/2 5/3 \| 3)	5/2.10/3.5/3.10/3 gidhid U70^[en] hemi(5/2 5/3 \| 5/3)
	3/2.6.3.6 oho U3^[en] hemi(?)	3/2.10.3.10 seihid U49^[en] hemi(3 3/2 \| 5)	5.6.5/4.6 gidhei U65^[en] hemi(5 5/4 \| 3)	3.10/3.3/2.10/3 geihid U71^[en] hemi(3 3/2 \| 5/3)