WikiSort.ru - Не сортированное

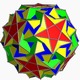
Статья содержит список однородных и звёздчатых многогранников из книги Модели многогранников Магнуса Веннинджера.

Книга написана как руководство по построению физических моделей многогранников. Книга включает чертежи элементов граней для построения, рекомендации, полезные для построения, а также короткое описание теории, связанной с этими фигурами. Книга содержит 75 непризматических однородных многогранников^[en] и 44 звёздчатых форм выпуклых правильных и полуправильных многогранников.

Этот список создан как дань уважения ранней работе Веннинджера и чтобы дать детальные ссылки на 119 пронумерованных моделей книги.

На модели, перечисленные здесь, можно ссылаться как на «Модель Веннинджера Номер N» или, для краткости, W_N.

Многогранники собраны в пять таблиц: правильные (1–5), полуправильные (6–18), правильные звёздчатые многогранники (20–22, 41), звёздчатые формы и соединения (19–66) и однородные звёздчатые многогранники (67–119). Четыре правильных звёздчатых многогранника приведены дважды, поскольку они принадлежат как однородным многогранникам, так и звёздчатым формам.

Правильные многогранники (плато́новы тела) W1 to W5

Номер	Название	Рисунок	Имя двойственного	Рисунок двойственного	Символ Витхоффа[en]	Вершинная фигура и символ Шлефли	Группа симметрии	U#	K#	V	E	F	Грани по типам
1	Тетраэдр		Тетраэдр		3|2 3	{3,3}	Td	U01	K06	4	6	4	4{3}
2	Октаэдр		Гексаэдр		4|2 3	{3,4}	Oh	U05	K10	6	12	8	8{3}
3	Гексаэдр (Куб)		Октаэдр		3|2 4	{4,3}	Oh	U06	K11	8	12	6	6{4}
4	Икосаэдр		Додекаэдр		5|2 3	{3,5}	Ih	U22	K27	12	30	20	20{3}
5	Додекаэдр		Икосаэдр		3|2 5	{5,3}	Ih	U23	K28	20	30	12	12{5}

Архимедовы тела (Полуправильные) W6 to W18

Номер	Название	Рисунок	Имя двойственного	Рисунок двойственного	Символ Витхоффа[en]	Вершинная фигура и символ Шлефли	Группа симметрии	U#	K#	V	E	F	Грани по типам
6	Усечённый тетраэдр		триакистетраэдр		2 3|3	3.6.6	Td	U02	K07	12	18	8	4{3} + 4{6}
7	Усечённый октаэдр		тетракисгексаэдр		2 4|3	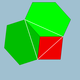4.6.6	Oh	U08	K13	24	36	14	6{4} + 8{6}
8	Усечённый гексаэдр		триакисоктаэдр		2 3|4	3.8.8	Oh	U09	K14	24	36	14	8{3} + 6{8}
9	Усечённый икосаэдр		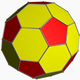пентакисдодекаэдр		2 5|3	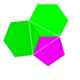5.6.6	Ih	U25	K30	60	90	32	12{5} + 20{6}
10	Усечённый додекаэдр		триакисикосаэдр		2 3|5	3.10.10	Ih	U26	K31	60	90	32	20{3} + 12{10}
11	Кубооктаэдр		ромбододекаэдр		2|3 4	3.4.3.4	Oh	U07	K12	12	24	14	8{3} + 6{4}
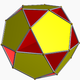
12	Икосододекаэдр		ромботриаконтаэдр		2|3 5	3.5.3.5	Ih	U24	K29	30	60	32	20{3} + 12{5}
13	Ромбокубооктаэдр		дельтоидальный икоситетраэдр		3 4|2	3.4.4.4	Oh	U10	K15	24	48	26	8{3}+(6+12){4}
14	Ромбоикосидодекаэдр		дельтоидальный гексеконтаэдр		3 5|2	3.4.5.4	Ih	U27	K32	60	120	62	20{3} + 30{4} + 12{5}
15	Усечённый кубооктаэдр (Большой ромбокубооктаэдр)		ромбоусечённый додекаэдр[en]		2 3 4|	4.6.8	Oh	U11	K16	48	72	26	12{4} + 8{6} + 6{8}
16	Ромбоусечённый икосододекаэдр (Большой ромбоикосододекаэдр)		Гекзакисикосаэдр		2 3 5|	4.6.10	Ih	U28	K33	120	180	62	30{4} + 20{6} + 12{10}
17	Плосконосый куб		пятиугольный икосотетраэдр[en]		|2 3 4	3.3.3.3.4	O	U12	K17	24	60	38	(8 + 24){3} + 6{4}
18	Плосконосый додекаэдр		пятиугольный гексаконтаэдр[en]		|2 3 5	3.3.3.3.5	I	U29	K34	60	150	92	(20 + 60){3} + 12{5}

Тела Кеплера — Пуансо (Правильные звёздчатые многогранники) W20, W21, W22 и W41

Номер	Название	Рисунок	Имя двойственного	Рисунок двойственного	Символ Витхоффа[en]	Вершинная фигура и символ Шлефли	Группа симметрии	U#	K#	V	E	F	Грани по типам
20	Малый звёздчатый додекаэдр		Большой додекаэдр		5|25/2	{5/2,5}	Ih	U34	K39	12	30	12	12{5/2}
21	Большой додекаэдр		Малый звёздчатый додекаэдр		5/2|2 5	{5,5/2}	Ih	U35	K40	12	30	12	12{5}
22	Большой звёздчатый додекаэдр		Большой икосаэдр		3|25/2	{5/2,3}	Ih	U52	K57	20	30	12	12{5/2}
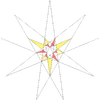
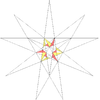
41	Большой икосаэдр (16-ая звёздчатая форма икосаэдра)		Большой звёздчатый додекаэдр		5/2|2 3	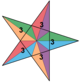{3,5/2}	Ih	U53	K58	12	30	20	20{3}

Звёздчатые многогранники: модели от W19 до W66

Звёздчатый октаэдр

Номер	Название	Группа симметрии	Рисунок	Грани
2	Октаэдр (правильный)	Oh
19	Звёздчатый октаэдр (Соединение двух тетраэдров)	Oh

Звёздчатые формы додекаэдра

Номер	Название	Группа симметрии	Рисунок	Грани
5	Додекаэдр (правильный)	Ih
20	Малый звёздчатый додекаэдр(правильный) (Первая звёздчатая форма додекаэдра)	Ih
21	Большой додекаэдр (правильный) (Вторая звёздчатая форма додекаэдра)	Ih
22	Большой звёздчатый додекаэдр(правильный) (Третья звёздчатая форма додекаэдра)	Ih

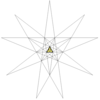
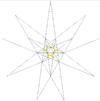
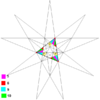
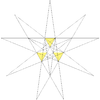
Звёздчатые формы икосаэдра

Номер	Название	Группа симметрии	Рисунок	Грани
4	Икосаэдр (правильный)	Ih
23	Соединение пяти октаэдров (Первая составная форма звёздчатого икосаэдра)	Ih
24	Соединение пяти тетраэдров (Вторая составная форма звёздчатого икосаэдра)	I
25	Соединение десяти тетраэдров[en] (Третья составная форма звёздчатого икосаэдра)	Ih
26	Малый триамбический икосаэдр (Первая звёздчатая форма икосаэдра) (Триакисикосаэдр)	Ih
27	Вторая звёздчатая форма икосаэдра	Ih
28	Выемчатый додекаэдр[en] (Третья звёздчатая форма икосаэдра)	Ih
29	Четвёртая звёздчатая форма икосаэдра[en]	Ih
30	Пятая звёздчатая форма икосаэдра[en]	Ih
31	Шестая звёздчатая форма икосаэдра[en]	Ih
32	Седьмая звёздчатая форма икосаэдра[en]	Ih
33	Восьмая звёздчатая форма икосаэдра[en]	Ih
34	Девятая звёздчатая форма икосаэдра[en] Большой триамбикикосаэдр[en]	Ih
35	Десятая звёздчатая форма икосаэдра[en]	I
36	Одиннадцатая звёздчатая форма икосаэдра[en]	I
37	Двенадцатая звёздчатая форма икосаэдра[en]	Ih
38	Тринадцатая звёздчатая форма икосаэдра[en]	I
39	Четырнадцатая звёздчатая форма икосаэдра[en]	I
40	Пятнадцатая звёздчатая форма икосаэдра[en]	I
41	Большой икосаэдр (правильный) (Шестнадцатая звёздчатая форма икосаэдра)	Ih
42	Ехиднаэдр (Завершающая, семнадцатая звёздчатая форма икосаэдра)	Ih

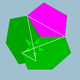
Звёздчатые формы кубооктаэдра

Номер	Название	Группа симметрии	Рисунок	Грани (октаэдральные плоскости)	Грани (кубические плоскости)
11	Кубооктаэдр (правильный)	Oh
43	Соединение куба и октаэдра[en] (Первая звёздчатая форма кубооктаэдра)	Oh
44	Вторая звёздчатая форма кубооктаэдра	Oh
45	Третья звёздчатая форма кубооктаэдра	Oh
46	Четвёртая звёздчатая форма кубооктаэдра	Oh

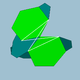
Звёздчатые формы икосододекаэдра

Номер	Название	Группа симметрии	Рисунок	Грани (икосоэдральные плоскости)	Грани (додекаэдральные плоскости)
12	Икосододекаэдр (правильный)	Ih
47	(Первая звёздчатая форма икосододекаэдра) Соединение додекаэдра и икосаэдра[en]	Ih
48	Вторая звёздчатая форма икосододекаэдра	Ih
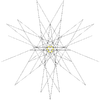49	Третья звёздчатая форма икосододекаэдра	Ih
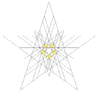50	Четвёртая звёздчатая форма икосододекаэдра (Соединение малого звёздчатого додекаэдра и триакисикосаэдра)	Ih
51	Пятая звёздчатая форма икосододекаэдра ( Соединение малого звёздчатого додекаэдра и пяти октаэдров)	Ih
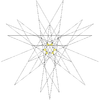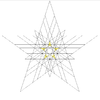52	Шестая звёздчатая форма икосододекаэдра	Ih
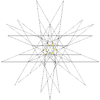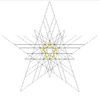53	Седьмая звёздчатая форма икосододекаэдра	Ih
54	Восьмая звёздчатая форма икосододекаэдра (Соединение пяти тетраэдров и большого додекаэдра)	I
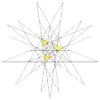55	Девятая звёздчатая форма икосододекаэдра	Ih
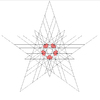56	Десятая звёздчатая форма икосододекаэдра	Ih
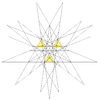57	Одиннадцатая звёздчатая форма икосододекаэдра	Ih
58	Двенадцатая звёздчатая форма икосододекаэдра	Ih
59	Тринадцатая звёздчатая форма икосододекаэдра	Ih
60	Четырнадцатая звёздчатая форма икосододекаэдра	Ih
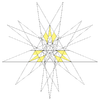61	Соединение большого звёздчатого додекаэдра и большого икосаэдра[en]	Ih
62	Пятнадцатая звёздчатая форма икосододекаэдра	Ih
63	Шестнадцатая звёздчатая форма икосододекаэдра	Ih
64	Семнадцатая звёздчатая форма икосододекаэдра	Ih
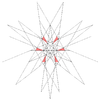65	Восемнадцатая звёздчатая форма икосододекаэдра	Ih
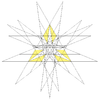66	Девятнадцатая звёздчатая форма икосододекаэдра	Ih

Однородные невыпуклые тела W67 - W119

Номер	Название	Рисунок	Название двойственного	Рисунок двойственного	Символ Витхоффа[en]	Вершинная фигура	Группа симметрии	U#	K#	V	E	F	Грани по типам
67	Тетрагемигексаэдр		Тетрагемигексакрон[en]		3/23|2	4.3/2.4.3	Td	U04	K09	6	12	7	4{3}+3{4}
68	Октагемиоктаэдр[en]		Октагемиоктакрон[en]		3/23|3	6.3/2.6.3	Oh	U03	K08	12	24	12	8{3}+4{6}
69	Малый кубокбооктаэдр[en]		Малый гексакронный икосотетраэдр[en]		3/24|4	8.3/2.8.4	Oh	U13	K18	24	48	20	8{3}+6{4}+6{8}
70	Малый битригональный икосододекаэдр[en]		Малый триамбический икосаэдр		3|5/23	(5/2.3)3	Ih	U30	K35	20	60	32	20{3}+12{5/2}
71	Малый икосоикосододекаэдр[en]		Малый икосакронный гексаконтаэдр[en]		5/23|3	6.5/2.6.3	Ih	U31	K36	60	120	52	20{3}+12{5/2}+20{6}
72	Малый додекоикосододекаэдр[en]		Малый додекакронный гексаконтаэдр[en]		3/25|5	10.3/2.10.5	Ih	U33	K38	60	120	44	20{3}+12{5}+12{10}
73	Додекододекаэдр		Средний ромбический триаконтаэдр[en]		2|5/25	(5/2.5)2	Ih	U36	K41	30	60	24	12{5}+12{5/2}
74	Малый ромбододекаэдр[en]		Малый ромбододекакрон[en]		25/25|	10.4.10/9.4/3	Ih	U39	K44	60	120	42	30{4}+12{10}
75	Усечённый большой додекаэдр[en]		Малый звёздчатый пентакисдодекаэдр[en]		25/2|5	10.10.5/2	Ih	U37	K42	60	90	24	12{5/2}+12{10}
76	Ромбододекододекаэдр[en]		Средний дельтоидный гексаконтаэдр[en]		5/25|2	4.5/2.4.5	Ih	U38	K43	60	120	54	30{4}+12{5}+12{5/2}
77	Большой кубокубооктаэдр[en]		Большой гексакронный икосотетраэдр[en]		3 4|4/3	8/3.3.8/3.4	Oh	U14	K19	24	48	20	8{3}+6{4}+6{8/3}
78	Кубогемиоктаэдр[en]		Гексагемиоктакрон[en]		4/34|3	6.4/3.6.4	Oh	U15	K20	12	24	10	6{4}+4{6}
79	Кубоусечённый кубооктаэдр[en] (Кубооктаусечённый кубооктаэдр)		Тетрадиакисгексаэдр[en]		4/33 4|	8/3.6.8	Oh	U16	K21	48	72	20	8{6}+6{8}+6{8/3}
80	Битригональный додекаэдр[en]		Средний триамбикикосаэдр[en]		3|5/35	(5/3.5)3	Ih	U41	K46	20	60	24	12{5}+12{5/2
81	Большой битригональный додекоикосододекаэдр[en]		Большой битриагональный додекакронный гексаконтаэдр[en]		3 5|5/3	10/3.3.10/3.5	Ih	U42	K47	60	120	44	20{3}+12{5}+12{10/3}
82	Малый битригональный додекоикосододекаэдр[en]		Малый битриагональный додекакронный гексаконтаэдр[en]		5/33|5	10.5/3.10.3	Ih	U43	K48	60	120	44	20{3}+12{5/2}+12{10}
83	Иикосододекододекаэдр[en]		Средний икосакронный гексаконтаэдр[en]		5/35|3	6.5/3.6.5	Ih	U44	K49	60	120	44	12{5}+12{5/2}+20{6}
84	Икосоусечённый додекододекаэдр[en] (Икосододекоусечённый икосододекаэдр)		Тридиакисикосаэдр[en]		5/33 5|	10/3.6.10	Ih	U45	K50	120	180	44	20{6}+12{10}+12{10/3}
85	Невыпуклый большой ромбокубооктаэдр[en] (Квазиромбокубооктаэдр)		Большой дельтоидный икосотетраэдр[en]		3/24|2	4.3/2.4.4	Oh	U17	K22	24	48	26	8{3}+(6+12){4}
86	Малый ромбогексаэдр[en]		Малый ромбогексакрон[en]		3/22 4|	4.8.4/3.8	Oh	U18	K23	24	48	18	12{4}+6{8}
87	Большой битигональный икосододекаэдр[en]		Большой триамбикикосаэдр[en]		3/2|3 5	(5.3.5.3.5.3)/2	Ih	U47	K52	20	60	32	20{3}+12{5}
88	Большой икосоикосододекаэдр[en]		Большой икосакронный гексаконтаэдр[en]		3/25|3	6.3/2.6.5	Ih	U48	K53	60	120	52	20{3}+12{5}+20{6}
89	Малый икосогемидодекаэдр[en]		Малый икосогемидодекакрон[en]		3/23|5	10.3/2.10.3	Ih	U49	K54	30	60	26	20{3}+6{10}
90	Малый додекоикосаэдр[en]		Малый додекоикосакрон[en]		3/23 5|	10.6.10/9.6/5	Ih	U50	K55	60	120	32	20{6}+12{10}
91	Малый додекогемидодекаэдр[en]		Малый додекогемидодекакрон[en]		5/45|5	10.5/4.10.5	Ih	U51	K56	30	60	18	12{5}+6{10}
92	Звёздчатый усечённый гексаэдр[en] (Квазиусечённый гексаэдр)		Большой триакисоктаэдр[en]		2 3|4/3	8/3.8/3.3	Oh	U19	K24	24	36	14	8{3}+6{8/3}
93	Большой усечённый кубооктаэдр[en] (Квазиусечённый кубооктаэдр)		Большой дисдиакисдодекаэдр[en]		4/32 3|	8/3.4.6	Oh	U20	K25	48	72	26	12{4}+8{6}+6{8/3}
94	Большой икосододекаэдр[en]		Большой ромботриаконтаэдр[en]		2|5/23	(5/2.3)2	Ih	U54	K59	30	60	32	20{3}+12{5/2}
95	Усечённый большой икосаэдр[en]		Большой звёздчатый пентакисдодекаэдр[en]		25/2|3	6.6.5/2	Ih	U55	K60	60	90	32	12{5/2}+20{6}
96	Ромбоикосаэдр[en]		Ромбоикоакрон[en]		25/23|	6.4.6/5.4/3	Ih	U56	K61	60	120	50	30{4}+20{6}
97	Малый звёздчатый усечённый додекаэдр[en] (Квазиусечённый звёздчатый додекаэдр)		Большой пентакисдодекаэдр[en]		2 5|5/3	10/3.10/3.5	Ih	U58	K63	60	90	24	12{5}+12{10/3}
98	Усечённый додекадодекаэдр[en] (Квазиусечённый додекаэдр)		Средний дисдиакистриаконтаэдр[en]		5/32 5|	10/3.4.10	Ih	U59	K64	120	180	54	30{4}+12{10}+12{10/3}
99	Большой додекоикосододекаэдр[en]		Большой додекакроникгексаконтаэдр[en]		5/23|5/3	10/3.5/2.10/3.3	Ih	U61	K66	60	120	44	20{3}+12{5/2}+12{10/3 }
100	Малый додекогемиикосаэдр[en]		Малый додекогемиикосакрон[en]		5/35/2|3	6.5/3.6.5/2	Ih	U62	K67	30	60	22	12{5/2}+10{6}
101	Большой додекоикосаэдр[en]		Большой додекоикосакрон[en]		5/35/23|	6.10/3.6/5.10/7	Ih	U63	K68	60	120	32	20{6}+12{10/3}
102	Большой додекогемиикосаэдр[en]		Большой додекогемиикосакрон[en]		5/45|3	6.5/4.6.5	Ih	U65	K70	30	60	22	12{5}+10{6}
103	Большой ромбогексаэдр		Большой ромбогексакрон		4/33/22|	4.8/3.4/3.8/5	Oh	U21	K26	24	48	18	12{4}+6{8/3}
104	Большой звёздчатый усечённый додекаэдр[en] (Квазиусечённый большой звёздчатый додекаэдр)		Большой триакисикосаэдр[en]		2 3|5/3	10/3.10/3.3	Ih	U66	K71	60	90	32	20{3}+12{10/3}
105	Невыпуклый большой ромбоикосододекаэдр[en] (Квазиромбоикосододекаэдр)		Большой дельтоидальный гексаконтаэдр[en]		5/33|2	4.5/3.4.3	Ih	U67	K72	60	120	62	20{3}+30{4}+12{5/2}
106	Большой икосогемидодекаэдр[en]		Большой икосогемидодекакрон[en]		3 3|5/3	10/3.3/2.10/3.3	Ih	U71	K76	30	60	26	20{3}+6{10/3}
107	Большой додекогемидодекаэдр[en]		Большой додекогемидодекакрон[en]		5/35/2|5/3	10/3.5/3.10/3.5/2	Ih	U70	K75	30	60	18	12{5/2}+6{10/3}
108	Большой усечённый икосододекаэдр[en] (Большой квазиусечённый икосододекаэдр)		Большой дисдиакистриаконтаэдр[en]		5/32 3|	10/3.4.6	Ih	U68	K73	120	180	62	30{4}+20{6}+12{10/3}
109	Большой ромбододекаэдр[en]		Большой ромбододекакрон[en]		3/25/32|	4.10/3.4/3.10/7	Ih	U73	K78	60	120	42	30{4}+12{10/3}
110	Малый плосконосый икосоикосододекаэдр[en]		Малый шестиугольный гексаконтаэдр[en]		|5/23 3	3.3.3.3.3.5/2	Ih	U32	K37	60	180	112	(40+60){3}+12{5/2}
111	Плосконосый додекододекаэдр[en]		Средний пятиугольный гексаконтаэдр[en]		|25/25	3.3.5/2.3.5	I	U40	K45	60	150	84	60{3}+12{5}+12{5/2}
112	Плосконосый икосододекододекаэдр[en]		Средний шестиугольный гексаконтаэдр[en]		|5/33 5	3.3.3.3.5.5/3	I	U46	K51	60	180	104	(20+6){3}+12{5}+12{5/2}
113	Большой вывернутый плосконосый икосододекаэдр[en]		Большой вывернутый пятиугольный гексаконтаэдр[en]		|5/32 3	3.3.3.3.5/3	I	U69	K74	60	150	92	(20+60){3}+12{5/2}
114	Вывернутый плосконосый додекододекаэдр[en]		Малый вывернутый пятиугольный гексаконтаэдр[en]		|5/32 5	3.5/3.3.3.5	I	U60	K65	60	150	84	60{3}+12{5}+12{5/2}
115	Большой плосконосый додекоикосододекаэдр[en]		Большой шестиугольный гексаконтаэдр[en]		|5/35/23	3.5/3.3.5/2.3.3	I	U64	K69	60	180	104	(20+60){3}+(12+12){5/2}
116	Большой плосконосый икосододекаэдр[en]		Большой пятиугольный гексаконтаэдр[en]		|25/25/2	3.3.3.3.5/2	I	U57	K62	60	150	92	(20+60){3}+12{5/2}
117	Большой вывернутый обратноплосконосый икосододекаэдр		Большой пентаграммный гексаконтаэдр[en]		|3/25/32	(3.3.3.3.5/2)/2	I	U74	K79	60	150	92	(20+60){3}+12{5/2}
118	Малый вывернутый обратноплосконосый икосоикосододекаэдр[en]		Малый гексаграммный гексаконтаэдр[en]		|3/23/25/2	(3.3.3.3.3.5/2)/2	Ih	U72	K77	180	60	112	(40+60){3}+12{5/2}
119	Большой биромбоикосододекаэдр[en]		Большой биромбоикосододекрон[en]		|3/25/335/2	(4.5/3.4.3.4.5/2.4.3/2)/2	Ih	U75	K80	60	240	124	40{3}+60{4}+24{5/2}

См. также

• Список однородных многогранников
• Список пятидесяти девяти икосаэдров

Литература

• М. Веннинджер. Модели многогранников. — «Мир», 1974. Ошибки: В книге Веннинджера вершинная фигура для многогранника W90 ошибочно показана как имеющая параллельные рёбра.
• Magnus Wenninger. Spherical Models. — Cambridge University Press, 1979. — ISBN 0-521-29432-0.

Ссылки

• Magnus J. Wenninger
• Software used to generate images in this article:
  • Stella: Polyhedron Navigator Stella (software) - Can create and print nets for all of Wenninger's polyhedron models.
  • Vladimir Bulatov's Polyhedra Stellations Applet
  • Vladimir Bulatov's Polyhedra Stellations Applet packaged as an OS X application
• M. Wenninger, Polyhedron Models, Errata: known errors in the various editions.

Для улучшения этой статьи желательно: Проверить качество перевода с иностранного языка. Исправить статью согласно стилистическим правилам Википедии.