WikiSort.ru - Не сортированное

Усечённый квадрат является правильным восьмиугольником: t{4} = {8} =

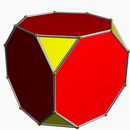Усечённый куб t{4,3} или

Усечённые кубические соты[en] t{4,3,4} или

В геометрии усечение — это операция в пространстве любой размерности, которая отсекает вершины политопа и при которой образуются новые грани на месте вершин. Термин берёт начало от названий архимедовых тел, данных Кеплером.

Однородное отсечение

В общем случае любой многогранник может быть усечён с некоторой степенью свободы выбора глубины усечения, что показано в статье Нотация Коксетера^[en].

Обычно применяемый вид усечения — однородное усечение, при котором операция усечения применяется к правильному многограннику и результатом которого получается однородный многогранник^[en] с равными длинами рёбер. В этом случае нет свободы выбора и в результате получаем вполне определённые геометрические тела, похожие на правильные многогранники.

В общем случае все однородные многогранники с одним обведённым узлом (в диаграмме Коксетера — Дынкина) имеют однородное усечение. Например, икосододекаэдр, предствленный символами Шлефли r{5,3} или ${\displaystyle {\begin{Bmatrix}5\\3\end{Bmatrix}}}$ и имеющий диаграммы Коксетера — Дынкина или , имеет однородное усечение — ромбоусечённый икосододекаэдр с нотациями tr{5,3} или ${\displaystyle t{\begin{Bmatrix}5\\3\end{Bmatrix}}}$ , . В диаграмме Коксетера — Дынкина эффект усечения проявляется в том, что у всех узлов, смежных с обведённым, появляются кружки.

Усечение многоугольников

Усечённый n-сторонний многоугольник будет иметь 2n сторон. Однородно усечённый правильный многоугольник становится другим правильным многоугольником: t{n} = {2n}. Полное усечение, r{3}, является другим правильным многоугольником, двойственным^[en] исходному.

Правильные многоугольники можно также представить диаграммой Коксетера — Дынкина, , и его однородное усечение будет иметь диаграмму , а его полное усечение — диаграмму . Граф представляет группу Коксетера I₂(n), в которой каждый узел является зеркалом, а каждое ребро представляет угол π/n между зеркалами, кружки же вокруг одного или двух зеркал показывают, какие из них активны.

Параметрическое усечение треугольника

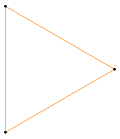{3}

t{3} = {6}

r{3} = {3}

Звёздчатые многоугольники могут быть тоже усечены. Усечённая пентаграмма {5/2} будет выглядеть как пятиугольник, но, в действительности, является дважды накрытым (вырожденным) десятиугольником ({10/2}) с двумя множествами наложенных друг на друга вершин и сторон. Усечённая большая гептаграмма (семиугольная звезда) {7/3} даёт четырнадцатиугольную звезду {14/3}.

Однородное усечение правильных многогранников и мозаик

Когда речь идёт об усечении правильных многогранников или мозаик из правильных многоугольников^[en], обычно использыется «однородное усечение», что предполагает усечение до состояния, когда исходные грани становятся правильными многоугольниками с удвоенным числом сторон.

Последовательность на рисунке показывает пример усечения куба, где показаны четыре шага из непрерывного процесса усечения от полного куба до полного усечения куба. Конечное тело — кубооктаэдр.

Среднее изображение является однородным усечённым кубом. Он представлен символом Шлефли t{p,q,…}.

Глубокое усечение^[en] — это более сильное усечение, удаляющее все исходные рёбра, но оставляющие внутренние части исходных граней. Например, усечённый октаэдр является глубоко усечённым кубом: 2t{4,3}.

Полное глубокое усечение называется биректификацией и оно сводит исходные грани к точкам. Многогранник при этом превращается в двойственный многогранник. Например, октаэдр является полным глубоким усечением куба: {3,4} = 2r{4,3}.

Ещё один тип усечения — всестороннее усечение^[en], при котором отсекаются рёбра и вершины, что даёт прямоугольники вместо рёбер.

Многогранники в более высоких размерностях имеют другие уровни усечений — ранцинацию^[en], при которой отсекаются грани, рёбра и вершины. В размерностях выше 5 существует стерикация^[en], при которой отсекаются грани, рёбра и вершины, а также трёхмерные грани.

Усечение рёбер

Усечение рёбер — это снятие фаски с многогранника, как в случае всестороннего усечения, но вершины при этом остаются, а рёбра заменяются шестиугольниками. В 4-мерном многограннике рёбра заменяются на удлинённые бипирамиды^[en].

Альтернации или частичные усечения

Альтернация или частичное усечение удаляет только некоторые из исходных вершин.

При частичном усечении или альтернации^[en] половина вершин и рёбер полностью удаляется. Операция применима к многогранникам, грани которого имеют чётное число сторон. Грани сокращают число сторон вдвое, а квадратные грани переходят рёбра. Например, тетраэдр является альтернацией куба, h{4,3}.

Умаление^[en] — более общий термин, использующийся для многогранников Джонсона, предполагает удаление одной или более вершин, рёбер или граней не трогая оставшиеся вершины. Например, триуменьшенный икосаэдр^[en] получается из правильного икосаэдра путём удаления трёх вершин.

Другие частичные усечения основываются на симметрии. Например, тетраэдрально уменьшенный додекаэдр^[en].

Обобщённые усечения

Процесс линейного усечения может быть обобщён путём разрешения параметра усечения быть отрицательным или разрешения проходить через середину ребра, что даёт самопересекающиеся звёздчатые многогранники. Такие многогранники могут быть связаны с некоторыми правильными звёздчатыми многоугольниками^[en] и однородными звёздчатыми многогранниками.

• Мелкое усечение — рёбра уменьшаются в размерах, грани удваивают число сторон, на месте бывших вершин образуются новые грани.
• Однородное усечение — специальный случай, при котором все полученные рёбра имеют одинаковую длину. В усечённом кубе, t{4,3}, квадратные грани превращаются в восьмиугольники, а вместо вершин образуются треугольники.
• Антиусечение обратно мелкому усечению. В результате получается многогранник, который похож на исходный, но имеет части, висящие на углах, вместо отрезания углов.
• Полное усечение — предельное мелкое усечение, где рёбра сводятся к точкам. Примером служит Кубооктаэдр, r{4,3}.
• Гиперусечение является видом усечения, которое идёт далее полного усечения, обращая исходные рёбра, что приводит к самопересечениям.
• Квазиусечение является видом усечения, идущего далее гиперусечения, где обращённые рёбра становятся длиннее исходных. Это усечение можно получить из исходного многогранника путём отступления граней от рёбер, то есть движению в обратную сторону от вершины. Например, квазиусечение квадрата даёт правильную октаграмму (t{4,3}={8/3}), а квазиусечение куба даёт однородный звёздчатый усечённый гексаэдр^[en], t{4/3,3}.

Усечения квадрата

Типы усечения квадрата, {4}. Исходные рёбра показаны красным цветом, а новые рёбра, полученные в результате усечения — голубым. Однородное усечение является правильным восьмиугольником, t{4}={8}. Полное усечение квадрата становится опять квадратом с диагональной ориентацией сторон. Вершины пронумерованы против часовой стрелки цифрами от 1 до 4, полученные в результате усечения пары отмечены буквами a и b.

Усечения куба

⇨	Куб {4,3}	⇨	Усечение t{4,3}	⇨	Полное усечение r{4,3}	⇩
Антиусечение						Гиперусечение
⇧	Полное квазиусечение	⇦	Квазиусечение t{4/3,3}[en]	⇦	Полное гиперусечение	⇦

См. также

• Однородный многогранник^[en]
• Однородный четырёхмерный многогранник^[en]
• Двойное усечение (геометрия)^[en]
• Полное усечение
• Альтернация (геометрия)^[en]
• Нотация многогранников Конвея^[en]

Примечания

Литература

• H. S. M Coxeter. Chapter 8: Truncation // Regular Polytopes^[en]. — 3rd edition. — New York: Dover Publications Inc, 1973. — С. 145–154. — ISBN 0-486-61480-8.
• Norman Johnson^[en]. Uniform Polytopes. — Manuscript, 1991.
• Norman Johnson^[en]. The Theory of Uniform Polytopes and Honeycombs. — University of Toronto: Ph.D. Dissertation, 1966.

Ссылки

• Weisstein, Eric W. Truncation (англ.) на сайте Wolfram MathWorld.
• Glossary ForH yperspace
• Polyhedra Names, truncation

Операции над многогранниками

Основа	Усечение	Полное усечение	Глубокое усечение[en]	Двойствен- ность	Растяжение	Всеусечение[en]	Альтернация[en]
t0{p, q} {p, q}	t01{p,q}[en] t{p, q}	t1{p,q} r{p, q}	t12{p,q}[en] 2t{p, q}	t2{p, q} 2r{p, q}	t02{p,q}[en] rr{p, q}	t012{p,q}[en] tr{p, q}	ht0{p,q}[en] h{q, p}	ht12{p,q} s{q, p}	ht012{p,q} sr{p, q}

Для улучшения этой статьи желательно: Проверить качество перевода с иностранного языка. Исправить статью согласно стилистическим правилам Википедии.