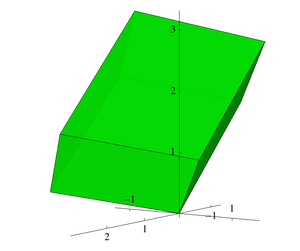
Дискриминант алгебраического числового поля — это числовой инвариант, который, грубо говоря, измеряет размер (кольца целых чисел[en]) алгебраического числового поля. Более конкретно, он пропорционален квадрату объёма фундаментальной области кольца целых чисел и он определяет, какие простые числа разветвляются[en].
Дискриминант является наиболее важным инвариантом числового поля и появляется в некоторых важных аналитических формулах, таких как функциональное уравнение[en] дзета-функции Дедекинда поля K и формула для числа классов[en] поля K. Старая теорема Эрмита утверждает, что имеется лишь конечное число числовых полей с ограниченным дискриминантом, однако определение этого числа остаётся открытой проблемой и является предметом исследований[1].
Дискриминант поля K может называться абсолютным дискриминантом поля K для того, чтобы отличить его от относительного дискриминанта расширения K/L числовых полей. Последнее является идеалом в кольце целых чисел поля L и подобно абсолютному дискриминанту показывает, какие простые числа разветвляются в K/L. Он является обобщением абсолютного дискриминанта, позволяющим полю L быть больше . Фактически, когда , относительный дискриминант является главным идеалом кольца , порождаемого абсолютным дискриминантом поля K.
Определение
Пусть K будет алгебраическим числовым полем и пусть OK будет его кольцом целых чисел[en]. Пусть будет целочисленным базисом[en] кольца OK (т.е. базис как Z-модуль), и пусть — множество вложений поля K в комплексные числа (т.е. инъективные гомоморфизмы колец ). Дискриминант поля K равен квадрату определителя n х n матрицы B, (i,j)-элементы которой равны . В символической форме,
Эквивалентно, можно использовать след из K в
. В частности, определим форму следа как матрицу, (i,j)-элементы которой равны
. Эта матрица равна BTB, так что дискриминант поля K является определителем этой матрицы.
Примеры
- Квадратичные числовые поля: пусть d является свободным от квадратов числом, тогда дискриминант поля равен[2]
- Целое число, которое появляется как дискриминант квадратичного числового поля, называется фундаментальным дискриминантом[3].
- Круговые поля: пусть n > 2 является целым числом, — примитивным n-ым корнем из единицы, а — n-ым круговым полем. Дискриминант поля задаётся формулой[2][4]
- где — функция Эйлера, а произведение в знаменателе пробегает по всем простым p, делящим n.
- Степенные базисы: В случае, когда кольцо целых чисел имеет степенной целочисленный базис[en], то есть может быть записано как , дискриминант поля K равен дискриминанту минимального многочлена от . Чтобы это увидеть, можно выбрать целочисленный базис кольца равным . Тогда матрица в определении является матрицей Вандермонда, ассоциированной с , квадрат определителя которого равен
- что в точности совпадает с определением дискриминанта минимального многочлена.
- Пусть будет числовым полем, полученным присоединением корня многочлена . Данный пример является оригинальным примером Дедекинда числового поля, кольцо целых чисел которого не обладает степенным базисом. Целочисленный базис задаётся как , а дискриминант поля K равен −503[5][6].
- Дублирующиеся дискриминанты: дискриминант квадратичного поля единственным образом определяет его, но в общем случае для числовых полей более высокой степени это неверно. Например, имеется два неизоморфных кубических поля[en] с дискриминантом 3969. Они получаются присоединением корня многочлена x3 − 21x + 28 или x3 − 21x − 35 соответственно[7].
Основные результаты
- Теорема Брилля[8]: Знак дискриминанта равен , где r2 — число комплексных точек поля K[9].
- Простое число p разветвляется в K тогда и только тогда, когда p делит [10].
- Теорема Штикельбергера[11]:
- или
- Граница Минковского[en][12]: Пусть n обозначает степень[en] расширения , а r2 обозначает число комплексных мест поля K, тогда
- Теорема Минковского[13]: Если K не равно , тогда (это следует прямо из границы Минковского).
- Теорема Эрмита — Минковского[en][14]: Пусть N — положительное целое. Существует лишь конечное число (с точностью до изоморфизма) алгебраических числовых полей K с . Снова, это следует из границы Минковского вместе с теоремой Эрмита (что существует лишь конечное число алгебраических полей с предписанным дискриминантом).
История

Определение дискриминанта общего алгебраического числового поля K было дано Дедекиндом в 1871[15]. В это время он уже знал о связи между дискриминантом и разветвлением[16].
Теорема Эрмита предшествовала общему определению дискриминанта и доказательство её Шарль Эрмит опубликовал в 1857[17]. В 1877 Александр фон Брилль определил знак детерминанта[18]. Леопольд Кронекер сформулировал теорему Минковского в 1882[19], хотя доказательство её Герман Минковский дал лишь в 1891[20]. В том же году Минковский опубликовал свою границу детерминанта[21]. К концу девятнадцатого века Штикельбергер, Людвиг[en] получил теорему об остатке дискриминанта по модулю четыре[22][23].
Относительный дискриминант
О дискриминанте, определённом выше, иногда говорят как об абсолютном дискриминанте поля K, чтобы отличить его от относительного дискриминанта расширения числовых полей K/L, который является идеалом в OL. Относительный дискриминант определяется так же, как и абсолютный дискриминант, но следует принимать во внимание, что идеал в OL может не быть главным и что OL может не быть базисом OK. Пусть будет множеством вложений K в , которые являются единицами на L. Если является каким-либо базисом поля K над L, пусть ) будет квадратом детерминанта n х n матрицы, (i,j)-элементы которой равны . Тогда относительный дискриминант расширения K/L является идеалом, порождённым , где пробегает по всем целочисленным базисам расширения K/L. (т.е. по базисам со свойством, что для всех i.) Альтернативно, относительный дискриминант расширения K/L равен норме[en] дифферента[en] K/L[24]. Когда , относительный дискриминант является главным идеалом кольца , порождаемым абсолютным дискриминантом . В башне полей K/L/F относительные дискриминанты связаны выражением
- ,
где обозначает относительную норму[25][26].
Разветвление
Относительный дискриминант определяет ветвление[en] расширения поля K/L. Главный идеал p поля L разветвляется в K тогда и только тогда, когда он делит относительный дискриминант . Расширение разветвляется тогда и только тогда, когда дискриминант является единичным идеалом[24]. Граница Минковского выше показывает, что не имеется нетривиальных неразветвлённых расширений поля . Поля, которые больше , могут иметь неразветвлённые расширения. Например, для любого поля с числом классов, бо́льшим единицы его гильбертово поле классов[en], является нетривиальным неразветвлённым расширением.
Корневой дискриминант
Корневой дискриминант числового поля K степени n, часто обозначаемый rdK, определяется как n-ый корень абсолютного значения (абсолютного) дискриминанта поля K[27]. Соотношения между относительными дискриминантами в башне полей показывает, что корневой дискриминант не меняется в неразветвлённом расширении. Существование башни полей классов даёт границы для корневого дискриминанта — существование бесконечной башни полей классов над , где m = 3·5·7·11·19, показывает, что имеется бесконечно иного полей с корневым дискриминантом 2√m ≈ 296,276[28]. Если r и 2s равны числу вещественных и комплексных вложений, так что , положим и . Обозначим через инфимум rdK для полей K с . Мы имеем (для достаточно больших)[28]
- ,
а в предположении верности обобщённой гипотезы Римана
Таким образом, мы имеем . Мартине показал, что и [28][29]. Войт[27] доказал, что для чисто вещественных полей корневой дискриминант > 14 с 1229 исключениями.
Связь с другими величинами
- При вложении в объём фундаментальной области кольца OK равен (иногда используется другая мера и объём получается равным , где r2 — число комплексных мест поля K).
- Поскольку дискриминант появляется в этой формуле для объёма, он также появляется в функциональном уравнении дзета-функция Дедекинда поля K, а потому также в аналитической формуле числа классов и в теореме Брауэра–Зигеля[en].
- Относительный дискриминант расширения K/L равен кондуктору Артина[en] регулярного представления[en] группы Галуа расширения K/L. Это даёт связь между кондукторами Артина и характерами[en] группы Галуа расширения K/L, которая называется формулой кондуктора-дискриминанта[en][30].
Примечания
- ↑ Cohen, Diaz y Diaz, Olivier, 2002.
- 1 2 Manin, Panchishkin, 2007, с. 130.
- ↑ Cohen, 1993, с. Definition 5.1.2.
- ↑ Washington, 1997, с. Proposition 2.7.
- ↑ Dedekind, 1878, с. 30–31.
- ↑ Narkiewicz, 2004, с. 64.
- ↑ Cohen, 1993, с. Theorem 6.4.6.
- ↑ Koch, 1997, с. 11.
- ↑ Washington, 1997, с. Lemma 2.2.
- ↑ Neukirch, 1999, с. Corollary III.2.12.
- ↑ Neukirch, 1999, с. Exercise I.2.7.
- ↑ Neukirch, 1999, с. Proposition III.2.14.
- ↑ Neukirch, 1999, с. Theorem III.2.17.
- ↑ Neukirch, 1999, с. Theorem III.2.16.
- 1 2 Приложение X Дедекинда во втором издании книги Дирихле Vorlesungen über Zahlentheorie (нем: Лекции по теории чисел) (Dedekind 1871)
- ↑ Bourbaki, 1994.
- ↑ Hermite, 1857.
- ↑ Brill, 1877.
- ↑ Kronecker, 1882.
- ↑ Minkowski, 1891a.
- ↑ Minkowski, 1891b.
- ↑ Stickelberger, 1897.
- ↑ Все факты этого параграфа можно найти в книге Наркиевича (Narkiewicz 2004, С. 59, 81)
- 1 2 Neukirch, 1999, с. §III.2.
- ↑ Neukirch, 1999, с. Corollary III.2.10.
- ↑ Fröhlich, Taylor, 1993, с. Proposition III.2.15.
- 1 2 Voight, 2008.
- 1 2 3 Koch, 1997, с. 181–182.
- ↑ Martinet, 1978, с. 65–73.
- ↑ Serre, 1967, с. Section 4.4.
Литература
- Yu. I.Manin, A. A. Panchishkin. Introduction to Modern Number Theory. — Second. — 2007. — Т. 49. — С. 130. — (Encyclopaedia of Mathematical Sciences). — ISBN 978-3-540-20364-3.
- Jacques Martinet. Tours de corps de classes et estimations de discriminants (фр.) // Inventiones Mathematicae. — 1978. — Т. 44. — DOI:10.1007/bf01389902. — .
- Alexander von Brill. Ueber die Discriminante // Mathematische Annalen. — 1877. — Т. 12, вып. 1. — С. 87–89. — DOI:10.1007/BF01442468.
- Richard Dedekind. Vorlesungen über Zahlentheorie von P.G. Lejeune Dirichlet. — 2. — Vieweg, 1871.
- Richard Dedekind. Über den Zusammenhang zwischen der Theorie der Ideale und der Theorie der höheren Congruenzen // Abhandlungen der Königlichen Gesellschaft der Wissenschaften zu Göttingen. — 1878. — Т. 23, вып. 1.
- Charles Hermite. Extrait d'une lettre de M. C. Hermite à M. Borchardt sur le nombre limité d'irrationalités auxquelles se réduisent les racines des équations à coefficients entiers complexes d'un degré et d'un discriminant donnés // Crelle's Journal. — 1857. — Т. 53. — С. 182–192. — DOI:10.1515/crll.1857.53.182.
- Leopold Kronecker. Grundzüge einer arithmetischen Theorie der algebraischen Grössen // Crelle's Journal. — 1882. — Т. 92. — С. 1–122.
- Hermann Minkowski. Ueber die positiven quadratischen Formen und über kettenbruchähnliche Algorithmen // Crelle's Journal. — 1891a. — Т. 107. — С. 278–297.
- Hermann Minkowski. Théorèmes d'arithmétiques // Comptes rendus de l'Académie des sciences. — 1891b. — Т. 112. — С. 209–212.
- Ludwig Stickelberger. Über eine neue Eigenschaft der Diskriminanten algebraischer Zahlkörper // Proceedings of the First International Congress of Mathematicians, Zürich. — 1897. — С. 182–193.
- Nicolas Bourbaki. Elements of the history of mathematics / Translated by Meldrum, John. — Berlin: Springer-Verlag, 1994. — ISBN 978-3-540-64767-6.
- Бурбаки Н. Очерки по истории математики. — М.: Издательство иностранной литературы, 1963.
- Henri Cohen. A Course in Computational Algebraic Number Theory. — Berlin, New York: Springer-Verlag, 1993. — Т. 138. — (Graduate Texts in Mathematics). — ISBN 978-3-540-55640-4.
- Henri Cohen, Francisco Diaz y Diaz, Michel Olivier. A Survey of Discriminant Counting // Algorithmic Number Theory, Proceedings, 5th International Syposium, ANTS-V, University of Sydney, July 2002 / Claus Fieker, David R. Kohel. — Berlin: Springer-Verlag, 2002. — Т. 2369. — С. 80–94. — (Lecture Notes in Computer Science). — ISBN 978-3-540-43863-2. — DOI:10.1007/3-540-45455-1_7.
- Albrecht Fröhlich, Martin J. Taylor. Algebraic number theory. — Cambridge University Press, 1993. — Т. 27. — (Cambridge Studies in Advanced Mathematics). — ISBN 978-0-521-43834-6.
- Helmut Koch. Algebraic Number Theory. — Springer-Verlag, 1997. — Т. 62. — (Encycl. Math. Sci.). — ISBN 3-540-63003-1.
- Władysław Narkiewicz. Elementary and analytic theory of algebraic numbers. — 3. — Berlin: Springer-Verlag, 2004. — (Springer Monographs in Mathematics). — ISBN 978-3-540-21902-6.
- Jürgen Neukirch. Algebraic Number Theory. — Berlin: Springer-Verlag, 1999. — Т. 322. — (Grundlehren der mathematischen Wissenschaften). — ISBN 978-3-540-65399-8.
- Jean-Pierre Serre. Local class field theory // Algebraic Number Theory, Proceedings of an instructional conference at the University of Sussex, Brighton, 1965 / J. W. S. Cassels, Albrecht Fröhlich. — London: Academic Press, 1967. — ISBN 0-12-163251-2.
- John Voight Voight. Enumeration of totally real number fields of bounded root discriminant // Algorithmic number theory. Proceedings, 8th International Symposium, ANTS-VIII, Banff, Canada, May 2008 / Alfred J. van der Poorten, Andreas Stein. — Berlin: Springer-Verlag, 2008. — Т. 5011. — С. 268–281. — (Lecture Notes in Computer Science). — ISBN 978-3-540-79455-4. — DOI:10.1007/978-3-540-79456-1_18.
- Lawrence Washington. Introduction to Cyclotomic Fields. — 2nd. — Berlin, New York: Springer-Verlag, 1997. — Т. 83. — (Graduate Texts in Mathematics). — ISBN 978-0-387-94762-4.
Литература для дальнейшего чтения
- James S. Milne. Algebraic Number Theory. — 1998.
Для улучшения этой статьи желательно: |
Данная страница на сайте WikiSort.ru содержит текст со страницы сайта "Википедия".
Если Вы хотите её отредактировать, то можете сделать это на странице редактирования в Википедии.
Если сделанные Вами правки не будут кем-нибудь удалены, то через несколько дней они появятся на сайте WikiSort.ru .



















![{\displaystyle O_{K}=\mathbb {Z} [\alpha ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0eb343eea81555e4a292e4127224d5ca6b56e033)






















![{\displaystyle \Delta _{K/F}={\mathcal {N}}_{L/F}\left({\Delta _{K/L}}\right)\Delta _{L/F}^{[K:L]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7f9f1950d56e6b263c691d3bb2178876560680aa)















