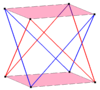
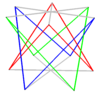
В геометрии пространственный многоугольник[1] — это многоугольник, вершины которого не компланарны. Пространственные многоугольники должны иметь по меньшей мере 4 вершины. Внутренняя поверхность таких многоугольников однозначно не определяется.
Пространственные бесконечноугольники[en] (апейрогоны) имеют вершины, не все из которых коллинеарны.
Зигзаг-многоугольник, или антипризматический многоугольник[2], имеет вершины, которые попеременно находятся на двух параллельных плоскостях, а потому, должны иметь чётное число сторон.
Правильный пространственный многоугольник в 3-мерном пространстве (и правильные пространственные бесконечноугольники[en] в 2-двумерном) всегда являются зигзаг-многоугольниками.
Антипризматические пространственные многоугольники в 3-мерном пространстве

Правильный пространственный многоугольник является изогональной фигурой с одинаковыми длинами сторон. В 3-мерном пространстве правильные пространственные многоугольники являются зигзаг-многоугольниками (антирпизматическими многоугольниками), вершины которых поочерёдно принадлежат двум параллельным плоскостям. Стороны n-антипризмы могут определять правильный пространственный 2n-угольник.
Правильному пространственному n-угольнику можно дать обозначение {p}#{ } как смесь обозначений правильного многоугольника {p} и ортогонального отрезка { }[3]. Симметрия между последовательными вершинами является скользящей.
Ниже в примерах показаны однородные квадратные и пятиугольные антипризмы. Звёздные антипризмы[en] также образуют правильные пространственные многоугольники с различным способом соединения вершин верхней и нижней звёзд.
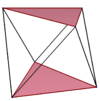
| Пространственный квадрат |
Пространственный шестиугольник |
Пространственный восьмиугольник |
| {2}#{ } | {3}#{ } | {4}#{ } |
 |
 |
 |
| sr{2,2} | sr{2,3} | sr{2,4} |
| Пространственный десятиугольник | ||
| {5}#{ } | {5/2}#{ } | {5/3}#{ } |
 |
 |
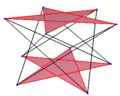 |
| sr{2,5} | sr{2,5/2}[en] | sr{2,5/3}[en] |
Правильный сложный пространственный 2n-угольник можно построить путём добавления второго пространственного 2n-угольника, полученного вращением первого. В этом случае вершины каждого из составляющих 2n-угольников лежат в вершинах призматической комбинации антипризм[en].
Многоугольники Петри — это правильные пространственные многоугольники, задаваемые внутри правильных многогранников и политопов. Например, 5 платоновых тел содержат 4, 6 и 10-сторонние правильные пространственные многоугольники, как видно из этих ортогональных проекций (красными отрезками показана проективная оболочка[en]). Тетраэдр и октаэдр включают все вершины в зигзаг-многоугольника и могут рассматриваться как антпризмы отрезков и треугольников соответственно.
Косой многоугольник[en] имеет правильные грани или вершинные фигуры в виде правильных пространственных многоугольников. Имеется бесконечно много заполняющих всё пространство правильных косых многоугольников[en] в 3-мерном пространстве и существуют косые многоугольники в 4-мерном пространстве, некоторые в виде однородного 4-мерного многогранника[en].
| {4,6|4} | {6,4|4} | {6,6|3} |
|---|---|---|
 Правильный косой шестиугольник {3}#{ } |
 Правильный косой квадрат {2}#{ } |
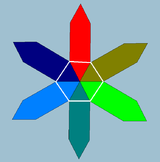 Правильный косой шестиугольник {3}#{ } |
Равноугольные пространственные многоугольники в 3-мерном пространстве
Изогогональный[en] пространственный многоугольник — это пространственный многоугольник с вершинами одного типа, соединёнными двумя типами сторон. Изогогональные пространственные многоугольники с равными длинами сторон можно считать полуправильными. Они подобны зигзаг-многоугольникам на двух плоскостях, за исключением того, что сторонам позволяется как переходить на другую плоскость, так и оставаться на той же плоскости.
Изогогональные пространственные многоугольники можно получить на n-угольных призмах с чётным числом сторон, попеременно двигаясь по сторонам многоугольника и межу многоугольниками. Например, по вершинам куба — проходим вершины вертикально по красным рёбрам и по синим рёбрам вдоль сторон квадратов оснований.
 Куб, квадрат-диагональ |
 Витая призма[en] |
 Куб |
 Пересечённый куб |
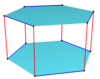 Шестигранная призма[en] |
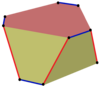 Шестигранная призма |
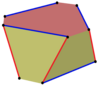 Шестигранная призма |
Правильные пространственные многоугольники в 4-мерном пространстве
В 4-мерном пространстве правильные пространственные многоугольники могут иметь вершины на торе Клиффорда и связаны смещением Клиффорда[en]. В отличие от зигзаг-многоугольников, пространственные многоугольники двойного вращения могут иметь нечётное число сторон.
Многоугольники Петри правильного 4-мерного многогранника определяют правильные пространственные многоугольники. Число Кокстера для каждой группы симметрий Коксетера выражает, сколько сторон имеет многоугольник Петри. Так, это будет 5-сторонний многоугольник для пятиячейника, 8-сторонний для тессеракта и шестнадцатиячейника, 12 сторон для двадцатичетырёхячейника и 30 сторон для стодвадцатиячейника и шестисотячейника.
Если ортогонально спроектировать эти правильные пространственные многоугольники на плоскость Коксетера[en], они превращаются в правильные огибающие многоугольники на плоскости.
| A4, [3,3,3] | B4, [4,3,3] | F4, [3,4,3] | H4, [5,3,3] | ||
|---|---|---|---|---|---|
| Пятиугольник, Пентаграмма | Восьмиугольник | Двенадцатиугольник | Тридцатиугольник[en] | ||
 пятиячейник {3,3,3} |
 тессеракт {4,3,3} |
 шестнадцатиячейник {3,3,4} |
 двадцатичетырёхячейник {3,4,3} |
 стодвадцатиячейник {5,3,3} |
 шестисотячейник {3,3,5} |
n-n дуопризма и двойственная дуопирамида[en] также имеют 2n-сторонние полигоны Петри. (тессеракт является 4-4 дуопризмой, а шестнадцатиячейник — 4-4 дуопирамидой.)
| Шестиугольник | Десятиугольник | Двенадцатиугольник | |||
|---|---|---|---|---|---|
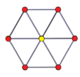 3-3 дуопризма |
 3-3 дуопризма |
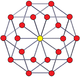 5-5 дуопризма[en] |
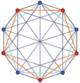 5-5 дуопризма[en] |
 6-6 дуопризма[en] |
 6-6 дуопризма[en] |
См. также
Примечания
- ↑ В английской литературе — skew polygon, буквально — косой многоугольник. В русской литературе прижился термин пространственный многоугольник, а термин косой многоугольник соответствует термину skew polyhedron (косой многогранник).
- ↑ Regular complex polytopes , p. 6
- ↑ Abstract Regular Polytopes, p.217
Литература
- Peter McMullen, Egon Schulte. Abstract Regular Polytopes // 1st. — Cambridge University Press, December 2002. — ISBN 0-521-81496-0.
- Robert Williams. Skew Polygons (Saddle Polygons). §2.2 // The Geometrical Foundation of Natural Structure: A Source Book of Design. — Dover Publications, Inc., 1979. — ISBN 0-486-23729-X.
- H. S. M.Coxeter. Chapter 1. Regular polygons, 1.5. Regular polygons in n dimensions, 1.7. Zigzag and antiprismatic polygons, 1.8. Helical polygons. 4.3. Flags and Orthoschemes, 11.3. Petrie polygons // Regular complex polytopes. — 1974.
- H. S. M.Coxeter. Разделы 2.6 Petrie Polygons с.24—25, Chapter 12, с.213—235, The generalized Petrie polygon // Regular Polytopes[en]. — 3rd ed. — New York: Dover, 1973.
- H. S. M. Coxeter, W. O. J. Moser. 5.2 The Petrie polygon {p,q}. // Generators and Relations for Discrete Groups. — New York: Springer-Verlag, 1980 (1st ed, 1957). — ISBN 0-387-09212-9.
- John Milnor. On the total curvature of knots // Ann. Math. — 1950. — Т. 52. — С. 248—257.
- J.M. Sullivan[en]. Curves of finite total curvature. — Technische Universität Berlin, 2006. — Июль. — arXiv:math.0606007v2.
Ссылки
- Weisstein, Eric W. Skew polygon (англ.) на сайте Wolfram MathWorld.
- Эрик В. Вайсштайн[en] Petrie polygon (недоступная ссылка) MathWorld
- Эрик В. Вайсштайн[en] Skew polygon (недоступная ссылка) MathWorld
Для улучшения этой статьи желательно: |
Данная страница на сайте WikiSort.ru содержит текст со страницы сайта "Википедия".
Если Вы хотите её отредактировать, то можете сделать это на странице редактирования в Википедии.
Если сделанные Вами правки не будут кем-нибудь удалены, то через несколько дней они появятся на сайте WikiSort.ru .