WikiSort.ru - Не сортированное

ПОИСК ПО САЙТУ | о проекте

Фигу́рные чи́сла — общее название чисел, связанных с той или иной геометрической фигурой. Это историческое понятие восходит к пифагорейцам. Предположительно, с понятием фигурного числа связано выражение «возвести число в квадрат или в куб».

Виды фигурных чисел

Со времён пифагорейцев традиционно различают следующие виды фигурных чисел (они определены, например, в VII книге «Начал» Евклида)^[1]:

Линейные числа — числа, не разлагающиеся на сомножители, то есть их ряд совпадает с рядом простых чисел, дополненным единицей (у Евклида используется термин «первые числа», πρώτοι αριθμοί):
1, 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97, 101, 103, 107, 109, 113, 127, 131, 137, 139, 149, 151, 157, 163, 167, 173, 179, 181, 191, 193, 197, 199, 211, 223, 227, 229, 233, 239, 241, 251, 257, 263, 269, 271, … (последовательность A008578 в OEIS)
Плоские числа — числа, представимые в виде произведения двух сомножителей, то есть составные:
4, 6, 8, 9, 10, 12, 14, 15, 16, 18, 20, 21, 22, 24, 25, 26, 27, 28, 30, 32, 33, 34, 35, 36, 38, 39, 40, 42, 44, 45, 46, 48, 49, 50, 51, 52, 54, 55, 56, 57, 58, 60, 62, 63, 64, 65, 66, 68, 69, 70, 72, 74, 75, 76, 77, 78, 80, 81, 82, 84, 85, 86, 87, 88, … (последовательность A002808 в OEIS)
- Частным случаем являются прямоугольные числа, являющееся произведением двух последовательных целых чисел, то есть имеющие вид $n(n+1).$
Телесные числа — числа, представимые произведением трёх сомножителей:
8, 12, 16, 18, 20, 24, 27, 28, 30, 32, 36, 40, 42, 44, 45, 48, 50, 52, 54, 56, 60, 63, 64, 66, 68, 70, 72, 75, 76, 78, 80, 81, 84, 88, 90, 92, 96, 98, 99, 100, 102, 104, 105, 108, 110, 112, 114, 116, 117, 120, 124, 125, 126, 128, 130, 132, 135, 136, 138, 140, 144, … (последовательность A033942 в OEIS)
Многоугольные числа — числа, ассоциированные с определённым многоугольником, определение см. ниже.

Классические многоугольные числа

Определение и общий вид

Общее определение^[2]:

$n$ -е по порядку $k$ -угольное число $P_{n}^{(k)}$ есть сумма $n$ членов арифметической прогрессии, у которой первый член есть 1, а разность равна $k-2$ .

Например, треугольные числа получаются как частичные суммы ряда $1+2+3+4\dots$ , а четырёхугольным (квадратным) числам соответствует ряд $1+3+5+7\dots$ .

Последовательность k-угольных чисел имеет вид^[3]:

1,k,3k-3,6k-8,10k-15,15k-24,21k-35,28k-48,36k-63,45k-80\dots n+(k-2){\frac {n(n-1)}{2}}\dots

Другие варианты общего формата представления n-го по порядку $k$ -угольного числа:

P_{n}^{(k)}={\frac {n((k-2)(n-1)+2)}{2}}={\frac {(k-2)n^{2}-(k-4)n}{2}}.

При увеличении числа сторон $k$ на единицу соответствующие фигурные числа изменяются согласно формуле Никомаха^[4]:

P_{n}^{(k+1)}=P_{n}^{(k)}+P_{n-1}^{(3)}

Исторический очерк

Фигурные числа, по мнению пифагорейцев, играют важную роль в структуре мироздания. Поэтому их изучением занимались многие математики античности: Эратосфен, Гипсикл, Диофант Александрийский и другие. Гипсикл (II век до н. э.) дал общее определение m-угольного числа $P_{n}^{(k)}$ как суммы n членов арифметической прогрессии, у которой первый член есть 1, а разность равна $m-2$ . Диофант написал большое исследование о свойствах многоугольных чисел, фрагменты которого дошли до наших дней. О фигурных числах много говорится в пифагорейских учебниках арифметики, созданных Никомахом Геразским и Теоном Смирнским (II век), которые установили ряд зависимостей между фигурными числами разных размерностей. Большой интерес к фигурным числам проявили индийские математики и первые математики средневековой Европы (Фибоначчи, Пачоли, Кардано и др.)^[5].

В Новое время многоугольными числами занимались Ферма, Валлис, Эйлер, Лагранж, Гаусс и другие. Ферма сформулировал в 1637 году так называемую «золотую теорему»^[5]:

Всякое натуральное число — либо треугольное, либо сумма двух или трёх треугольных чисел;
Всякое натуральное число — либо квадратное, либо сумма двух, трёх или четырёх квадратных чисел (Теорема Лагранжа о сумме четырёх квадратов);
Всякое натуральное число — либо пятиугольное, либо сумма от двух до пяти пятиугольных чисел;
и т. д.

Этой теоремой занимались многие выдающиеся математики, полное доказательство сумел дать Коши в 1813 году^[6].

Треугольные числа

Последовательность треугольных чисел:

1, 3, 6, 10, 15, 21, 28, 36, 45, 55, 66, 78, 91, 105, 120, 136, 153, 171, 190, 210, 231, 253, 276, 300, 325, 351, 378, 406, 435, 465, 496, 528, 561, 595, 630, 666, 703, 741, 780, 820, 861, 903, 946, 990, 1035, 1081, 1128, 1176, 1225, 1275, 1326, 1378, 1431, …,

{\frac {n(n+1)}{2}}

, … (последовательность A000217 в OEIS)

Свойства:

Сумма двух последовательных треугольных чисел даёт полный квадрат (квадратное число).
Чётность элемента последовательности меняется с периодом 4: нечётное, нечётное, чётное, чётное.
Ряд из чисел, обратных треугольным, сходится:

1+{1 \over 3}+{1 \over 6}+{1 \over 10}+{1 \over 15}+\dots =2\sum _{n=1}^{\infty }\left({1 \over n}-{1 \over n+1}\right)=2

Всякое чётное совершенное число является треугольным^[7] (и одновременно шестиугольным).

Квадратные числа

1	4	9

Квадратные числа представляют собой произведение двух одинаковых натуральных чисел, то есть являются полными квадратами:

1, 4, 9, 16, 25, 36, 49, 64, 81, 100, 121, 144, 169, 196, 225, 256, 289, 324, 361, 400, 441, 484, 529, 576, 625, 676, 729, 784, 841, 900, 961, 1024, 1089, 1156, 1225, 1296, 1369, 1444, 1521, 1600, 1681, 1764, 1849, 1936, 2025, 2116, 2209, 2304, 2401, 2500, …,

n^{2}

, … (последовательность A000290 в OEIS)

Свойства.

Каждое квадратное число, кроме единицы, есть сумма двух последовательных треугольных чисел:

4=1+3;\quad 9=3+6;\quad 16=6+10

и т. д.

Ряд обратных квадратов сходится:

\sum _{n=1}^{\infty }{\frac {1}{n^{2}}}={\frac {1}{1^{2}}}+{\frac {1}{2^{2}}}+\dots +{\frac {1}{n^{2}}}+\dots ={\frac {\pi ^{2}}{6}}

Гипотеза Лежандра (1808 год, она же третья проблема Э. Ландау): между последовательными квадратными числами всегда найдётся простое число. До сих пор не доказана.

Пятиугольные числа

1, 5, 12, 22, 35, 51, 70, 92, 117, 145, 176, 210, 247, 287, 330, 376, 425, 477, 532, 590, 651, 715, 782, 852, 925, 1001, 1080, 1162, 1247, 1335, 1426, 1520, 1617, 1717, 1820, 1926, 2035, 2147, 2262, 2380, 2501, 2625, 2752, 2882, 3015, 3151, …,

{\frac {n(3n-1)}{2}}

, … (последовательность A000326 в OEIS)

Шестиугольные числа

1, 6, 15, 28, 45, 66, 91, 120, 153, 190, 231, 276, 325, 378, 435, 496, 561, 630, 703, 780, 861, 946, 1035, 1128, 1225, 1326, 1431, 1540, 1653, 1770, 1891, 2016, 2145, 2278, 2415, 2556, 2701, 2850, 3003, 3160, 3321, 3486, 3655, 3828, 4005, 4186, 4371, 4560 …,

2n^{2}-n

, … (последовательность A000384 в OEIS)

Очевидно, последовательность шестиугольных чисел получается из последовательности треугольных чисел вычёркиванием элементов с чётными номерами: $P_{n}^{(6)}=P_{2n-1}^{(3)}$

Двенадцатиугольные числа

Двенадцатиугольные числа вычисляются по формуле $5n^{2}-4n$ :

1, 12, 33, 64, 105, 156, 217, 288, 369, 460, 561, 672, 793, 924, 1065, 1216, 1377, 1548, 1729, 1920, 2121, 2332, 2553, 2784, 3025, 3276, 3537, 3808, 4089, 4380, 4681, 4992, 5313, 5644, 5985, 6336, 6697, 7068, 7449, 7840, 8241, 8652, 9073, 9504, 9945, … (последовательность A051624 в OEIS)

В десятичной системе $n$ -ое двенадцитиугольное число заканчивается на ту же цифру, что и само число $n$ .

Центрированные многоугольные числа

Центрированные полигональные числа

Центрированные полигональные числа — это класс фигурных чисел, каждое сформировано вокруг центральной точки, окружённой слоями многоугольников с постоянным числом сторон. Каждый слой содержит на одну точку больше чем предыдущий., так что начиная со второго слоя каждый слой $k$ -угольного числа содержит на $k$ больше точек, чем предыдущий. Каждая последовательность может быть представлена как треугольное число, умноженное на константу плюс 1. Так, например, центрированные квадратные числа — это учетверённые треугольные числа плюс 1.

Частные случаи центрированных полигональных чисел

Центрированные треугольные числа

Центрированное треугольное число — это центрированное полигональное число, которое представляет треугольник с точкой в центре и все остальные окружающие точки находятся на треугольных слоях. Центрированное треугольное число задается формулой ${\frac {3n^{2}+3n+2}{2}}$ . Первые несколько центрированных треугольных чисел:

1, 4, 10, 19, 31, 46, 64, 85, 109, 136, 166, 199, 235, 274, 316, 361, 409, 460, 514, 571, 631, 694, 760, 829, 901, 976, 1054, 1135, 1219, 1306, 1396, 1489, 1585, 1684, 1786, 1891, 1999, 2110, 2224, 2341, 2461, 2584, 2710, 2839, 2971, …,

{\frac {3n^{2}+3n+2}{2}}

, … (последовательность A005448 в OEIS)

Каждое центрированное треугольное число, начиная с 10, является суммой трех последовательных треугольных чисел. Также, каждое центрированное треугольное число при делении на 3 дает остаток 1 и частное (если оно положительно), есть предыдущее треугольное число. Сумма первых $n$ центрированных треугольных чисел есть магическая константа для магического квадрата $n\times n(n>2)$ .

Центрированные треугольные простые числа

Центрированное треугольное простое — это центрированное треугольное число, являющееся простым. Несколько первых центрированных треугольных простых:

19, 31, 109, 199, 409, … (последовательность A125602 в OEIS).

Центрированные квадратные числа

Центрированное квадратное число — это центрированное полигональное число, которое представляет квадрат с точкой в центре и все остальные окружающие точки находятся на квадратных слоях. Первые несколько центрированных квадратных чисел:

1, 5, 13, 25, 41, 61, 85, 113, 145, 181, 221, 265, 313, 365, 421, 481, 545, 613, 685, 761, 841, 925, 1013, 1105, 1201, 1301, 1405, 1513, 1625, 1741, 1861, 1985, 2113, 2245, 2381, 2521, 2665, 2813, 2965, 3121, 3281, 3445, 3613, 3785, 3961, 4141, 4325, …,

n^{2}+(n-1)^{2}

, … (последовательность A001844 в OEIS)

Формулу можно представить следующим образом

C_{4,n}={(2n-1)^{2}+1 \over 2}

;

таким образом, n-ое центрированное квадратное число равно половине $n$ -го нечетного квадрата + 1/2. Как и другие центрированные полигональные числа, центрированные квадратные числа могут быть выражены в треугольных числах:

C_{4,n}=1+4\,T_{n-1}

,

где

T_{n}

есть $n$ -ое треугольное число. Центрированное квадратное число — это сумма двух последовательных квадратов. Все центрированные квадратные числа нечетны, и последняя цифра в десятичном представлении дает последовательность 1-5-3-5-1.Все центрированные квадратные числа и их делители дают остаток 1 при делении на 4. Отсюда все центрированные квадратные числа и их делители сравнимы с 1 или 5 по модулю 6,8 или 12. Все центрированные квадратные числа за исключением 1 есть гипотенуза в одном из пифагоровой тройке (например, 3-4-5, 5-12-13). Таким образом, каждое центрированное квадратное число равно числу точек внутри данного расстояния в кварталах от центральной точки на квадратной решетке. Разность между двумя последовательными восьмиугольными числами есть центрированное квадратное число.

Центрированные квадратные простые числа

Центрированные квадратные простые — это центрированные квадратные числа, являющиеся также простыми. В отличие от обычных квадратных чисел, которые никогда не являются простыми, несколько центрированных квадратных чисел просты. Несколько первых центрированных квадратных простых:

5, 13, 41, 61, 113, 181, 313, 421, 613, 761, 1013, 1201, 1301, 1741, 1861, 2113, 2381, 2521, 3121, 3613, … (последовательность A027862 в OEIS). Замечательный пример можно увидеть в магическом квадрате 10-го столетия ал-Антаакии.

Центрированные пятиугольные числа

Центрированное пятиугольное число — это центрированное фигурное число, которое представляет пятиугольник, который содержит точку в центре и все точки, окружающие центр лежат в пятиугольных слоях. Центрированное пятиугольное число задается формулой ${\frac {5(n-1)^{2}+5(n-1)+2}{2}}$ . Несколько первых центрированных пятиугольных чисел:

1, 6, 16, 31, 51, 76, 106, 141, 181, 226, 276, 331, 391, 456, 526, 601, 681, 766, 856, 951, 1051, 1156, 1266, 1381, 1501, 1626, 1756, 1891, 2031, 2176, 2326, 2481, 2641, 2806, 2976, …,

{\frac {5(n-1)^{2}+5(n-1)+2}{2}}

, … (последовательность A005891 в OEIS)

Четность центрированных пятиугольных чисел подчиняется правилу четное-четное-нечетное -нечетное, и последняя десятичная цифра подчиняется правилу 6-6-1-1.

Центрированные шестиугольные числа

Центрированные шестиугольные числа — это центрированные фигурные числа, которые представляют шестиугольник с точкой в центре и все остальные окружающие точки находятся в шестиугольной решётке. Центрированное шестиугольное число задается формулой $n^{3}-(n-1)^{3}=3n(n-1)+1$ . Несколько первых центрированных шестиугольных чисел:

1, 7, 19, 37, 61, 91, 127, 169, 217, 271, 331, 397, 469, 547, 631, 721, 817, 919, …,

1+6\left({1 \over 2}n(n-1)\right)

, …(последовательность A003215 в OEIS)

Можно заметить, что по основанию 10 последний знак центрированных шестиугольных чисел имеют последовательность 1-7-9-7-1. Сумма первых n центрированных шестиугольных чисел равна $n^{3}$ . Таким образом, центрированные шестиугольные пирамидальные числа и кубы являются те ми числами, но представляют различные (геометрические) формы. С другой стороны, центрированные шестиугольные числа — это разность двух соседних кубов, так что центрированные шестиугольные числа — это фигурное представление кубов. Также, простые центрированные шестиугольные числа есть кубические простые числа. Также $(2n)^{2}-C_{6,n}=3n^{2}+3n-1$ .

Центрированные семиугольные числа

Центрированное семиугольное число — это центрированное фигурное число, которое представляет семиугольник с точкой в середине и все окружающие точки лежат на семиугольных слоях. Центрированное семиугольное число задается формулой ${\frac {7n^{2}-7n+2}{2}}$ . Его можно также вычислить умножением треугольного числа $(n-1)$ на 7, затем добавив 1. Несколько первых центрированных семиугольных чисел:

1, 8, 22, 43, 71, 106, 148, 197, 253, 316, 386, 463, 547, 638, 736, 841, 953, …,

{\frac {7n^{2}-7n+2}{2}}

, … (последовательность A069099 в OEIS)

Четность центрированных семиугольных чисел меняется по правилу нечетный-четный-четный-нечетный.

Центрированные семиугольные простые числа

Центрированные семиугольные простые — это центрированные семиугольные числа, являющиеся простыми. Несколько первых центрированных семиугольных простых:

43, 71, 197, 463, 547, 953, 1471, 1933, 2647, 2843, 3697, … (последовательность A144974 в OEIS)

и центрированных семиугольных простых простых-близнецов:

43, 71, 197, 463, 1933, 5741, 8233, 9283, 11173, 14561, 34651, … (последовательность A144975 в OEIS)

Центрированные восьмиугольные числа

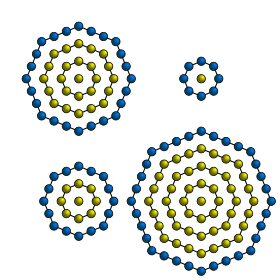
Центрированное восьмиугольное число — это центрированное фигурное число, которое представляет восьмиугольник с точкой в середине и все окружающие точки лежат на восьмиугольных слоях. Центрированное восьмиугольное число задается формулой $(2n-1)^{2}=4n^{2}-4n+1$ . Несколько первых центрированных восьмиугольных чисел:

1, 9, 25, 49, 81, 121, 169, 225, 289, 361, 441, 529, 625, 729, 841, 961, 1089.

Все центрированные восьмиугольные числа нечетны, и по модулю 10 имеют последовательность остатков 1-9-5-9-1. Нечетное число является центрированным восьмиугольным числом тогда и только тогда, когда оно является квадратом целого числа.

Центрированные девятиугольные числа

Центрированное девятиугольное число — это центрированное фигурное число, которое представляет девятиугольник с точкой в середине и все окружающие точки лежат на девятиугольных слоях. Умножая $(n-1)$ -ое треугольное число на 9 и добавляя 1 получим $n$ -ое центрированное девятиугольное число, но имеется и более простая связь с треугольными числами — каждое третье треугольное число (1-е, 4-е, 7-е, и т. д.) также центрированное девятиугольное число. Первые несколько центрированных девятиугольных чисел:

1, 10, 28, 55, 91, 136, 190, 253, 325, 406, 496, 595, 703, 820, 946, … (последовательность A060544 в OEIS)

За исключением 6, все четные совершенные числа являются также центрированными девятиугольными числами. В 1850-м году, Поллок высказал предположение, что любое натуральное есть сумма максимум одиннадцати центрированных девятиугольных чисел, которое ни доказано ни опровергнуто.

Центрированные десятиугольные числа

Центрированное десятиугольное число — это центрированное фигурное число, которое представляет десятиугольник с точкой в середине и все окружающие точки лежат на десятиугольных слоях. Центрированное десятиугольное число задается формулой $5(n^{2}-n)+1$ . Первые несколько центрированных десятиугольных чисел:

1, 11, 31, 61, 101, 151, 211, 281, 361, 451, 551, 661, 781, 911, 1051, …,

5(n^{2}-n)+1

, … (последовательность A062786 в OEIS)

Подобно другим $k$ -угольным числам, $n$ -ое центрированное десятиугольное число можно вычислить, умножая $(n-1)$ -ое треугольное число на $k$ , в нашем случае 10, затем добавляя 1. Как следствие, центрированные десятиугольные числа могут быть получены просто добавлением 1 к десятичному представлению числа. Таким образом, все центрированные десятиугольные числа нечётны и всегда оканчиваются на 1 в десятичном представлении. Заметьте, что следующие совершенные числа встречаются в списке:

3-е центрированное девятиугольное число есть

7\times 8\div 2=28

, и 11-е есть

31\times 32\div 2=496

.

Далее: 43-е есть

127\times 128\div 2=8128

и 2731-е есть

8191\times 8192\div 2=33\,550\,336

.

За исключением 6, все четные совершенные числа являются также центрированными девятиугольными числами, по формуле

Nc\left({\frac {2^{p}+1}{3}}\right)=2^{p-1}(2^{p}-1)

, где

2^{p}-1

— простые числа Мерсена.

Центрированные десятиугольные простые числа

Центрированные десятиугольные простые — это центрированное десятиугольное число, которое является простым. Несколько первых центрированных десятиугольных простых:

11, 31, 61, 101, 151, 211, 281, 661, 911, 1051, 1201, 1361, 1531, 1901, 2311, 2531, 3001, 3251, 3511, 4651, 5281, …. (последовательность A090562 в OEIS)

Многомерные фигурные числа

Можно определить многомерные фигурные числа, частными случаями которых являются:

Изоэдральные многомерные фигурные числа. Пример: последовательность A081436 в OEIS.
Элементарные многомерные фигурные числа:
- Гиперкубические: $A_{n}^{k}=n^{k}$
- Симплексные: $P_{n}^{k}={\tbinom {n-1+k}{k}}={\tfrac {(n-1+k)!}{(n-1)!k!}}$ . В частности, $P_{n}^{2}$ — это треугольные числа, $P_{n}^{3}$ — тетраэдрические числа.
- Гипероктаэдрные: $T_{n}^{k}=T_{n}^{k-1}+T_{n-1}^{k}+T_{n-1}^{k-1}$ , где $T_{n}^{1}=n$ . Пример: последовательность A014820 в OEIS.
Трёхмерные правильные фигурные числа:
$P_{n}^{3}=n+(e-2){\frac {n(n-1)}{2}}+(f-m)(k-2){\frac {n(n-1)(n-2)}{6}},$

где e — число вершин многогранника, f — число его граней, k — число сторон каждой грани, m — число граней, примыкающих к каждой вершине. Примеры: последовательности A006566, A006564, A005900.

Четырехмерные правильные фигурные числа:
$P_{n}^{4}=n+(E-2){\frac {n(n-1)}{2}}+(G-{\frac {m_{f}}{2}})(f-m)(k-2){\frac {n(n-1)(n-2)}{6}}+(G-m_{f})(f-m)(k-2){\frac {n(n-1)(n-2)(n-3)}{24}},$

где E — число вершин, G — число граней

m_{f}

— число многогранных углов вершины. Примеры: последовательности A092182, A092181, A092183.

Трёхмерные правильные фигурные числа

Тетраэдрические числа

Тетраэдр с длиной стороны 5 содержит 35 сфер. Каждый слой представляет одно из первых пяти треугольных чисел.

Тетраэдрические числа — это фигурные числа, которые представляют пирамиду, в основании которой лежит треугольник. Пример нескольких первых тетраэдрических чисел:

1, 4, 10, 20, 35, 56, 84, 120, 165, 220, 286, 364, 455, 560, 680, 816, 969, … (последовательность A000292 в OEIS)

Формула

Формула для тетраэдрического числа:

{\frac {n(n+1)(n+2)}{6}}

Свойства

Тетраэдрические числа находятся на 4-й позиции в треугольнике Паскаля. $n$ -ое тетраэдрическое число представляет собой сумму первых $n$ треугольных чисел. Только три тетраэдрических числа являются квадратными числами:

1^{2}=1

,

2^{2}=4

,

140^{2}=19\,600

.

Пять чисел являются треугольными (последовательность A027568 в OEIS):

1, 10, 120, 1540, 7140.

Можно заметить, что:

T_{5}=T_{4}+T_{3}+T_{2}+T_{1}

.

Квадратные пирамидальные числа

В математике пирамида́льное число́ или квадра́тное пирамида́льное число́ — фигурное число, представляющее собой количество сложенных сфер в пирамиде с квадратным основанием. Квадратные пирамидальные числа также выражают количество квадратов в сетке $N\times N$ . Квадратные пирамидальные числа образуют последовательность:

1, 5, 14, 30, 55, 91, 140, 204, 285, 385, 506, 650, 819, … (последовательность A000330 в OEIS).

Формула

Квадратные пирамидальные числа могут быть вычислены по формуле:

{\frac {n(n+1)(2n+1)}{6}}={\frac {2n^{3}+3n^{2}+n}{6}}

.

См. также

Последовательность

Примечания

↑ Гайденко П. П. Эволюция понятия науки (становление и развитие первых научных программ), глава 1. М.: Наука, 1980.
↑ Ожигова Е. П. Что такое теория чисел. — М.: Знание, 1970. — С. 56—57.
↑ Арифметический ряд // Математическая энциклопедия (в 5 томах). — М.: Советская Энциклопедия, 1982. — Т. 1.
↑ За страницами учебника математики, 1996, с. 50.
1 2 Матвиевская Г. П. Учение о числе на средневековом Ближнем и Среднем Востоке. — Ташкент: ФАН, 1967. — С. 22—23. — 344 с. Вопреки названию, книга прослеживает историю понятия числа с самых древних времён.
↑ Виленкин Н. Я. Популярная комбинаторика. — М.: Наука, 1975. — С. 10-11. — 208 с.
↑ За страницами учебника математики, 1996, с. 51.

Литература

Виленкин Н. Я., Шибасов Л. П. Шибасова 3. Ф. За страницами учебника математики: Арифметика. Алгебра. Геометрия. — М.: Просвещение, 1996. — С. 30. — 320 с. — ISBN 5-09-006575-6.
Глейзер Г. И. История математики в школе. — М.: Просвещение, 1964. — 376 с.
Депман И. Я. История арифметики. Пособие для учителей. — Изд.второе. — М.: Просвещение, 1965. — С. 150—155.
Матвиевская Г. П. Заметки о многоугольных числах в записных книжках Эйлера // Историко-математические исследования. — М.: Наука, 1983. — № 27. — С. 27-49.
Серпинский В. Пифагоровы треугольники. — М.: Учпедгиз, 1959. — 111 с.
Стиллвелл Д. Глава 3. Греческая теория чисел // Математика и её история. — Москва-Ижевск: Институт компьютерных исследований, 2004.

Ссылки

Figurate Numbers на сайте MathWorld (англ.)

Данная страница на сайте WikiSort.ru содержит текст со страницы сайта "Википедия".

Если Вы хотите её отредактировать, то можете сделать это на странице редактирования в Википедии.

Если сделанные Вами правки не будут кем-нибудь удалены, то через несколько дней они появятся на сайте WikiSort.ru .

Текст в блоке "Читать" взят с сайта "Википедия" и доступен по лицензии Creative Commons Attribution-ShareAlike; в отдельных случаях могут действовать дополнительные условия.

Другой контент может иметь иную лицензию. Перед использованием материалов сайта WikiSort.ru внимательно изучите правила лицензирования конкретных элементов наполнения сайта.

2019-2024
WikiSort.ru - проект по пересортировке и дополнению контента Википедии

[1] Гайденко П. П. Эволюция понятия науки (становление и развитие первых научных программ), глава 1. М.: Наука, 1980.

[2] Ожигова Е. П. Что такое теория чисел. — М.: Знание, 1970. — С. 56—57.

[3] Арифметический ряд // Математическая энциклопедия (в 5 томах). — М.: Советская Энциклопедия, 1982. — Т. 1.

[_f26532716c1a07da-4] За страницами учебника математики, 1996, с. 50.

[MATV-5] 1 2 Матвиевская Г. П. Учение о числе на средневековом Ближнем и Среднем Востоке. — Ташкент: ФАН, 1967. — С. 22—23. — 344 с. Вопреки названию, книга прослеживает историю понятия числа с самых древних времён.

[6] Виленкин Н. Я. Популярная комбинаторика. — М.: Наука, 1975. — С. 10-11. — 208 с.

[_f26532716c1a07db-7] За страницами учебника математики, 1996, с. 51.