Квадра́тное уравне́ние — алгебраическое уравнение общего вида
где — неизвестное, , , — коэффициенты, причём
Выражение называют квадратным трёхчленом[1].
Корень — это значение переменной , обращающее квадратный трёхчлен в ноль, а квадратное уравнение в верное числовое равенство.
Элементы квадратного уравнения имеют собственные названия[1]:
- называют первым или старшим коэффициентом,
- называют вторым, средним или коэффициентом при ,
- называют свободным членом.
Приведённым называют квадратное уравнение, в котором старший коэффициент равен единице[1]. Такое уравнение может быть получено делением всего выражения на старший коэффициент :
Полным называют такое квадратное уравнение, все коэффициенты которого отличны от нуля.
Неполным называется такое квадратное уравнение, в котором хотя бы один из коэффициентов, кроме старшего (либо второй коэффициент, либо свободный член), равен нулю.
Исторические сведения о квадратных уравнениях
Древний Вавилон
Уже во втором тысячелетии до нашей эры вавилоняне знали, как решать квадратные уравнения[1]. Решение их в Древнем Вавилоне было тесно связано с практическими задачами, в основном такими, как измерение площади земельных участков, земельные работы, связанные с военными нуждами; наличие этих познаний также обусловлено развитием математики и астрономии вообще. Были известны способы решения как полных, так и неполных квадратных уравнений. Приведём примеры квадратных уравнений, решавшихся в Древнем Вавилоне, используя современную алгебраическую запись:
Правила решения квадратных уравнений во многом аналогичны современным, однако в вавилонских текстах не зафиксированы рассуждения, путём которых эти правила были получены.
Индия
Задачи, решаемые с помощью квадратных уравнений, встречаются в трактате по астрономии «Ариабхаттиам», написанным индийским астрономом и математиком Ариабхатой в 499 году нашей эры. Один из первых известных выводов формулы корней квадратного уравнения принадлежит индийскому учёному Брахмагупте (около 598 г.)[1]; Брахмагупта изложил универсальное правило решения квадратного уравнения, приведённого к каноническому виду: ; притом предполагалось, что в нём все коэффициенты, кроме могут быть отрицательными. Сформулированное учёным правило по своему существу совпадает с современным.
Корни квадратного уравнения на множестве действительных чисел
I способ. Общая формула для вычисления корней
Для нахождения корней квадратного уравнения в общем случае следует пользоваться приводимым ниже алгоритмом:
| Условие | |||
| Число действительных корней | корней два | корень один (в некоторых контекстах говорят также о двух равных или совпадающих корнях — его, к тому же, называют корнем кратности 2) | делают вывод о том, что корней на множестве действительных чисел нет. |
| Формула | формулу комплексных корней смотрите ниже в соотв. разделе |
Формулу можно получить следующим образом:
Умножаем каждую часть на и прибавляем :
Примечание: очевидно, что формула для корня кратности 2 является частным случаем общей формулы, получается при подстановке в неё равенства D=0, а вывод о отсутствии вещественных корней при D<0 следует также сделать, учтя, что в этом случае -D>0, а .
Изложенный метод универсален, однако он далеко не единственный.
II способ. Корни квадратного уравнения при чётном коэффициенте b
Для уравнений вида , то есть при чётном , где
вместо формулы (1) для нахождения корней можно использовать более простые выражения[1].
Примечание: данные ниже формулы можно получить, подставив в стандартные формулы выражение b=2k и совершив при этом несложные преобразования.
| неприведённое | приведённое | D>0 | неприведённое | приведённое |
| удобнее вычислять значение
четверти дискриминанта: Все необходимые свойства при этом сохраняются. |
. | |||
| D=0 | ||||
III способ. Решение неполных квадратных уравнений
К решению неполных квадратных уравнений следует подходить по-особому. Рассмотрим три возможных ситуации.
|
|
Если , то уравнение имеет два действительных корня, a если , то уравнение не имеет действительных корней. |
или Такое уравнение обязательно имеет два действительных корня |
IV способ. Использование частных соотношений коэффициентов
Существуют частные случаи квадратных уравнений, в которых коэффициенты находятся в соотношениях между собой, позволяющих решать их гораздо проще.
Корни квадратного уравнения, в котором сумма старшего коэффициента и свободного члена равна второму коэффициенту
Если в квадратном уравнении сумма первого коэффициента и свободного члена равна второму коэффициенту: , то его корнями являются и число, противоположное отношению свободного члена к старшему коэффициенту ( ).
Способ 1. Сначала выясним, действительно ли такое уравнение имеет два корня (в том числе, два совпадающих):
- .
Да, это так, ведь при любых действительных значениях коэффициентов , а значит и дискриминант неотрицателен. Таким образом, если , то уравнение имеет два корня, если же , то оно имеет только один корень. Найдём эти корни:
- .
В частности, если , то корень будет один:
Способ 2.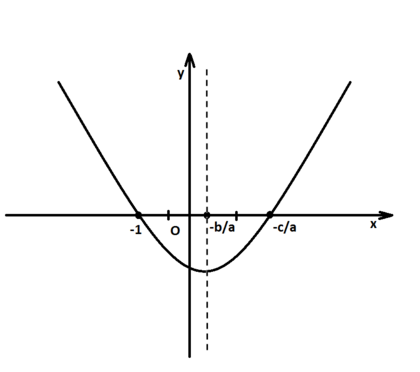
Используем геометрическую модель корней квадратного уравнения: их мы будем рассматривать как точки пересечения параболы с осью абсцисс. Всякая парабола вне зависимости от задающего её выражения является фигурой, симметричной относительно прямой . Это означает, что отрезок всякой перпендикулярной к ней прямой, отсекаемый на ней параболой, делится осью симметрии пополам. Сказанное, в частности, верно и для оси абсцисс. Таким образом, для всякой параболы справедливо одно из следующих равенств: (если ) или (если верно неравенство противоположного смысла). Используя тождество , выражающее геометрический смысл модуля, а также принимая, что (это можно доказать, подставив равенство в квадратный трёхчлен: , поэтому -1 - корень такого уравнения) , приходим к следующему равенству: Если учитывать, что разность в том случае, когда мы прибавляем модуль, всегда положительна, а в том, когда отнимаем - отрицательна, что говорит о тождественности этих случаев, и, к тому же, помня о равенстве , раскрываем модуль: . Во втором случае,совершив аналогичные преобразования, придём к тому же результату, ч.т.д.
- Отсюда, прежде, чем решать какое-либо квадратное уравнение, следует проверить возможность применения к нему этой теоремы: сравнить сумму старшего коэффициента и свободного члена со вторым коэффициентом.
Корни квадратного уравнения, сумма всех коэффициентов которого равна нулю
Если в квадратном уравнении сумма всех его коэффициентов равна нулю ( ), то корнями такого уравнения являются и отношение свободного члена к старшему коэффициенту ( ).
Способ 1. Прежде всего заметим, что из равенства следует, что Установим количество корней:
При любых значениях коэффициентов уравнение имеет хотя бы один корень: действительно, ведь при любых значениях коэффициентов , а значит и дискриминант неотрицателен. Обратите внимание, что если , то уравнение имеет два корня, если же , то только один. Найдём эти корни:
что и требовалось доказать.
- В частности, если , то уравнение имеет только один корень, которым является число .
Способ 2. Пользуясь данным выше определением корня квадратного уравнения, обнаруживаем путём подстановки, что число 1 является таковым в рассматриваемом случае: - верное равенство, следовательно, единица - корень такого вида квадратных уравнений. Далее, по теореме Виета находим второй корень: согласно этой теореме, произведение корней уравнения равно числу, равному отношению свободного члена к старшему коэффициенту - , ч.т.д.
- Отсюда, прежде, чем решать уравнение стандартными методами, следует проверить применимость к нему этой теоремы: сложить все коэффициенты данного уравнения и посмотреть, не равна ли нулю эта сумма.
V способ. Разложение квадратного трёхчлена на линейные множители
Если трёхчлен вида удастся каким-либо образом представить в качестве произведения линейных множителей , то можно найти корни уравнения — ими будут и , действительно, ведь , а решив указанные линейные уравнения, получим вышеописанное. Отметим, что квадратный трёхчлен не всегда раскладывается на линейные множители с действительными коэффициентами: это возможно, если соответствующее ему уравнение имеет действительные корни.
Рассмотрим некоторые частные случаи.
Использование формулы квадрата суммы (разности)
Если квадратный трёхчлен имеет вид , то применив к нему названную формулу, мы сможем разложить его на линейные множители и, значит, найти корни:
Выделение полного квадрата суммы (разности)
Также названную формулу применяют, пользуясь методом, получившим названия «выделение полного квадрата суммы (разности)». Применительно к приведённому квадратному уравнению с введёнными ранее обозначениями, это означает следующее:
- прибавляют и отнимают одно и то же число
. - применяют формулу к полученному выражению, переносят вычитаемое и свободный член в правую часть
- извлекают из левой и правой частей уравнения квадратный корень и выражают переменную
Примечание: если вы заметили, данная формула совпадает с предлагаемой в разделе «Корни приведённого квадратного уравнения», которую, в свою очередь, можно получить из общей формулы (1) путём подстановки равенства a=1. Этот факт не просто совпадение: описанным методом, произведя, правда, некоторые дополнительные рассуждения, можно вывести и общую формулу, а также доказать свойства дискриминанта.
VI способ. Использование прямой и обратной теоремы Виета
Прямая теорема Виета (см. ниже в одноимённом разделе) и обратная ей теорема позволяют решать приведённые квадратные уравнения устно, не прибегая к вычислениям по формуле (1).
Согласно обратной теореме, всякая пара чисел (число) , будучи решением нижеприведённой системы уравнений, являются корнями уравнения :
Подобрать устно числа, удовлетворяющие этим уравнениям, поможет прямая теорема. С её помощью можно определить знаки корней, не зная сами корни. Для этого следует руководствоваться правилом:
- 1) если свободный член отрицателен, то корни имеют различный знак, и наибольший по модулю из корней — знак, противоположный знаку второго коэффициента уравнения;
- 2) если свободный член положителен, то оба корня обладают одинаковым знаком, и это — знак, противоположный знаку второго коэффициента.
VII способ. Метод «переброски»
Так называемый метод «переброски» позволяет сводить решение неприведённых и непреобразуемых к виду приведённых с целыми коэффициентами путём их деления на старший коэффициент уравнений к решению приведённых с целыми коэффициентами. Он заключается в следующем:
- 1) умножаем обе части на выражение:
- 2) вводим новую переменную y=ax:
- .
Далее уравнение решают устно описанным выше способом, затем возвращаются к исходной переменной и находят корни уравнений и .
Допустим, мы желаем решить с использованием обратной теоремы Виета уравнение . Если мы попробуем разделить обе его части на 8, то получим приведённое уравнение с дробными коэффициентами, поэтому применить к нему теорему будет трудно. Однако, воспользовавшись методом переброски, мы сумеем получить приведённое с целыми коэффициентами:
- .
Совершив замену переменной по формуле y=8x, придём к уравнению:
- .
Очевидно, что его корнями будут числа -4 и 2. Произведём обратную замену:
Геометрический смысл
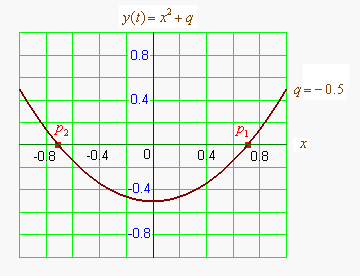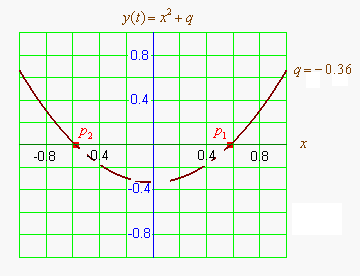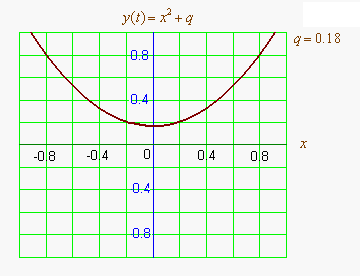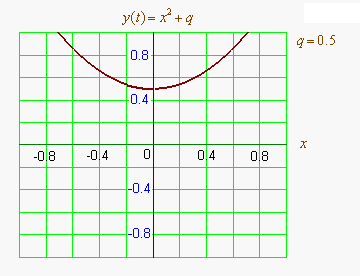
Графиком квадратичной функции является парабола. Решениями (корнями) квадратного уравнения называют абсциссы точек пересечения параболы с осью абсцисс. Если парабола, описываемая квадратичной функцией, не пересекается с осью абсцисс, уравнение не имеет вещественных корней. Если парабола пересекается с осью абсцисс в одной точке (в вершине параболы), уравнение имеет один вещественный корень (также говорят, что уравнение имеет два совпадающих корня). Если парабола пересекает ось абсцисс в двух точках, уравнение имеет два вещественных корня (см. изображение справа.)
Если коэффициент положительный, ветви параболы направлены вверх и наоборот. Если коэффициент положительный (при положительном , при отрицательном наоборот), то вершина параболы лежит в левой полуплоскости и наоборот.
Графический способ решения квадратных уравнений
Помимо универсального способа, описанного выше, существует так называемый графический способ. В общем виде этот способ решения рационального уравнения вида заключается в следующем: в одной системе координат строят графики функций и и находят абсциссы общих точек этих графиков; найденные числа и будут корнями уравнения.
- Есть всего пять основных способов графического решения квадратных уравнений.
Способ I
Для решения квадратного уравнения этим способом строится график функции и отыскивается абсциссы точек пересечения такого графика с осью .
Способ II
Для решения того же уравнения этим способом его преобразуют к виду и строят в одной системе координат графики квадратичной функции и линейной функции , затем находят абсциссу точек их пересечения.
Способ III
Решение этим методом подразумевает преобразование исходного уравнения к виду , используя метод выделения полного квадрата суммы (разности) и затем в . После этого строятся график функции (им является график функции , смещённый на единиц масштаба вправо или влево в зависимости от знака) и прямую , параллельную оси абсцисс. Корнями уравнения будут абсциссы точек пересечения параболы и прямой.
Способ IV
Квадратное уравнение преобразуют к виду , строят график функции (им является график функции , смещённый на единиц масштаба вверх, если этот коэффициент положителен, либо вниз если он отрицателен), и , находят абсциссы их общих точек.
Способ V
Квадратное уравнение преобразуют к особому виду:
затем
- .
Совершив преобразования, строят графики линейной функции и обратной пропорциональности , отыскивают абсциссы точек пересечения этих графиков. Этот метод имеет границу применимости: если , то метод не используется.
Решение квадратных уравнений с помощью циркуля и линейки
Описанные выше методы графического решения имеют существенные недостатки: они достаточно трудоёмки, при этом точность построения кривых — парабол и гипербол — низка. Указанные проблемы не присущи предлагаемому ниже методу, предполагающему относительно более точные построения циркулем и линейкой.
Чтобы произвести такое решение, нужно выполнить нижеследующую последовательность действий.
- Построить в системе координат Oxy окружность с центром в точке , пересекающую ось y в точке C(0;1).
- Далее возможны три случая:
- длина радиуса окружности превышает длину перпендикуляра к оси абсцисс, опущенного из точки S: в этом случае окружность пересекает ось x в двух точках, а уравнение имеет два действительных корня, равных абсциссам этих точек;
- радиус равен перпендикуляру: одна точка и один вещественный корень кратности 2;
- радиус меньше перпендикуляра: корней в множестве нет.

Рассматриваемый способ предполагает построение окружности, пересекающей ось ординат в точках (точке), абсциссы которых являются корнями (или корнем) решаемого уравнения. Как нужно строить такую окружность? Предположим, что она уже построена. Окружность определяется однозначно заданием трёх своих точек. Пусть в случае, если корня два, это будут точки , где , естественно, действительные корни квадратного уравнения (подчёркиваем: если они имеются). Найдём координаты центра такой окружности. Для этого докажем, что эта окружность проходит через точку . Действительно, согласно теореме о секущих, в принятых обозначениях выполняется равенство (см рисунок). Преобразовывая это выражение, получаем величину отрезка OD, которой и определяется искомая ордината точки D: (в последнем преобразовании использована теорема Виета (см. ниже в одноимённом разделе)). Если же корень один, то есть ось абсцисс будет касательной к такой окружности, и окружность пересекает ось y в точке с ординатой 1, то она обязательно пересечёт её и в точке с указанной выше ординатой (в частности, если 1=c/a, это могут быть совпадающие точки), что доказывается аналогично с использованием уже теоремы о секущей и касательной, являющаяся частным случаем теоремы о секущих. В первом случае ( ), определяющими будут точка касания, точка оси y с ординатой 1, и её же точка с ординатой . Если c/a и 1 - совпадающие точки, а корня два, определяющими будут эта точка и точки пересечения с осью абсцисс. В случае, когда (1=c/a) и корень один, указанных сведений достаточно для доказательства, так как такая окружность может быть только одна - её центром будет вершина квадрата, образуемого отрезками касательных и перпендикулярами, а радиус - стороне этого квадрата, составляющей 1. Пускай S - центр окружности, имеющей с осью абсцисс две общие точки. Найдём его координаты: для этого опустим от этой точки перпендикуляры к координатным осям. Концы этих перпендикуляров будут серединами отрезков AB и CD - ведь треугольники ASB и CSD равнобедренные, так как в них AS=BS=CS=DS как радиусы одной окружности, следовательно, высоты в них, проведённые к основаниям, также являются и медианами. Найдём координаты середин названных отрезков. Так как парабола симметрична относительно прямой , то точка этой прямой с такой же абсциссой будет являться серединой отрезка AB. Следовательно, абсцисса точки S равна этому числу. В случае же, если уравнение имеет один корень, то ось x является касательной по отношению к окружности,поэтому, согласно её свойству, её радиус перпендикулярен оси, следовательно, и в этом случае указанное число - абсцисса центра. Её ординату найдём так: . В третьем из возможных случаев, когда c\a=1 (и, значит, a=c), то .
Итак, нами найдены необходимые для построения данные. Действительно, если мы построим окружность с центром в точке , проходящую через точку , то она, в случаях, когда уравнение имеет действительные корни, пересечёт ось x в точках, абсциссы которых есть эти корни. Причём, если длина радиуса больше длины перпендикуляра к оси Ox, то уравнение имеет два корня (предположив обратное, мы бы получили противоречие с доказанным выше), если длины равны, то один (по той же причине), если же длина радиуса меньше длины перпендикуляра, то окружность не имеет общих точек с осью x, следовательно, и действительных корней у уравнения нет (доказывается тоже от противного: если корни есть, то окружность, проходящая через A, B, C совпадает с данной, и поэтому пересекает ось, однако она не должна пересекать ось абсцисс по условию, значит, предположение неверно).
Корни квадратного уравнения на множестве комплексных чисел
Уравнение с действительными коэффициентами
Квадратное уравнение с вещественными коэффициентами имеет ровно два комплексных корня, о чём гласит основная теорема алгебры. При этом, в зависимости от значения дискриминанта , как один, так и оба корня могут не иметь мнимой части и быть вещественными:
- при
вещественных корней два, и они вычисляются по формуле
- при
корень один (о чём так же можно говорить как о двух равных или совпадающих корнях), кратности 2:
- при
вещественных (действительных) корней нет, однако существуют два комплексных корня, выражающиеся той же формулой, что и для положительного дискриминанта. Также её можно переписать, выразив корень из отрицательного числа в виде произведения корня с мнимой единицей:
Уравнение с комплексными коэффициентами
В комплексном случае квадратное уравнение решается по той же формуле (1) и указанным выше её вариантам, но различимыми являются только два случая: нулевого дискриминанта (один двукратный корень) и ненулевого (два простых корня).
Корни приведённого квадратного уравнения
Квадратное уравнение вида в котором старший коэффициент равен единице, называют приведённым. В этом случае формула для корней (1) упрощается до
Мнемонические правила:
- Из «Радионяни»:
«Минус» напишем сначала,
Рядом с ним p пополам,
«Плюс-минус» знак радикала,
С детства знакомого нам.
Ну, а под корнем, приятель,
Сводится всё к пустяку:
p пополам и в квадрате
Минус прекрасное[2] q.
- Из «Радионяни» (другой вариант):
p, со знаком взяв обратным,
На два мы его разделим,
И от корня аккуратно
Знаком «минус-плюс» отделим.
А под корнем очень кстати
Половина p в квадрате
Минус q — и вот решенья,
То есть корни уравненья.
Теорема Виета
Формулировка
Сумма корней приведённого квадратного уравнения равна коэффициенту со знаком «минус», а произведение корней равно свободному члену
В общем случае, то есть для не приведённого квадратного уравнения :
Используя эту теорему, можно решать некоторые квадратные уравнения устно.
Разложение квадратного трёхчлена на множители и теоремы, следующие из этого
Если известны оба корня квадратного трёхчлена, его можно разложить по формуле
- (2)
Доказательство
Для доказательства этого утверждения воспользуемся теоремой Виета. Согласно этой теореме, корни и квадратного уравнения образуют соотношения с его коэффициентами: . Подставим эти соотношения в квадратный трёхчлен:
- .
В случае нулевого дискриминанта это соотношение становится одним из вариантов формулы квадрата суммы или разности.
- Из формулы (2) имеются два важных следствия:
Следствие 1
- Если квадратный трёхчлен раскладывается на линейные множители с вещественными коэффициентами, то он имеет вещественные корни.
Доказательство
Пусть . Тогда, переписав это разложение, получим:
- .
Сопоставив полученное выражение с формулой (2), находим, что корнями такого трёхчлена являются и . Так как коэффициенты вещественны, то и числа, противоположные их отношениям также являются элементами множества .
Следствие 2
- Если квадратный трёхчлен не имеет вещественных корней, то он не раскладывается на линейные множители с вещественными коэффициентами.
Доказательство
Действительно, если мы предположим противное (что такой трёхчлен раскладывается на линейные множители), то, согласно следствию 1, он имеет корни в множестве , что противоречит условию, а потому наше предположение неверно, и такой трёхчлен не раскладывается на линейные множители.
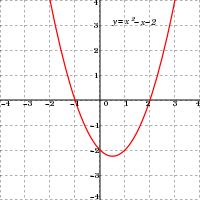
f (x) = x2 − x − 2 = (x + 1)(x − 2) действительной переменной x, x — координаты точки, где график пересекает ось x-ов, x = −1 и x = 2, являются решениями квадратного уравнения: x2 − x − 2 = 0.
Уравнения, сводящиеся к квадратным
Алгебраические
Уравнение вида является уравнением, сводящимся к квадратному.
В общем случае оно решается заменой c последующим решением квадратного уравнения .
Также при решении можно обойтись без замены, решив совокупность двух уравнений:
- и
Если , то уравнение принимает вид:
Такое уравнение называется биквадратным[3][1].
С помощью замены
к квадратному уравнению сводится уравнение
известное как возвратное или обобщённо-симметрическое уравнение[1].
Дифференциальные
Линейное однородное дифференциальное уравнение с постоянными коэффициентами второго порядка
подстановкой сводится к характеристическому квадратному уравнению:
Если решения этого уравнения и не равны друг другу, то общее решение имеет вид:
- , где и — произвольные постоянные.
Для комплексных корней можно переписать общее решение, используя формулу Эйлера:
Если решения характеристического уравнения совпадают , общее решение записывается в виде:
Уравнения такого типа часто встречаются в самых разнообразных задачах математики и физики, например, в теории колебаний или теории цепей переменного тока.
Примечания
Литература
- Квадратное уравнение; Квадратный трёхчлен // Энциклопедический словарь юного математика / Сост. А. П. Савин. — М.: Педагогика, 1985. — С. 133-136. — 352 с.
Ссылки
| Квадратное уравнение в Викиучебнике | |
| Квадратное уравнение на Викискладе |
- Weisstein, Eric W. Quadratic Equation (англ.) на сайте Wolfram MathWorld.
- Вывод формулы корней полного квадратного уравнения. Решение приведённых квадратных уравнений и уравнений с чётным вторым коэффициентом / Фестиваль педагогических идей «Открытый урок».
- Калькулятор квадратного уравнения.
Для улучшения этой статьи по математике желательно: |
Данная страница на сайте WikiSort.ru содержит текст со страницы сайта "Википедия".
Если Вы хотите её отредактировать, то можете сделать это на странице редактирования в Википедии.
Если сделанные Вами правки не будут кем-нибудь удалены, то через несколько дней они появятся на сайте WikiSort.ru .





















































































































































































