WikiSort.ru - Не сортированное

Каирская пятиугольная мозаика
Тип	Двойственная полуправильная мозаика[en]
Грани	неправильные пятиугольники
Диаграммы Коксетера — Дынкина
Симметрия	p4g[en]*, [4+,4], (4*2) p4, [4,4]+, (442)
Симметрия вращения	p4[en]*, [4,4]+, (442)
Двойственная мозаика	плосконосая квадратная мозаика
Конфигурация грани	V3.3.4.3.4 |
Свойства	транзитивная по граням

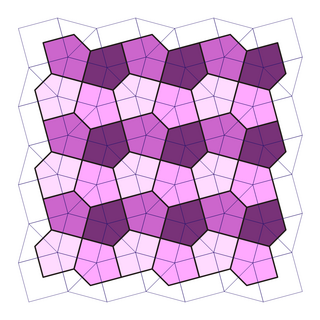
Каирская пятиугольная мозаика является двойственной полуправильной мозаикой на плоскости. Мозаика получила такое название по египетскому городу Каир, улицы которого вымощены такими плитками^[1][2]. Мозаика является одной из 15 известных равногранных (то есть имеющих грани только одного вида) пятиугольных мозаик.

Мозаика также называется сетью Макмагона^[3] по имени Перси Александра Макмагона^[en], опубликовавшего в 1921 году статью «New Mathematical Pastimes» (Новые математические развлечения)^[4].

Конвей называет мозаику 4-fold pentille (4-кратный пятипаркет)^[5].

Как 2-мерная кристаллическая решётка мозаика имеет те же специальные свойства, что и шестиугольная решётка. Обе решётки являются стандартной реализацией (в терминах М. Котани и Т. Сунада^[en]) для кристаллических решёток общего вида^[6][7].

Геометрия

Грани мозаики не являются правильными пятиугольниками — их стороны не равны (они имеют четыре длинные и одну короткую стороны с отношением ${\displaystyle 1:{\sqrt {3}}-1}$ ^[8]), а углы пятиугольника составляют (последовательно) ${\displaystyle 120^{\circ },120^{\circ },90^{\circ },120^{\circ },90^{\circ }}$ . Мозаика имеет конфигурацию грани V3.3.4.3.4.

Мозаика похожа на призматическую пятиугольную мозаику^[en] с конфигурацией грани V3.3.3.4.4, но в этой мозаике два прямых угла находятся рядом.

Вариации

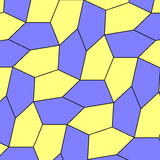
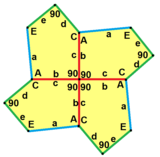
Каирская пятиугольная мозаика имеет два вида с пониженной симметрией, которые являются равногранными пятиугольными мозаиками типов 4 и 8:

p4 (442)	pgg (22×)
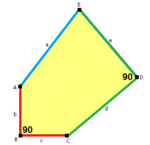b=c, d=e B=D=90°	b=c=d=e 2B+C=D+2E=360°

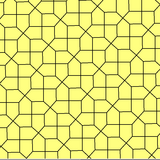
Двойственная мозаика

Мозаика является двойственной для плосконосой квадратной мозаики, состоящей из двух квадратов и трёх равносторонних треугольников вокруг каждой вершины^[9].

Связь с шестиугольными мозаиками

Эту мозаику можно рассматривать как объединение двух перпендикулярных шестиугольных мозаик, растянутых в ${\displaystyle {\sqrt {3}}}$ раз. Каждый Шестиугольник делится на четыре пятиугольника. Шестиугольники можно сделать вогнутыми, что приведёт к вогнутым пятиугольникам^[10]. Альтернативно, одну шестиугольную мозаику можно оставить правильной, а другую сжать и растянуть (в разных направлениях) в ${\displaystyle {\sqrt {3}}}$ раз, что приводит к образованию 2 видов пятиугольников.

Топологически эквивалентные мозаики

Как двойственная плосконосой квадратной мозаике данная мозаика имеет фиксированные пропорции. Однако её можно подстроить под другие геометрические формы с той же топологической связностью и другой симметрией. Например, эти мозаики топологически идентичны.

Переплетение «рогожка»[en]		Наложение на каирскую мозаику

Усечённая каирская пятиугольная мозаика

Усечение 4-валентных вершин создаёт мозаику, связанную с многогранником Голдберга^[en], и ей может быть дан символ {4+,4}_2,1. Пятиугольники усекаются до семиугольников. Двойственная мозаика к {4,4+}_2,1 имеет только треугольные грани и связана с геодезическим многогранником^[en]. Её можно рассматривать как плосконосую квадратную мозаику, в которой квадраты заменены четырьмя треугольниками.

Усечённая каирская пятиугольная мозаика

Кис-плосконосая квадратная мозаика

Связанные многогранники и мозаики

Каирская пятиугольная мозаика подобна призматической пятиугольной мозаике^[en] с конфигурацией граней V3.3.3.4.4, двум 2-однородным двойственным мозаикам и двум 3-однородным двойственным, в которых смешаны два типа пятиугольников. Здесь они нарисованы с выделением цветом рёбер^[11].

V3.3.3.4.4

V3.3.4.3.4

Связанные пятиугольные мозаики
Каирская пятиугольная мозаика		2-однородные двойственные
p4g (4*2)		p2, (2222)	pgg (22×)	cmm (2*22)
V3.3.4.3.4		(V3.3.3.4.4; V3.3.4.3.4)
Призматическая пятиугольная мозаика		3-однородные двойственные
cmm (2*22)		p2 (2222)	pgg (22×)	p2 (2222)	pgg (22×)
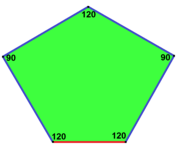V3.3.3.4.4		(V3.3.3.4.4; V3.3.4.3.4)

Каирская пятиугольная мозаика находится в последовательности двойственных плосконосых многогранников и мозаик с конфигурацией граней V3.3.4.3.n.

4n2 симметрии плосконосых мозаик: 3.3.4.3.n
Симметрия 4n2	Сферическая		Евклидова	Компактная гиперболическая				Paracomp.
	242	342	442	542	642	742	842	∞42
Плосконосые мозаики
Конфиг.	3.3.4.3.2	3.3.4.3.3	3.3.4.3.4	3.3.4.3.5	3.3.4.3.6	3.3.4.3.7	3.3.4.3.8	3.3.4.3.∞
Гиро- мозаики
Конфиг.	V3.3.4.3.2	V3.3.4.3.3	V3.3.4.3.4	V3.3.4.3.5	V3.3.4.3.6	V3.3.4.3.7	V3.3.4.3.8	V3.3.4.3.∞

Она также находится в последовательности двойственных плосконосых многогранников и мозаик с конфигурацией граней V3.3.n.3.n.

Варианты симметрии 4n2 плосконосых мозаик: 3.3.n.3.n
Симметрия 4n2	Сферияеские		Евклидовы	Компактные гиперболические				Паракомпактные
	222	322	442	552	662	772	882	∞∞2
Тела с отсечёнными вершинами
Конфиг.	3.3.2.3.2	3.3.3.3.3	3.3.4.3.4	3.3.5.3.5	3.3.6.3.6	3.3.7.3.7	3.3.8.3.8	3.3.∞.3.∞
Повёрнытые тела
Конфиг.	V3.3.2.3.2	V3.3.3.3.3	V3.3.4.3.4	V3.3.5.3.5	V3.3.6.3.6	V3.3.7.3.7	V3.3.8.3.8	V3.3.∞.3.∞

См. также

• Мозаики из выпуклых правильных многоугольников на евклидовой плоскости
• Список однородных мозаик^[en]

Примечания

Литература

• Claudi Alsina, Roger B. Nelsen. Charming proofs: a journey into elegant mathematics. — Mathematical Association of America, 2010. — Т. 42. — (Dolciani mathematical expositions). — ISBN 978-0-88385-348-1.
• George Edward Martin. Transformation Geometry: An Introduction to Symmetry. — Springer, 1982. — С. 119. — (Undergraduate Texts in Mathematics). — ISBN 978-0-387-90636-2.
• O'Keeffe M., Hyde B. G. Plane nets in crystal chemistry // Philosophical Transactions of the Royal Society of London. Series A, Mathematical and Physical Sciences. — 1980. — Т. 295. — DOI:10.1098/rsta.1980.0150.
• Major P. A. Macmahon. New Mathematical Pastimes. — University Press, 1921.
• John H. Conway, Heidi Burgiel, Chaim Goodman-Strass. Chapter 21, Naming Archimedean and Catalan polyhedra and tilings, p288 table // The Symmetries of Things. — 2008. — ISBN 978-1-56881-220-5. Архивировано 19 сентября 2010 года.
• Chavey D. Tilings by Regular Polygons—II: A Catalog of Tilings // Computers & Mathematics with Applications. — 1989. — Т. 17. — DOI:10.1016/0898-1221(89)90156-9.
• Kotani M., Sunada T. Standard realizations of crystal lattices via harmonic maps // Transactions of the American Mathematical Society. — 2000. — Т. 353.
• Sunada T. Topological Crystallography: With a View Towards Discrete Geometric Analysis. — Japan: Springer, 2012. — Т. 6. — (Surveys and Tutorials in the Applied Mathematical Sciences). — ISBN 9784431541769.

Литература для дальнейшего чтения

• Branko Grünbaum, G. C. Shephard. Tilings and Patterns. — W. H. Freeman, 1987. — С. 58—65, 480 (Chapter 2.1: Regular and uniform tilings) (Tilings by polygons, #24 of 24 polygonal isohedral types by pentagons). — ISBN 0-7167-1193-1.
• Williams, R. The Geometrical Foundation of Natural Structure: A Source Book of Design. — New York: Dover Publications, 1979. — С. 38. — ISBN 0-486-23729-X.
• David Wells. The Penguin Dictionary of Curious and Interesting Geometry. — London: Penguin, 1991. — С. 23. — ISBN 0140261494.
• Keith Critchlow. Order in Space: A design source book. — New York: Thames & Hudson, 1987. — С. 77—76, pattern 3. — ISBN 0-500-34033-1.

Ссылки

• Weisstein, Eric W. Cairo Tessellation (англ.) на сайте Wolfram MathWorld.

Для улучшения этой статьи желательно: Проверить качество перевода с иностранного языка. Исправить статью согласно стилистическим правилам Википедии.