WikiSort.ru - Не сортированное

ПОИСК ПО САЙТУ | о проекте

В Геометрии замощение — это разбиение плоскости (или другой геометрической структуры) на замкнутые множества (называемые плитками) без промежутков и наложений (отличных от границ плиток)[1]. Замощение считается периодическим, если существуют параллельные переносы в двух независимых направлениях, которые переносят плитки в точно такие же. Такое замощение состоит из одной фундаментальной единицы или примитивной ячейки, которые повторяются бесконечно в двух независимых направлениях[2]. Пример такого замощения показан на иллюстрации справа. Замощения, которые нельзя построить из единственной примитивной ячейки, называются непериодичными. Если данный набор плиток позволяет только непериодичное замощение, такой набор называется непериодичным[en] [3] Замощения, полученные из непериодичных наборов плиток, часто называют непериодичными мозаиками[en], хотя, строго говоря, следует говорить о непериодичных плитках.

Первая таблица объясняет сокращения, используемые во второй таблице. Вторая таблица содержит все известные непериодичные наборы плиток и даёт некоторую дополнительную базовую информацию о каждом наборе. Этот список плиток остаётся неполным.

Объяснения

СокращениеЗначениеОбъяснение
E2Евклидова плоскостьобычная плоскость
H2Гиперболическая
плоскость[en]		плоскость, где не выполняется аксиома параллельности
E3Евклидово
трёхмерное
пространство		пространство, определённое тремя перпендикулярными осями координат
ЛВПЛокально взаимно производныеговорят, что две плитки локально взаимно производные друг из друга, если одна плитка получается из другой простым локальным правилом (таким как удаление или вставка ребра)

Список

РисунокНазваниеЧисло плитокПростран-
ство		Дата публикацииСсылкиКомментарии
Плитки «Трилобит» и «Крест»2E21999[4]ЛВП с плитками «Стул» (квадрат с вырезанной четвертинкой)
Плитки Пенроуза P16E21974[Note 1][5]ЛВП с плитками P2 и P3, треугольниками Робинсона и плитками «звезда, лодка, шестиугольник»
Плитки Пенроуза P22E21977[Note 2][6]ЛВП с плитками P1 и P3, треугольниками Робинсона и плитками «звезда, лодка, шестиугольник»
Плитки Пенроуза P32E21978[Note 3][7]ЛВП с плитками P1 и P2, треугольниками Робинсона и плитками «звезда, лодка, шестиугольник»
Двойные плитки2E21988[8]

[9]

 Хотя плитки похожи на плитки из P3, плитки не являются ЛВП друг из друга. Мозаика разработана в попытках смоделировать расположение атомов в двойных сплавах
Плитки Робинсона[en]6E21971[Note 4][10]Плитки обеспечивают непериодичность путём образования бесконечной иерархии квадратных решёток
Нет рисункаПлитки Амманна A16E21977[11][12]Плитки обеспечивают непериодичность путём образования бесконечного иерархического двоичного дерева.
Плитки Амманна A22E21986[Note 5][13]
Плитки Амманна A33E21986[Note 5][13]
Плитки Амманна A42E21986[Note 5][13][14]ЛВП с плитками Амманна A5.
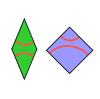Плитки Амманна A52E21982[Note 6][15]

[16]

 ЛВП с плитками Амманна A4.
Нет рисункаПлитки Пенроуза «Шестиугольник, Треугольник»2E21997[17][17][18]
Нет рисункаПлитки «Золотой треугольник»[19]10E22001[20][21]Дата соответствует времени открытия правил соединения. Двойственные плиткам Амманна A2
Плитки Соколара3E21989[Note 7][22][23]ЛВП с плитками «Щит»
Плитки «Щит»4E21988[Note 8][24][25]ЛВП с плитками Соколара
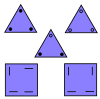Плитки «Квадрат, Треугольник»5E21986[26][27]
Мозаика «Сфинкс»91E2[28]
Плитки «Звезда, лодка, шестиугольник»3E2[29][30][31]ЛВП с плитками Пенроуза P1, P2, P3 и треугольниками Робинсона
Треугольник Робинсона4E2[12]Плитки ЛВП с плитками Пенроуза P1, P2, P3 и «Звезда, лодка, шестиугольник».
Треугольники Данцера6E21996[32][33]
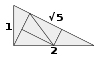Плитки «Вертушка»E21994[34][35][36][37]Дата соответствует публикации правил соединения.
Плитка Соколара-Тейлора[en]1E22010[38][39]Несвязная плитка. Непериодичная иерархическая мозаика.
Нет рисункаПлитки Вана20426E21966[40]
Нет рисункаПлитки Вана104E22008[41]
Нет рисункаПлитки Вана52E21971[Note 4][42]Плитки обеспечивают непериодичность путём образования бесконечной иерархии квадратных решёток
Плитки Вана32E21986[43]локально производные из плиток Пенроуза.
Нет рисункаПлитки Вана24E21986[43]локально производные из плиток A2
Плитки Вана16E21986[44]

[45]

 Производные из плиток A2 и их полос Амманна
Плитки Вана14E21996[46][47]
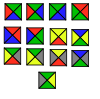Плитки Вана13E21996[48][49]
Нет рисункаПлитка «Десятиугольная губка»1E22002[50][51]Пористая плитка, состоящая из непересекающихся множеств точек
Нет рисункаСтрого непериодичные плитки Гудмана—Страусса85H22005[52]
Нет рисункаСтрого непериодичные плитки Гудмана—Страусса26H22005[53]
Гиперболическая плитка Бороцки (Böröczky)1Hn1974[54][55][56]Лишь слабо непериодична
Нет рисункаПлитка Шмитта1E31988[57]периодична по винту[en]
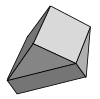Плитка Шмитта-Конвея-Данцера1E3[57]периодична по винту[en] и выпукла
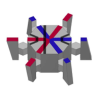Плитка Соколара-Тейлора[en]1E32010[38][39]Периодична в третьем измерении
Нет рисункаРомбоэдр Пенроуза2E31981[58][59][60][61][62][63][64][65]
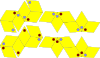Ромбоэдры Макея-Амманна4E31981[66]Обладают икосаэдральной симметрией[en]. Это декорированные ромбоэдры Пенроуза с правилами соединения, обеспечивающими непериодичность.
Нет рисункаКубики Вана21E31996[67]
Нет рисункаКубики Вана18E31999[68]
Нет рисункаТетраэдры Данцера4E31989[69][70]
Плитки I и L2En
для всех
n ≥ 3		1999[71]

Примечания

Впервые опубликовано в

1.^ Penrose, R. (1974), "The role of Aesthetics in Pure and Applied Mathematical Research", Bull. Inst. Math. and its Appl. 10: 266-271
2.^ Gardner, M. (January 1977), "Extraordinary nonperiodic tiling that enriches the theory of tiles", Scientific American 236: 110-121
3.^ Penrose, R. (1978), "Pentaplexity", Eureka 39: 16-22
4.^ Robinson, R. (1971), "Undecidability and nonperiodicity of tilings in the plane", Inv. Math. 12: 177-209
5.^ Grünbaum, Shephard, 1986.
6.^ Beenker, F. P. M.(1982), "Algebraic theory of non-periodic tilings of the plane by two simple building blocks: a square and a rhombus", Eindhoven University of Technology, TH Report 82-WSK04
7.^ Socolar, J. E. S. (1989), "Simple octagonal and dodecagonal quasicrystals", Phys. Rev. A 39: 10519-51
8.^ Gähler, F., "Crystallography of dodecagonal quasicrystals", published in Janot, C.: Quasicrystalline materials : Proceedings of the I.L.L. / Codest Workshop, Grenoble, 21–25 March 1988. Singapore : World Scientific, 1988, 272-284
  1. ↑ Tilings by Regular Polygons // Math. Mag.. — 1977. — Т. 50, вып. 5. — С. 227–247. — DOI:10.2307/2689529.(архив WebCite)
  2. ↑ Edwards S., Fundamental Regions and Primitive cells (архив WebCite)
  3. ↑ Stan Wagon. Mathematica in action. — 2nd. — New York, Berlin, Heidelberg: Springer Verlag, 1998. — С. 216 (9.1 NonPeriodic Tilings). — ISBN 0-387-98252-3.
  4. ↑ A Small Aperiodic Set of Planar Tiles // European Journal of Combinatorics. — 1999. — Т. 20, вып. 5. — С. 375–384. — DOI:10.1006/eujc.1998.0281. (доступен препринт here)
  5. ↑ Mikhael J. Colloidal Monolayers On Quasiperiodic Laser Fields (см. страницу 23) (архив WebCite)
  6. ↑ Gardner M. Penrose tiles to trapdoor ciphers (см. страницу 86) (архив WebCite)
  7. ↑ Pentaplexity // Math. Intell.. — 1979/80. — Т. 2. — С. 32–37. — DOI:10.1007/bf03024384.(архив WebCite)
  8. ↑ Two-dimensional system with a quasi-crystalline ground state // J. Phys. France. — 1988. — Т. 49, вып. 2. — С. 249–256. — DOI:10.1051/jphys:01988004902024900. (архив WebCite)
  9. ↑ A simple example of a non-Pisot tiling with five-fold symmetry // J. Phys. I France. — 1992. — Т. 2, вып. 2. — С. 207–220. — DOI:10.1051/jp1:1992134.(архив WebCite)
  10. ↑ Aperiodic Hierarchical tilings // Proc. of NATO-ASI "Foams, Emulsions, and Cellular Materials" Ser. E. — 1999. — Т. 354. — С. 481–496. — DOI:10.1007/978-94-015-9157-7_28.
  11. ↑ The Colossal Book of Mathematics. — W. W. Norton & Company, 2001. — С. 76.
  12. 1 2 Grünbaum, Shephard, 1986, согласно ;
  13. 1 2 3 Aperiodic Tiles // Discrete Comp Geom. — 1992. — Т. 8. — С. 1–25. — DOI:10.1007/BF02293033.
  14. ↑ Harris E., Frettlöh D. Ammann A4
  15. ↑ Representation of Ammann-Beenker tilings by an automaton // Nihonkai Math. J.. — 2004. — Т. 15. — С. 109–118. (архив WebCite)
  16. ↑ Harris E., Frettlöh D. Ammann-Beenker
  17. 1 2 R. Penrose. The Mathematics of Long-Range Aperiodic Order / Moody R.V.. — Nato Asi Series C. — Dordrecht: Kluwer, 1997. — Т. 489. — С. 467–497. — ISBN 978-0-7923-4506-0. — DOI:10.1007/978-94-015-8784-6_18. R. Penrose. The Mathematics of Long-Range Aperiodic Order / Moody R.V.. — Springer Verlag GMBH, 2010. — Т. 489. — С. 467–497. — (Nato Asi Series U). — ISBN 9048148324. — DOI:10.1007/978-94-015-8784-6_18.
  18. ↑ C. Goodman-Strauss, An aperiodic pair of tiles
  19. ↑ Плитка не соответствует равнобедренному «Золотому треугольнику» и является прямоугольным треугольником с золотым соотношением гипотенузы к катету
  20. ↑ A species of planar triangular tilings with inflation factor  // Res. Bull. Panjab Univ. Sci.. — 2001. — Т. 50, вып. 1-4. — С. 137–175.
  21. ↑ Fractal Penrose tiles II. Tiles with fractal boundary as duals of Penrose triangles // Aequationes Math.. — 1997. — Т. 54. — С. 108–116. — DOI:10.1007/bf02755450.
  22. ↑ Dodecagonal tilings as maximal cluster coverings. Проверено 25 сентября 2013.
  23. ↑ The Socolar tiling
  24. ↑ Gähler F., Frettlöh D. Shield
  25. ↑ Matching rules for quasicrystals: the composition-decomposition method // J. of Non-crystalline Solids. — 1993. — Т. 153&154. — С. 160–164. — DOI:10.1016/0022-3093(93)90335-u.(архив WebCite)
  26. ↑ A Dodecagonal Quasiperiodic Lattice in Two Dimensions // Helv. Phys. Acta.. — 1986. — Т. 59. — С. 1260–1263.
  27. ↑ Hermisson J., Richard C., Baake M. A Guide to the Symmetry Structure of Quasiperiodic Tiling Classes (архив WebCite)
  28. ↑ Goodman-Strauss C., Aperiodic tilings (см. страницу 74)
  29. ↑ Quasicrystals and Penrose patterns // Current Science. — 1991. — Т. 61. — С. 315.
  30. ↑ A two dimensional aperiodic dense tiling // J. Phys. France. — 1989. — Т. 50. — С. 19–33. — DOI:10.1051/jphys:0198900500101900. (архив WebCite)
  31. ↑ Combined energy-diffraction data refinement of decagonal AlNiCo // J. Non-Cryst. Solids. — 2004. — Т. 334&335. — С. 177–183. (архив WebCite)
  32. ↑ Nischke, K-P and Danzer, L,. A construction of inflation rules based on $n$-fold symmetry // Discrete Comput. Geom.. — 1996. — Т. 15, вып. 2. — С. 221–236. — DOI:10.1007/bf02717732. 96j:52035
  33. ↑ Hayashi H., Kawachi Y., Komatsu K., Konda A., Kurozoe M., Nakano F., Odawara N., Onda R., Sugio A., Yamauchi M. Abstract:Notes on vertex atlas of planar Danzer tiling
  34. ↑ The pinwheel tilings of the plane // Annals of Mathematics. Second Series. — 1994. — Т. 139, вып. 3. — С. 661–702. — DOI:10.2307/2118575.
  35. ↑ Symmetry Of Tilings Of The Plane // Annals of Mathematics. — 1994. — DOI:10.1090/s0273-0979-1993-00425-7.
  36. ↑ Space tilings and local isomorphism // Geom. Dedicata. — 1992. — Т. 42, вып. 3. — С. 355–360. — DOI:10.1007/bf02414073.
  37. ↑ The mathematics of long-range aperiodic order. — Kluwer Acad. Publ., Dordrecht, 1997.
  38. 1 2 Socolar J. E. S. and Taylor J. M. An aperiodic hexagonal tile
  39. 1 2 Socolar J. E. S. and Taylor J. M. Forcing nonperiodicity with a single tile
  40. ↑ The Undecidability of the Domino Problem // Memoirs of the American Mathematical Society. — 1966. — Т. 66. — С. 1–72.
  41. ↑ Two-by-two Substitution Systems and the Undecidability of the Domino Problem. — Springer, 2008. — С. 476–485.
  42. ↑ Deterministic Aperiodic Tile Sets // Geometric and Functional Analysis. — 1999. — Т. 9. — С. 353–369. — DOI:10.1007/s000390050090.
  43. 1 2 Aperiodic Sets of Square Tiles with Colored Corners // Report CW. — 2006. — Т. 460. — С. 12. Архивировано 2 октября 2010 года.
  44. ↑ Grünbaum, Shephard, 1986.
  45. ↑ A. Carbone, M. Gromov, P. Prusinkiewicz. Pattern Formation in Biology, Vision and Dynamics. — Singapore: World Scientific Publishing Co. Pte. Ltd., 2000. — ISBN 981-02-3792-8.
  46. ↑ Kari J. A small aperiodic set of Wang tiles". Discrete Mathematics, 160(1-3):259-264
  47. ↑ Lagae A. Tile Based Methods in Computer Graphics Dissertation (см. страницу 149) (архив WebCite)
  48. ↑ Culik K., Kari J. On aperiodic sets of Wang tiles
  49. ↑ K. Culik. An aperiodic set of 13 Wang tiles. Проверено 25 сентября 2013. Архивировано 2 октября 2010 года.
  50. ↑ Zhu F. The Search for a Universal Tile
  51. ↑ D. A. Bailey, F. Zhu. A Sponge-Like (Almost) Universal Tile. Проверено 25 сентября 2013.
  52. ↑ Goodman-Strauss C., A hierarchical strongly aperiodic set of tiles in the hyperbolic plane
  53. ↑ A strongly aperiodic set of tiles in the hyperbolic plane // Invent. Math.. — 2005. — Т. 159. — С. 130–132. — DOI:10.1007/s00222-004-0384-1. — Bibcode: 2004InMat.159..119G.
  54. ↑ Gömbkitöltések állandó görbületü terekben I // Mat. Lapok.. — 1974. — Т. 25. — С. 265–306.Gömbkitöltések állandó görbületü terekben II // Mat. Lapok.. — 1974. — Т. 26. — С. 67–90.
  55. ↑ A strongly aperiodic set of tiles in the hyperbolic plane // Invent. Math.. — 2005. — Т. 159. — С. 120. — DOI:10.1007/s00222-004-0384-1. — Bibcode: 2004InMat.159..119G.
  56. ↑ Dolbilin N., Frettlöh D. Properties of Böröczky tilings in high dimensional hyperbolic spaces (архив WebCite)
  57. 1 2 Aperiodic tilings in higher dimensions // Proceedings of the American Mathematical Society. — American Mathematical Society, 1995. — Т. 123, вып. 11. — С. 3543–3548. — DOI:10.2307/2161105.
  58. ↑ Маккей Аллан. JI. DE NTVE QUINQUANGULA о пятиугольных снежинках // Кристаллография. — 1981. — Т. 26, вып. 5. — С. 910-919.. (архив WebCite)
  59. ↑ Meisterernst G. Experimente zur Wachstumskinetik Dekagonaler Quasikristalle (Experiments on the growth kinetics of decagonal quasicrystals) Dissertation (см. страницу 18-19) (архив WebCite)
  60. ↑ Structure Transition of the Three-Dimensional Penrose Tiling Under Phason Strain Field // Chinese Phys. Lett.. — 1993. — Т. 10, No.8. — С. 449–452. — DOI:10.1088/0256-307x/10/8/001. (архив WebCite)
  61. ↑ Inchbald G. A 3-D Quasicrystal Structure
  62. ↑ Quasicrystals: tiling versus clustering // Phil. Mag. A. — 2001. — Т. 81. — С. 2645–2651. — DOI:10.1080/01418610108216660. (архив WebCite)
  63. ↑ Rudhart C. P. Zur numerischen Simulation des Bruchs von Quasikristallen (On the numeric simulation of cracking in quasicrystals) см. страницу 11
  64. ↑ Tilings, coverings, clusters and quasicrystals // Current Science. — 2000. — Т. 78, вып. 1. — С. 64–72. (архив WebCite)
  65. ↑ Theory of Matching Rules for the 3-Dimensional Penrose Tilings // Commun. Math. Phys.. — 1988. — Т. 118, вып. 2. — С. 263–288. — DOI:10.1007/BF01218580. (архив WebCite)
  66. ↑ Eric A. Lord. Quasicrystals and Penrose patterns // Current Science. — 1991. — Т. 61, вып. 5. — С. 313.
  67. ↑ K. Culik, J. Kari. An aperiodic set of Wang cubes. Проверено 25 сентября 2013.
  68. ↑ G. Walther, C. Selter. Mathematikdidaktik als design science. — Leipzig: Ernst Klett Grundschulverlag, 1999. — ISBN 3122000601.
  69. ↑ L. Danzer. Three-Dimensional Analogs of the Planar Penrose Tilings and Quasicrystals // Discrete Mathematics. — 1989. — Т. 76. — С. 1–7. — DOI:10.1016/0012-365X(89)90282-3.
  70. ↑ Zerhusen A., Danzer’s three dimensional tiling
  71. ↑ An Aperiodic Pair of Tiles in En for all n ≥ 3 // European Journal of Combinatorics. — 1999. — Т. 20, вып. 5. — С. 385–395. — DOI:10.1006/eujc.1998.0282. (доступен препринт here)

Литература

  • B. Grünbaum, G. C. Shephard. Tilings and Patterns. — New York: W.H. Freeman and Company, 1986. — ISBN 0-7167-1193-1.

Ссылки

Данная страница на сайте WikiSort.ru содержит текст со страницы сайта "Википедия".

Если Вы хотите её отредактировать, то можете сделать это на странице редактирования в Википедии.

Если сделанные Вами правки не будут кем-нибудь удалены, то через несколько дней они появятся на сайте WikiSort.ru .



Текст в блоке "Читать" взят с сайта "Википедия" и доступен по лицензии Creative Commons Attribution-ShareAlike; в отдельных случаях могут действовать дополнительные условия.

Другой контент может иметь иную лицензию. Перед использованием материалов сайта WikiSort.ru внимательно изучите правила лицензирования конкретных элементов наполнения сайта.

2019-2025
WikiSort.ru - проект по пересортировке и дополнению контента Википедии