WikiSort.ru - Не сортированное

Случайное блуждание — математическая модель процесса случайных изменений — шагов в дискретные моменты времени. При этом предполагается, что изменение на каждом шаге не зависит от предыдущих и от времени. В силу простоты анализа эта модель часто используется в разных сферах в математике, экономике, физике, но, как правило, такая модель является существенным упрощением реального процесса.

Одномерное дискретное случайное блуждание

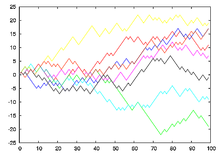
Одномерное дискретное случайное блуждание — это случайный процесс ${\displaystyle \{Y_{n}\}_{n\geqslant 0}}$ с дискретным временем, имеющий вид

${\displaystyle Y_{n}=Y_{0}+\sum \limits _{i=1}^{n}X_{i}}$ ,

где

• ${\displaystyle Y_{0}}$  — начальное состояние;
• ${\displaystyle X_{i}={\begin{cases}1,&p_{i}\\-1,&q_{i}\equiv 1-p_{i}\end{cases}},\quad 0<p_{i}<1,\quad i\in \mathbb {N} }$ ;
• случайные величины ${\displaystyle Y_{0},X_{i},i=1,2,\ldots }$ совместно независимы.

Общее определение

Пусть ${\displaystyle (X_{1},X_{2},\dotsc )}$ последовательность независимых случайных величин со значениями в ${\displaystyle \mathbb {R} ^{d}}$ и одинаковыми распределениями. Тогда случайный процесс заданный последовательностью

${\displaystyle Y_{n}=Y_{0}+\sum _{j=1}^{n}X_{j},\qquad n\in \mathbb {N} _{0}}$

называется случайным блужданием в ${\displaystyle \mathbb {R} ^{d}}$ или d-мерным случайным блужданием.^[1] Случайное блуждание это дискретный случайный процесс с независимыми стационарными приращениями.

Теорема Донскера

Рассмотрим случайное блуждание ${\displaystyle Y_{n}=\sum \limits _{i=1}^{n}{X_{i}}}$ , где ${\displaystyle EX_{i}=0,DX_{i}=\sigma ^{2}<\infty }$ .

Центральная предельная теорема утверждает, что ${\displaystyle {\frac {Y_{n}}{\sigma {\sqrt {n}}}}\rightarrow N(0,1)}$ по распределению при ${\displaystyle n\rightarrow \infty }$ .

Однако, в случае случайных блужданий, это утверждение можно значительно усилить.

Построим по ${\displaystyle Y_{n}}$ случайный процесс ${\displaystyle S_{n}(t),t\in [0,1]}$ , определив его следующим образом: ${\displaystyle S_{n}\left({\frac {k}{n}}\right)={\frac {Y_{k}}{\sigma {\sqrt {n}}}}}$ , а при остальных ${\displaystyle t}$ мы доопределим процесс линейным продолжением:

${\displaystyle S_{n}(t)=(k+1-nt)S_{n}\left({\frac {k}{n}}\right)+(nt-k)S_{n}\left({\frac {k+1}{n}}\right),t\in \left({\frac {k}{n}};{\frac {k+1}{n}}\right)}$

Из центральной предельной теоремы ${\displaystyle \forall t}$ ${\displaystyle S_{n}(t)\rightarrow N(0,t)}$ по распределению при ${\displaystyle n\rightarrow \infty }$

Это означает сходимость одномерных распределений процесса ${\displaystyle S_{n}(t)}$ к одномерным распределениям винеровского процесса. Теорема Донскера, называемая также принципом инвариантности, утверждает, что имеет место слабая сходимость процессов, ${\displaystyle S_{n}(t)\rightarrow W(t),n\rightarrow \infty }$

Слабая сходимость процессов означает сходимость непрерывных по винеровской мере функционалов, то есть позволяет рассчитывать значения функционалов от броуновского движения (например максимума, минимума, последнего нуля, момента первого достижения уровня и других) предельным переходом от простого случайного блуждания.

Применения

• С использованием случайных блужданий возможна организация траектории движения в пространстве параметров оптимизируемой целевой функции, что применяется при решении задач оптимизации^[2]. При использовании специального закона распределения случайных величин может быть получена модификация метода случайных блужданий, именуемая полетами Леви (англ.).
• С помощью случайных блужданий можно решить краевую задачу для уравнений Максвелла в интегральной форме. Интеграл считается с помощью метода Монте-Карло, при этом подинтегральная функция семплируется с помощью случайного блуждания. Таким образом можно найти взаимные емкости проводников в интегральных схемах, обходя требования методов конечных и граничных элементов к дискретизации пространства, что играет определяющую роль в выборе метода с учетом увеличения количества вентилей в современных интегральных схемах. В отличие от методов конечных и граничных элементов, метод случаных блужданий находит сразу интеграл от поля, а не поле в каждой точке, которое потом интегрируют, находя емкость.^[3] Методы случайного блуждания стали де-факто стандартом в начале 21 века в нахождении паразитных емкостей интегральных схем.

Примечания

См. также

• Винеровский процесс
• Задача о разорении игрока
• Интегрированный временной ряд

Литература

• Скопенков, М.; Смыкалов, В.; Устинов, А. Случайные блуждания и электрические цепи (рус.) // Матем. просв., сер. 3. — 2012. — Т. 16. — С. 25—47.