В геометрии построение Витхоффа, или конструкция Витхоффа[1] — это метод построения однородных многогранников[en] или мозаик на плоскости. Метод назван по имени математика В. А. Витхоффа[en]. Часто метод построения Витхоффа называют калейдоскопным построением.
Построение
Построение основано на идее мозаик на сфере с использованием сферических треугольников — см. треугольники Шварца. Это построение использует отражения относительно сторон треугольника подобно калейдоскопу. Однако, в отличие от калейдоскопа, отражения не параллельны, а пересекаются в одной точке. Многократные отражения образуют несколько копий треугольника. Если углы сферического треугольника выбраны правильно, треугольники покрывают сферу мозаикой один или более раз.
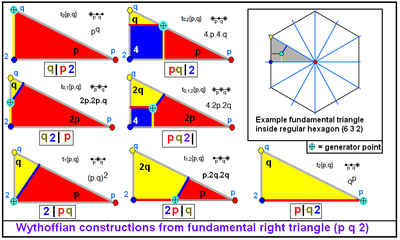
Если поместить точку в подходящее место внутри сферического треугольника, окружённого зеркалами, можно добиться, чтобы отражения этой точки дали однородный многогранник. Для сферического треугольника ABC имеются четыре позиции, которые дают однородный многогранник:
- Точка расположена в вершине A. Она даёт многогранник с символом Витхоффа a|b c, где a равен π, делённому на угол треугольника в вершине A. Аналогично для b и c.
- Точка расположена на отрезке AB в основании биссектрисы угла в вершине C. Она даёт многогранник с символом Витхоффа a b|c.
- Точка расположена в инцентре треугольника ABC. Она даёт многогранник с символом Витхоффа a b c|.
- Точка расположена таким образом, что при вращении её вокруг вершин треугольника на удвоенный угол при этих вершинах, она перемещается на одно и тоже расстояние. Используются только чётные отражения. Многогранник имеет символ Витхоффа |a b c.
Процесс, в общем случае, применим и для получения правильных политопов в пространствах более высоких размерностей, включая 4-мерные однородные политопы[en].
  Шестиугольная призма строится как из семейства (6 2 2), так и из семейства (3 2 2). |
  Обрезанная квадратная мозаика[en] строится с помощью двух различных позиций в семействе (4 4 2). |
Невитхоффово построение
Однородные многогранники[en], которые нельзя построить с помощью зеркального построения Витхоффа, называются невитхоффовыми. Их, в общем случае, можно получить из витхоффовых построений либо альтернацией[en] (удаление вершин через одну) или вставкой чередующихся рядов некоторых фигур. Оба типа таких фигур обладают вращательной симметрией. Иногда обрезки[en] считаются витхоффовыми, даже если они могут быть получены путём альтернации обрезанных со всех сторон фигур.
 Шестиугольная антипризма строится с помощью альтернации двенадцатиугольной призмы[en]. |
 Удлинённая треугольная мозаика[en] строится путём чередования строк квадратной мозаики и треугольной мозаики. |
 Большой биромбоикосододекаэдр[en] является единственным невитхоффовым однородным многогранником. |
См. также
- Символ Витхоффа[en] — символ для построения Витхоффа однородных многогранников[en] и однородных мозаик.
- Диаграммы Коксетера — Дынкина — обобщённый символ для построения Витхоффа однородных многогранников[en] и сот.
Примечания
Литература
- H. S. M. Coxeter. Chapter 5: The Kaleidoscope, Section: 5.7 Wythoff's construction // Regular Polytopes[en]. — Dover edition, 1973. — ISBN 0-486-61480-8.
- Coxeter. Chapter 3: Wythoff's Construction for Uniform Polytopes // The Beauty of Geometry: Twelve Essays. — Dover Publications, 1999. — ISBN 978-0-486-40919-1.
- Har'El, Z. Uniform Solution for Uniform Polyhedra // Geometriae Dedicata. — 1993. — № 47. — С. 57—110. Архивировано 15 июля 2009 года. Section 4: The Kaleidoscope.
- W.A. Wythoff[en]. A relation between the polytopes of the C600-family // Proceedings of the Section of Sciences. — Koninklijke Akademie van Wetenschappen te Amsterdam, 1918. — № 20. — С. 966—970.
- А. Ю. Веснин. Прямоугольные многогранники и трехмерные гиперболические многообразия // УМН. — 2017. — Т. 72. — С. 147–190. — DOI:10.4213/rm9762.
Ссылки
- Weisstein, Eric W. Wythoff Construction (англ.) на сайте Wolfram MathWorld.
- Olshevsky, George Wythoff construction at Glossary for Hyperspace
- Однородные многоугольники, полученные с помощью построения Витхоффа
- Описание построения Витхоффа
- "Jenn", программное обеспечение для просмотра (сферических) многоугольников и четырёхмерных политопов из их групп симметрии
Для улучшения этой статьи желательно: |
Данная страница на сайте WikiSort.ru содержит текст со страницы сайта "Википедия".
Если Вы хотите её отредактировать, то можете сделать это на странице редактирования в Википедии.
Если сделанные Вами правки не будут кем-нибудь удалены, то через несколько дней они появятся на сайте WikiSort.ru .