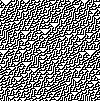
Элементарный клеточный автомат — это клеточный автомат с одномерным массивом ячеек в форме бесконечной в обе стороны ленты, который имеет два возможных состояния ячеек (0 и 1, «мёртвые» и «живые», «пустые» и «заполненные») и правило для определения состояния ячейки на следующем шаге, использующее только состояние ячейки и её двух соседей на текущем шаге. В целом такие автоматы являются одними из наиболее простых возможных клеточных автоматов, однако при некоторых правилах они показывают сложное поведение; так, выбор правила 110 приводит к полному по Тьюрингу автомату.
Код Вольфрама

Всего существует возможных комбинаций состояния ячейки и состояний её двух соседей. Правило, определяющее элементарный клеточный автомат, должно указывать следующее состояние (0 или 1) для каждого из этих возможный случаев, поэтому всего правил . Стивен Вольфрам предложил схему нумерации этих правил, известную как код Вольфрама (англ. Wolfram code), которая сопоставляет каждому правилу число от 1 до 255. Эта система была впервые опубликована Вольфрамом в статье 1983 года[1] и позднее использовалась в его книге «A New Kind of Science» (англ. Наука нового типа).[2]
Для получения кода Вольфрама нужно записать в убывающем порядке возможные конфигурации (111, 110, …, 001, 000), выписать под ними соответствующие состояния и интерпретировать получившуюся последовательность нулей и единиц как число в двоичной системе счисления. Например, следующая схема приводит к коду , соответствующему правилу 110:
| текущие состояния | 111 | 110 | 101 | 100 | 011 | 010 | 001 | 000 |
|---|---|---|---|---|---|---|---|---|
| будущее состояние | 0 | 1 | 1 | 0 | 1 | 1 | 1 | 0 |
Отражения и дополнения
Некоторые из 256 правил тривиальным образом эквивалентны друг другу благодаря наличию двух видов преобразований. Первый — это отражение относительно вертикальной оси, при котором левый и правый соседи меняются местами и получается зеркальное правило (англ. mirrored rule). Например, правило 110 становится правилом 118:
| текущие состояния | 111 | 110 | 101 | 100 | 011 | 010 | 001 | 000 |
|---|---|---|---|---|---|---|---|---|
| будущее состояние | 0 | 1 | 1 | 1 | 0 | 1 | 1 | 0 |
Среди 256 правил есть 64 зеркально-симметричных (англ. amphichiral).
Второй вид преобразований — это замена ролей 0 и 1 в определении, дающее дополнительное правило (англ. complementary rule). Например, правило 110 становится правилом 137:
| текущие состояния | 111 | 110 | 101 | 100 | 011 | 010 | 001 | 000 |
|---|---|---|---|---|---|---|---|---|
| будущее состояние | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 1 |
Всего 16 правил из 256 совпадают со своими дополнениями. С точностью до этой пары преобразований (в том числе применённой одновременно — порядок не важен), существует 88 неэквивалентных элементарных клеточных автоматов.[3]
Методы исследования
Простейшая конфигурация

Один из методов исследования элементарных клеточных автоматов — рассмотреть эволюцию простейшей начальной конфигурации, то есть состоящей всего из одной живой (содержащей 1) клетки. Если правило имеет чётный код Вольфрама, то не происходит самопроизвольного зарождения жизни (комбинация 000 не даёт посередине 1 в следующем поколении), а потому каждое состояние простейшей конфигурации имеет конечное число ненулевых ячеек и может быть проинтерпретировано как число в двоичной записи.[как?] Последовательность этих чисел задаёт производящую функцию, которая является рациональной, то есть отношением двух многочленов, и часто имеет относительно простой вид.
Случайные конфигурации
Также полезно рассмотреть эволюцию случайных начальных конфигураций. Для этого существует разделение на следующие неформальные классы клеточных автоматов, придуманное Вольфрамом:[4]
- Класс 1: Быстро сходится к состоянию из одних нулей или единиц. Вольфрам приводит как примеры правила 0, 32, 160, 232.
- Класс 2: Быстро сходится к циклическому или стабильному состоянию. Например, правила 4, 108, 218, 250.
- Класс 3: Сохраняется в случайном состоянии. Например, правила 22, 30, 126, 150, 182.
- Класс 4: Образуются как области с циклическими или стабильными состояниями, так и структуры, которые взаимодействуют друг с другом сложными способами. Примером является правило 110, являющееся полным по Тьюрингу.
Неоднозначные случаи
Некоторые правила нельзя однозначно отнести к одному из классов, например:
- 62: случайные структуры взаимодействуют сложным образом, однако склонны уничтожать друг друга; в результате, если начинать со случайной конфигурации, то первое время будет проявляться поведение, свойственное классу 4, но в конце с большой вероятностью окажется циклическое или стабильное состояние, как у автоматов класса 2.
- 73: комбинация 0110 сохраняется в следующих поколениях, что создаёт стены, блокирующие передвижение информации; это приводит к повторению комбинаций между стенами, то есть как поведению класса 2; однако запрет начальных комбинаций с блоками из чётного числа подряд идущих нулей и единиц приводит к поведению, типичному для автоматов класса 3.
- 54: класс 4, но полнота по Тьюрингу неизвестна.
Примечания
- ↑ Wolfram, Stephen (July 1983). “Statistical Mechanics of Cellular Automata”. Reviews of Modern Physics. 55: 601—644. Bibcode:1983RvMP...55..601W. DOI:10.1103/RevModPhys.55.601.
- ↑ Wolfram, Stephen, A New Kind of Science. Wolfram Media, Inc., May 14, 2002. ISBN 1-57955-008-8
- ↑ Elementary Cellular Automata. Rule properties:Equivalent rules в «Wolfram Atlas of Simple Programs»
- ↑ Stephan Wolfram, A New Kind of Science, p. 223.
Ссылки
| Элементарный клеточный автомат на Викискладе |
- Элементарные клеточные автоматы в «Wolfram Atlas of Simple Programs»
Для улучшения этой статьи желательно: |
Данная страница на сайте WikiSort.ru содержит текст со страницы сайта "Википедия".
Если Вы хотите её отредактировать, то можете сделать это на странице редактирования в Википедии.
Если сделанные Вами правки не будут кем-нибудь удалены, то через несколько дней они появятся на сайте WikiSort.ru .





