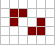
Натюрмо́рт — класс конфигураций в «Жизни» — созданной Конвеем модели клеточного автомата.
Описание
Натюрморты — конфигурации «Жизни» или другого клеточного автомата, которые не изменяются в процессе эволюции[1]. Иными словами, натюрморт является осциллятором периода 1[2][3][4].
Терминология: натюрморты и псевдонатюрморты
Существует несколько близких по смыслу терминов, обозначающих не изменяющиеся в процессе эволюции конфигурации (конфигурации, являющиеся собственными родителями). Различия между ними связаны с ответом на следующие вопросы:
- Считается ли натюрмортом конфигурация, состоящая из двух независимых натюрмтортов (например, двух блоков на достаточно большом расстоянии друг от друга)?[5]
- Считается ли натюрмортом конфигурация, состоящая из двух частей, любую из которых можно удалить так, что вторая часть останется родителем себя?
В существующих словарях и онлайн-энциклопедиях[6][7][4][8] приводятся следующие определения:
- Устойчивый образец (англ. stable pattern) — объект, который является собственным родителем[2][3];
- Натюрморт (англ. still life, strict still life) — устойчивый объект, являющийся конечным и непустым, который не может быть разделён на две устойчивые части[9][10][8];
- Псевдонатюрморт (англ. pseudo still life) — устойчивый объект, не являющийся натюрмортом, в котором присутствует хотя бы одна мёртвая клетка, имеющая более трёх соседей всего, но меньше трёх соседей в каждом из составляющих объект натюрмортов[11][12][8].
Точное определение «устойчивости» представляет интерес в контексте перечисления натюрмортов: например, согласно приведённым определениям, количество устойчивых конфигураций размера 8 (т.е. состоящих из 8 живых клеток) в «Жизни» бесконечно, так как пара блоков на любом расстоянии друг от друга является устойчивой; тем не менее, количество натюрмортов ограниченного размера считается конечным[6][7][8].
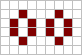 | Псевдонатюрморт в «Жизни». Удаление одного из островов не влияет на стабильность второго острова. |
 | «Строгий» натюрморт. Стабильность каждого из островов зависит от наличия другого острова. |
Известно число натюрмортов и псевдонатюрмортов размера не выше 24 клеток[11][12][8].
Задача определения типа устойчивой конфигурации (натюрморт, псевдонатюрморт) решается за полиномиальное время путём поиска циклов в связанном кососимметричном графе[13].
Натюрморты в «Жизни»
В «Жизни» существует множество естественных[14] натюрмортов.
Простые примеры
Блок
Наиболее распространённый натюрморт — блок[15][16][17] — конфигурация в форме квадрата 2 × 2. Два блока, размещённые в прямоугольнике 2 × 5, образуют би-блок — простейший псевдонатюрморт. Блоки используются в качестве составных частей во множестве сложных устройств, например, в планерном ружье Госпера[17].
Улей
Второй по распространённости натюрморт — улей (англ. hive, beehive). Ульи часто возникают четвёрками в конфигурации, называемой па́секой (англ. honey farm)[15][16][17].
 |
Каравай
Третий по распространённости натюрморт — каравай (англ. loaf). Караваи нередко появляются парами (англ. bi-loaf)[15][16][17]. В свою очередь, двойные караваи также появляются в парах, называемых пека́рнями (англ. bakery)[18].
 |
 |
Ящики, баржи, лодки, корабли
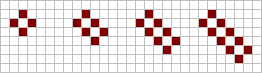
Ящик (англ. tub) состоит из четырёх живых клеток в окрестности фон Неймана центральной мёртвой клетки. Добавление одной живой клетки по диагонали к центральной клетке превращает ящик в лодку (англ. boat), а добавление симметрично ещё одной клетки — в корабль (англ. ship)[19]. Естественное удлинение этих трёх конфигураций даёт баржу (англ. barge), длинную лодку (англ. long-boat) и длинный корабль (англ. long-ship) соответственно. Удлинение можно продолжать сколь угодно долго[16][6][7][17].
 |
 |
 |
Из двух лодок можно составить ещё один натюрморт — лодочный бант (англ. boat tie), а из двух кораблей — корабельный бант (англ. ship tie)[6][7].
 |
 |
Другие натюрморты
Пожиратели и отражатели
Натюрморты можно использовать для модификации или разрушения других объектов. Пожиратель (англ. eater) способен уничтожить космический корабль и восстановиться после реакции. Отражатель (англ. reflector) вместо уничтожения космического корабля изменяет направление его полёта.
Отражатели и пожиратели не обязательно должны являться натюрмортами.
Максимальная плотность
Задача размещения в области n × n натюрморта с максимальным числом клеток привлекала к себе внимание программистов как задача программирования в ограничениях[20][21][22][23][24]. При стремлении размера области к бесконечности, живыми могут быть не более 50% клеток[25]. На конечных квадратных областях можно достичь больших плотностей. Так, максимальная плотность натюрморта в квадрате 8 × 8 равна 36/64 = 0.5625 — эту плотность обеспечивает образец, состоящий из девяти блоков[20] Для квадратов до 20 × 20 известны оптимальные решения[26][27].
Число натюрмортов
Число натюрмортов и псевдонатюрмортов в «Жизни» известно до размера в 24 клетки[28][29][30].
| Число живых клеток | Число натюрмортов | Примеры |
|---|---|---|
| 1 | 0 | |
| 2 | 0 | |
| 3 | 0 | |
| 4 | 2 | блок, ящик |
| 5 | 1 | лодка |
| 6 | 5 | баржа, авианосец, улей, корабль, змея |
| 7 | 4 | рыболовный крючок, каравай, длинная лодка |
| 8 | 9 | каноэ, манго, длинная баржа, пруд |
| 9 | 10 | знак интеграла |
| 10 | 25 | лодочный бант |
| 11 | 46 | |
| 12 | 121 | корабельный бант |
| 13 | 240 | |
| 14 | 619 | двойной каравай |
| 15 | 1353 | |
| 16 | 3286 | |
| 17 | 7773 | |
| 18 | 19044 | |
| 19 | 45759 | пожиратель 2 |
| 20 | 112243 | |
| 21 | 273188 | |
| 22 | 672172 | |
| 23 | 1646147 | |
| 24 | 4051711 |
Примечания
- ↑ Более строгие определения см. в разделе «Терминология».
- 1 2 Устойчивый. Словарь Жизни.
- 1 2 Stable (недоступная ссылка). Life Lexicon. Проверено 11 августа 2013. Архивировано 20 февраля 2009 года.
- 1 2 Eric Weisstein. Still Life. Treasure Trove of Life C.A.. Проверено 11 августа 2013.
- ↑ Если ответ на этот вопрос положительный, то количество натюрмортов с ограниченным числом клеток бесконечно.
- 1 2 3 4 Николай Белюченко. Словарь Жизни. Архивировано 10 октября 2012 года.
- 1 2 3 4 Stephen A. Silver. Life Lexicon (англ.). Архивировано 26 мая 2013 года.
- 1 2 3 4 5 Still life. ConwayLife.com. Проверено 11 августа 2013.
- ↑ Натюрморт. Словарь Жизни.
- ↑ Still life (недоступная ссылка). Life Lexicon. Проверено 11 августа 2013. Архивировано 20 февраля 2009 года.
- 1 2 Псевдонатюрморт. Словарь Жизни.
- 1 2 Pseudo still life (недоступная ссылка). Life Lexicon. Проверено 11 августа 2013. Архивировано 3 декабря 2014 года.
- ↑ Cook, Matthew (2003). "Still life theory". New Constructions in Cellular Automata: 93–118, Santa Fe Institute Studies in the Sciences of Complexity, Oxford University Press.
- ↑ Естественный образец — объект, относительно часто возникающий в процессе развития случайной конфигурации.
- 1 2 3 Achim Flammenkamp. Top 100 of Game-of-Life Ash Objects. Проверено 5 ноября 2008.
- 1 2 3 4 Игра Жизнь (обзор Гарднера). Проверено 11 августа 2013. Архивировано 18 октября 2012 года.
- 1 2 3 4 5 Клумова И. Н. Игра «Жизнь» // Квант. — 1974. — № 9. — С. 26—30.
- ↑ Пекарня. Словарь Жизни.
- ↑ Не путать с космическим кораблём.
- 1 2 Bosch, R. A. (1999). “Integer programming and Conway's game of Life”. SIAM Review. 41 (3): 594—604. DOI:10.1137/S0036144598338252..
- ↑ Bosch, R. A. (2000). “Maximum density stable patterns in variants of Conway's game of Life”. Operations Research Letters. 27 (1): 7—11. DOI:10.1016/S0167-6377(00)00016-X..
- ↑ Smith, Barbara M. (2002), "A dual graph translation of a problem in ‘Life’", Principles and Practice of Constraint Programming - CP 2002, vol. 2470, Lecture Notes in Computer Science, Springer-Verlag, pp. 89–94, DOI 10.1007/3-540-46135-3_27 .
- ↑ Bosch, Robert; Trick, Michael (2004). “Constraint programming and hybrid formulations for three Life designs”. Annals of Operations Research. 130 (1—4): 41—56. DOI:10.1023/B:ANOR.0000032569.86938.2f..
- ↑ Cheng, Kenil C. K.; Yap, Roland H. C. (2006). “Applying ad-hoc global constraints with the case constraint to still-life”. Constraints. 11 (2—3): 91—114. DOI:10.1007/s10601-006-8058-9..
- ↑ Elkies, Noam D. (1998). "The still life density problem and its generalizations". Voronoi's Impact on Modern Science, Book I: 228–253, Proc. Inst. Math. Nat. Acad. Sci. Ukraine, vol. 21.
- ↑ J. Larrosa, E. Morancho and D. Niso (2005). “On the Practical use of Variable Elimination in Constraint Optimization Problems: 'Still-life' as a Case Study”. Journal of Artificial Intelligence Research. 23: 421—440.
- ↑ Neil Yorke-Smith. Maximum Density Still Life. Artificial Intelligence Center. SRI International.
- ↑ Number of stable n-celled patterns («still lifes») in Conway's game of Life
- ↑ Number of n-celled pseudo-still-lifes in Conway's game of Life
- ↑ Niemiec, Mark D. Life Still-Lifes. Архивировано 21 января 2013 года.
Внешние ссылки
- Николай Белюченко. Словарь Жизни. Архивировано 10 октября 2012 года.
- Stephen A. Silver. Life Lexicon. Архивировано 26 мая 2013 года.
Данная страница на сайте WikiSort.ru содержит текст со страницы сайта "Википедия".
Если Вы хотите её отредактировать, то можете сделать это на странице редактирования в Википедии.
Если сделанные Вами правки не будут кем-нибудь удалены, то через несколько дней они появятся на сайте WikiSort.ru .