WikiSort.ru - Не сортированное

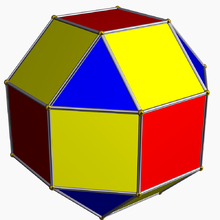
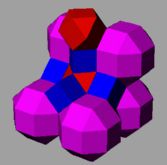
В геометрии скашивание — это операция в пространстве любой размерности, при которой срезаются рёбра и вершины правильного многогранника, создавая новые грани на месте каждого ребра и вершины. Операцию можно применять к правильным мозаикам и сотам. Операция также является спрямлением полного усечения многогранника.

Операция (для многогранников и мозаик) также называется расширением^[en] (согласно Стотт^[en]), поскольку эту операцию можно представить как движение граней (в сторону удаления от центра многогранника), а на месте образовавшихся щелей образуются новые грани.

Обозначения

Операция представляется расширенным cимволом Шлефлиl t_0,2{p,q,...}, или ${\displaystyle r{\begin{Bmatrix}p\\q\end{Bmatrix}}}$ , или rr{p,q,...}.

Для многогранников операция скашивания даёт последовательность многогранников от правильного многогранника до его двойственного.

Примеры многогранников и мозаик

Однородные многогранники и мозаики

	Многогранники			Мозаики
Коксетер	rTT	rCO	rID	rQQ	rHΔ
Нотация Конвея	eT	eC = eO	eI = eD	eQ	eH = eΔ
Расширенные многогранники	Тетраэдр	Куб или Октаэдр	Икосаэдр или Додекаэдр	Квадратная мозаика	Шестиугольная мозаика Треугольная мозаика
Рисунок
Вращающиеся

2-однородные многогранники

Коксетер	rrt{2,3}	rrs{2,6}	rrCO	rrID
Нотация Конвея	eP3	eA4	eaO = eaC	eaI = eaD
Расширенные многогранники	Треугольная призма или Треугольная бипирамида	Квадратная антипризма или Четырёхугольный трапецоэдр	Кубооктаэдр или Ромбододекаэдр	Икосододекаэдр или Ромботриаконтаэдр
Рисунок
Вращающиеся

См. также

• Однородный многогранник^[en]
• Однородный 4-мерный многогранник^[en]

Литература

• H.S.M. Coxeter. Chapter 8: Truncation, p. 210 Expansion // Regular Polytopes. — 3rd. — Dover edition, 1973. — P. 145—154. — ISBN 0-486-61480-8.
• Norman Johnson^[en] Uniform Polytopes, Manuscript (1991)
• N.W. Johnson^[en] : The Theory of Uniform Polytopes and Honeycombs, Ph.D. Dissertation, University of Toronto, 1966

Ссылки

• Weisstein, Eric W. Expansion (англ.) на сайте Wolfram MathWorld.
• George Olshevsky^[en]
• Truncation на Glossary for Hyperspace.

Для улучшения этой статьи желательно: Проверить качество перевода с иностранного языка. Исправить статью согласно стилистическим правилам Википедии.