WikiSort.ru - Не сортированное

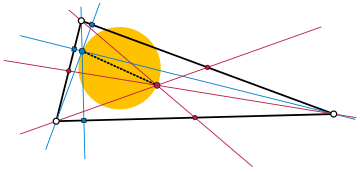
Ортоцентроидная окружность неравностороннего треугольника — это окружность, построенная на отрезке, соединяющем его ортоцентр и центроид, как на диаметре. Этот диаметр также содержит центр описанной окружности и центр окружности девяти точек треугольника и является частью прямой Эйлера.

Гвинанд (Guinand) в 1984 г. показал, что инцентр треугольника должен лежать внутри ортоцентроидной окружности, но не совпадать с центром девяти точек; то есть он должен попадать в открытый ортоцентроидный диск с вырезанным внутри центром девяти точек^{[1][2][3][4] [5]:pp. 451–452}.

Более того^[2], точка Ферма, точка Жергонна и точка Лемуана лежат в открытом ортоцентроидном диске с вырезанным внутри своим собственным центром (и могут быть в любой точке внутри него), тогда как вторая точка Ферма находится снаружи ортоцентроидного круга (и также может быть в любой точке снаружи). Возможные положения первой и второй точек Брокара также находятся в открытом ортоцентроидном диске^[6].

Квадрат диаметра ортоцентроидной окружности равен^[7]:p.102 ${\displaystyle D^{2}-{\tfrac {4}{9}}(a^{2}+b^{2}+c^{2}),}$ где a, b и c — длины сторон треугольника, D — диаметр описанной окружности.

Примечания