WikiSort.ru - Не сортированное

Алгебраические объекты

В этом разделе будет дано определение, подходящее для множеств с добавленной структурой, таких как группы, кольца, модули над фиксированным кольцом и т. д.

Пусть ${\displaystyle I}$  — направленное множество с отношением предпорядка ${\displaystyle \leqslant }$ и пусть каждому элементу ${\displaystyle i\in I}$ сопоставлен алгебраический объект ${\displaystyle X_{i}}$ , а каждой паре ${\displaystyle (i,\;j)}$ , ${\displaystyle i,\;j\in I}$ , в которой ${\displaystyle i\leqslant j}$ , сопоставлен гомоморфизм ${\displaystyle f_{ij}:X_{i}\to X_{j}}$ , причём ${\displaystyle f_{ii}}$  — тождественные отображения для любого ${\displaystyle i\in I}$ и ${\displaystyle f_{ik}=f_{jk}\circ f_{ij}}$ для любых ${\displaystyle i\leqslant j\leqslant k}$ из ${\displaystyle I}$ . Такую систему объектов и гомоморфизмов называют также направленной системой.

Тогда множество-носитель прямого предела направленной системы ${\displaystyle (X_{i},f_{ij})}$  — это фактормножество дизъюнктного объединения множеств-носителей ${\displaystyle X_{i}}$ по отношению эквивалентности:

${\displaystyle \varinjlim X_{i}=\bigsqcup _{i}X_{i}{\bigg /}\sim .}$

Здесь ${\displaystyle x_{i}\in X_{i}}$ и ${\displaystyle x_{j}\in X_{j}}$ эквивалентны, если существует такое ${\displaystyle k\in I}$ , что ${\displaystyle f_{ik}(x_{i})=f_{jk}(x_{j})}$ . Интуитивно, два элемента дизъюнктного объединения эквивалентны, тогда и только тогда, когда они «рано или поздно станут эквивалентными» в направленной системе. Более простая формулировка — это транзитивное замыкание отношения эквивалентности «каждый элемент эквивалентен своим образам», то есть ${\displaystyle x_{i}\sim \,f_{ik}(x_{i})}$ .

Из этого опредления легко получить канонические морфизмы ${\displaystyle \phi _{i}:X_{i}\rightarrow X}$ , отправляющие каждый элемент в его класс эквивалентности. Добавленную алгебраическую структуру на ${\displaystyle X}$ можно получить, исходя из знания этих гомоморфизмов.

Определение для произвольной категории

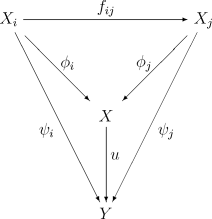
В произвольной категории прямой предел можно определить с помощью его универсального свойства. А именно, прямой предел направленной системы ${\displaystyle (X_{i},f_{ij})}$  — это объект ${\displaystyle X}$ категории, такой что выполняются следующие условия:

1. существует такое семейство отображений ${\displaystyle \phi _{i}:X_{i}\to X}$ , что ${\displaystyle \phi _{i}=\phi _{j}\circ f_{ij}}$ для любых ${\displaystyle i\leqslant j}$ ;
2. для любого семейства отображений ${\displaystyle \psi _{i}:X_{i}\to Y}$ , в произвольное множества ${\displaystyle Y}$ , для которого выполнены равенства ${\displaystyle \psi _{i}=\psi _{j}\circ f_{ij}}$ для любых ${\displaystyle i\leqslant j}$ , существует единственное отображение ${\displaystyle u:X\to Y}$ , что ${\displaystyle \psi _{i}=u\circ \phi _{i}}$ , для всех ${\displaystyle i\in I}$ .

Более общо, прямой предел направленной системы — это то же самое, что её копредел в категорном смысле.