WikiSort.ru - Не сортированное

Дикий узел — патологическое вложение окружности в пространство.

Дикие узлы можно найти в некоторых кельтских узорах.^{[источник не указан 1082 дня]}

Определение

Узел называется ручным, если он может быть «утолщён», то есть если существует его расширение до полнотория S ¹ × D ², допускающего вложение в 3-сферу. В теории узлов и в теории 3-многообразий^[en] часто слово «ручной» опускается.

Узлы, не являющиеся ручными, называются ди́кими и могут иметь патологическое поведение.

Примеры

Дикими являются узлы, содержащие так называемые дуги Фокса — Артина^[en] — некоторые простые дуги, полученные диким вложением в ${\displaystyle E^{3}}$ . Например, для дуги ${\displaystyle L_{1}}$ фундаментальная группа ${\displaystyle p_{1}}$ (${\displaystyle E^{3}L}$ ) нетривиальна, для дуги ${\displaystyle L_{2}}$ группа ${\displaystyle {\pi }_{1}(E^{3}/L)}$ тривиальна, но само ${\displaystyle E^{3}/L}$ не гомеоморфно дополнению в ${\displaystyle E^{3}}$ к точке^[1].

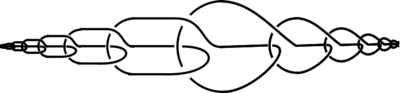
На рисунке приведён дикий узел с одной дикой (патологической) точкой. Легко построить дикий узел, содержащий несколько патологических точек, бесконечное число таких точек, и даже несчётное множество патологических точек. В книге Сосинского^[2] приведено построение дикого узла, патологические точки которого образуют канторово множество. Возможно представить и дикий узел, содержащее более сложное множество — ожерелье Антуана^[2].

Свойcтва

• Узел является ручным тогда и только тогда, когда он может быть представлен в виде конечной ломаной.
• Гладкие узлы являются ручными.

Вариации и обобщения

• Нетривиальные дикие узлы появляются и в сферах старших размерностей. Например по теореме о двойной надстройке, двойная надстройка над сферой Пуанкаре гомеоморфна стандартной сфере ${\displaystyle \mathbb {S} ^{5}}$ . При этом экватор двойной надстройки образует в ${\displaystyle \mathbb {S} ^{5}}$ дикой узел и его дополнение имеет нетривиальную фундаментальную группу.

См. также

• Дикая сфера

Примечания

Литература

• L. H. Kauffman. An invariant of regular isotopy // Transactions of the American Mathematical Society. — American Mathematical Society, 1990. — Vol. 318, № 2.
• А. Б. Сосинский. Узлы. Хронология одной математической теории. — Москва: МЦНМО, 2005. — ISBN 5-94057-220-0.

Это заготовка статьи по топологии. Вы можете помочь проекту, дополнив её.

Для улучшения этой статьи желательно: Проверить качество перевода с иностранного языка. Исправить статью согласно стилистическим правилам Википедии.