Теоремы об изоморфизме в алгебре — ряд теорем, связывающих понятия фактора, гомоморфизма и вложенного объекта. Утверждением теорем является изоморфизм некоторой пары групп, колец, модулей, линейных пространств, алгебр Ли или прочих алгебраических структур (в зависимости от области применения). Обычно насчитывают три теоремы об изоморфизме, называемые Первой (также основная теорема о гомоморфизме), Второй и Третьей. Хотя подобные теоремы достаточно легко следуют из определения фактора и честь их открытия никому особо не приписывается, считается, что наиболее общие формулировки дала Эмми Нётер.
Группы
Первая теорема
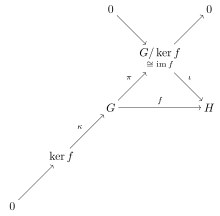
Пусть — гомоморфизм групп, тогда:
- Ядро φ — нормальная подгруппа в G;
- Образ φ — подгруппа в H;
- Образ φ изоморфен факторгруппе G / ker φ.
В частности, если гомоморфизм φ сюръективен (т.е. является эпиморфизмом), то группа H изоморфна факторгруппе G / ker φ.
Вторая теорема
Пусть G — группа, S — подгруппа в G, N — нормальная подгруппа в G, тогда:
- Произведение — подгруппа в G;
- Пересечение S ∩ N — нормальная подгруппа в S;
- Факторгруппы и S / (S ∩ N) изоморфны.
Третья теорема
Пусть G — группа, N и K — нормальные подгруппы в G такие, что K ⊆ N, тогда:
- N / K — нормальная подгруппа в G / K;
- Факторгруппа факторгрупп (G / K) / (N / K) изоморфна факторгруппе G / N.
Кольца
В данной области понятие нормальной подгруппы заменяется на понятие идеала кольца.
Первая теорема
Пусть гомоморфизм колец, тогда:
- Ядро φ — идеал в R;
- Образ φ — подкольцо в S;
- Образ φ изоморфен факторкольцу R / ker φ.
В частности, если гомоморфизм φ сюръективен (т.е. является эпиморфизмом), то кольцо S изоморфно факторкольцу R / ker φ.
Вторая теорема
Пусть R — кольцо, S — подкольцо в R, I — идеал в R, тогда:
- Сумма S + I — подкольцо в R;
- Пересечение S ∩ I — идеал в S;
- Факторкольца (S + I) / I и S / (S ∩ I) изоморфны.
Третья теорема
Пусть R — кольцо, A и B — идеалы в R такие, что B ⊆ A, тогда:
- A / B — идеал в R / B;
- Факторкольцо факторколец (R / B) / (A / B) изоморфно факторкольцу R / A.
Модули, абелевы группы и линейные пространства
Теоремы об изоморфизме абелевых групп и линейных пространств являются частным случаем теорем для модулей, которые и будут сформулированы. Для линейных пространств дополнительную информацию можно найти в статье «ядро линейного отображения».
Первая теорема
Пусть — гомоморфизм модулей, тогда:
- Ядро φ — подмодуль в M;
- Образ φ — подмодуль в N;
- Образ φ изоморфен фактормодулю M / ker φ.
Вторая теорема
Пусть M — модуль, S и T — подмодули в M, тогда:
- Сумма S + T — подмодуль в M;
- Пересечение S ∩ T — подмодуль в M;
- Фактормодуль (S + T) / T изоморфен фактормодулю S / (S ∩ T).
Третья теорема
Пусть M — модуль, S и T — подмодули в M такие, что T ⊆ S, тогда:
- S / T — подмодуль в M / T;
- Фактормножество фактормодулей (M / T) / (S / T) изоморфно фактормодулю M / S.
См. также
Данная страница на сайте WikiSort.ru содержит текст со страницы сайта "Википедия".
Если Вы хотите её отредактировать, то можете сделать это на странице редактирования в Википедии.
Если сделанные Вами правки не будут кем-нибудь удалены, то через несколько дней они появятся на сайте WikiSort.ru .




