Разбие́ние числа́ — это представление в виде суммы положительных целых чисел, называемых частями. При этом порядок следования частей не учитывается (в отличие от композиций), то есть разбиения, отличающиеся только порядком частей, считаются равными. В канонической записи разбиения части перечисляются в невозрастающем порядке.
Число разбиений натурального числа является одним из фундаментальных объектов изучения в теории чисел.
Примеры
Например, {3, 1, 1} или {3, 2} — разбиения числа 5, поскольку 5 = 3 + 1 + 1 = 3 + 2. Всего существует разбиений числа 5: {1, 1, 1, 1, 1}, {2, 1, 1, 1}, {2, 2, 1}, {3, 1, 1}, {3, 2}, {4, 1}, {5}.
Некоторые значения числа разбиений приведены в следующей таблице[1]:
| n | p(n) | Разбиения |
|---|---|---|
| 1 | 1 | {1} |
| 2 | 2 | {1, 1}, {2} |
| 3 | 3 | {1, 1, 1}, {2, 1}, {3} |
| 4 | 5 | {1, 1, 1, 1}, {2, 1, 1}, {2, 2}, {3, 1}, {4} |
| 5 | 7 | {1, 1, 1, 1, 1}, {2, 1, 1, 1}, {2, 2, 1}, {3, 1, 1}, {3, 2}, {4, 1}, {5} |
| 6 | 11 | |
| 7 | 15 | |
| 8 | 22 | |
| 9 | 30 | |
| 10 | 42 | |
| 20 | 627 | |
| 50 | 204 226 | |
| 100 | 190 569 292 | |
| 1000 | 24 061 467 864 032 622 473 692 149 727 991 |
Число разбиений
Производящая функция
Последовательность числа разбиений имеет следующую производящую функцию:
Эта формула была открыта Эйлером в 1740 году.
Пентагональная теорема Эйлера
Изучая производящую функцию последовательности , Эйлер сосредоточил внимание на её знаменателе, то есть, на произведении . Это бесконечное произведение при раскрытии скобок приобретает следующий вид:
Показатели степеней в правой части — числа вида где — целое число, а знак при равен . Для натуральных : — это пятиугольные числа.[2]
Согласно этому наблюдению, Эйлер предположил, что должна быть верна Пентагональная теорема:
Впоследствии эта теорема была доказана Эйлером. Она позволяет вычислять числа разбиений при помощи деления формальных степенны́х рядов.
Асимптотические формулы
Асимптотическое выражение для количества разбиений было получено Харди и Рамануджаном и впоследствии уточнено Радемахером. Оригинальное выражение Харди — Рамануджана[источник не указан 2278 дней]
- при
даёт, например, . Уточнение Радемахера представляет число разбиений в виде сходящегося ряда
где
Здесь суммирование ведётся по , взаимно простым с , а — сумма Дедекинда. Ряд сходится очень быстро.
Рекуррентные формулы
Количество разбиений числа на слагаемые, не превышающие , удовлетворяет рекуррентной формуле:
с начальными значениями:
- для всех
При этом количество всевозможных разбиений числа равно .
Диаграммы Юнга
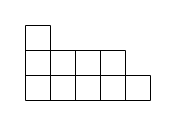
Разбиения удобно представлять в виде наглядных геометрических объектов, называемых диаграммами Юнга, в честь английского математика Альфреда Юнга[en]. Диаграмма Юнга разбиения — подмножество первого квадранта плоскости, разбитое на ячейки, каждая из которых представляет собой единичный квадрат. Ячейки размещаются в строки, первая строка имеет длину , над ней расположена строка длиной , и т. д. до -й строки длины . Строки выровнены по левому краю.
Более формально, диаграмма Юнга — это замыкание множества точек таких, что
- и
где обозначает целую часть .
В англоязычной литературе диаграммы Юнга часто изображают отражёнными относительно оси абсцисс.
Схожий объект, называемый диаграммой Феррерса, отличается тем, что
- вместо ячеек изображаются точки;
- диаграмма транспонируется: ряды и столбцы меняются местами.
Применение
Разбиения естественным образом возникают в ряде математических задач. Наиболее значимой из них является теория представлений симметрической группы, где разбиения естественно параметризуют все неприводимые представления. Суммы по всем разбиениям часто встречаются в математическом анализе.
См. также
Примечания
- ↑ Последовательность A000041 в OEIS
- ↑ Табачников С. Л., Фукс Д. Б. Математический дивертисмент. — МЦНМО, 2011. — ISBN 978-5-94057-731-7.
Литература
- Эндрюс Г. Теория разбиений. — М.: Наука, 1982. — 255 с.
- Макдональд И. Симметрические функции и многочлены Холла. — М.: Мир, 1985. — 224 с.
- Вайнштейн Ф. В. Разбиение чисел // Квант. — 1988. — № 11. — С. 19—25.
- Фукс Д. О раскрытии скобок, об Эйлере, Гауссе, Макдональде и об упущенных возможностях // Квант. — 1981. — № 8. — С. 12—20.
- Новая теория доказывает природу цифр.
- Бурман Ю. М. Разбиения и перестановки // Летняя школа «Современная математика». — 2004.
Данная страница на сайте WikiSort.ru содержит текст со страницы сайта "Википедия".
Если Вы хотите её отредактировать, то можете сделать это на странице редактирования в Википедии.
Если сделанные Вами правки не будут кем-нибудь удалены, то через несколько дней они появятся на сайте WikiSort.ru .
































![y<\sum _{{j=[x]}}^{{m}}k_{j},](https://wikimedia.org/api/rest_v1/media/math/render/svg/0e67b891995f8312a5dbf100bc4abf5ce5b8233b)
![[x]](https://wikimedia.org/api/rest_v1/media/math/render/svg/07548563c21e128890501e14eb7c80ee2d6fda4d)