WikiSort.ru - Не сортированное

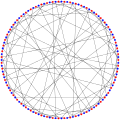
12-клетка Тата
Назван в честь	У. Т. Тата
Вершин	126
Рёбер	189
Радиус	6
Диаметр	6
Обхват	12
Автоморфизмы	12096
Хроматическое число	2
Хроматический индекс	3
Свойства	Кубический Клетка Гамильтонов Полусимметричный Двудольный

12-клетка Тата или граф Бенсона^[1] — это 3-регулярный граф с 126 вершинами и 189 рёбрами, названный в честь У. Т. Тата^[2].

12-клетка Тата является единственной (3-12)-клеткой (последовательность A052453 в OEIS). Граф открыл К. Т. Бенсон в 1966 году^[3]. Граф имеет хроматическое число 2 (двудольный), хроматический индекс 3, обхват 12 (как 12-клетки) и диаметр 6. Его число пересечений равно 170 и есть предположение, что этот граф является минимальным с данным числом пересечений^[4][5].

Построение

12-клетка Тата является кубическим гамильтоновым графом и его можно определить LCF-кодом [17, 27, −13, −59, −35, 35, −11, 13, −53, 53, −27, 21, 57, 11, −21, −57, 59, −17]^7[6].

Как доказали Коэн и Титс, есть, с точностью до изоморфизма, в точности два обобщённых шестиугольника порядка (2,2). Это разбитый шестиугольник Кэли H(2) и его двойственный (по точкам/прямым). Ясно, что оба имеют тот же самый граф инцидентности, который, фактически, изоморфен 12-клетке Тата^[1].

11-клетка Балабана может быть построена путём отрезания от 12-клетки Тата маленького поддерева и удаления получившихся вершин степени два^[7].

Алгебраические свойства

Автоморфизм группы 12-клетки Тата имеет порядок 12 096 и является полупрямым произведением проективной специальной унитарной группы^[en] PSU(3,3) с циклической группой Z/2Z^[1]. Группа действует транзитивно на рёбрах, но не на вершинах, что делает его полусимметричным графом, регулярным графом, который рёберно-транзитивен, но не вершинно транзитивен. Фактически, автоморфизм группы 12-клетки Тата сохраняет доли графа и действует просто на каждой из них. Такие графы называются бипримитивными и существует только пять кубических бипримитивных графов. Они называются графами Иванова — Иофиновой и они имеют порядки 110, 126, 182, 506 и 990^[8].

Все кубические полусимметричные графы, содержащие вплоть до 768 вершин, известны. Согласно Кондеру, Малничу, Марушичу и Поточнику 12-клетка Тата является единственным полусимметричным графом с 126 вершинами и пятым наименьшим возможным кубическим полусимметричным графом после графа Грея, графа Иванова — Иофиновой с 110 вершинами, графа Любляны и графа с 120 вершинами с обхватом 8^[9].

Характеристический многочлен 12-клетки Тата равен

${\displaystyle (x-3)x^{28}(x+3)(x^{2}-6)^{21}(x^{2}-2)^{27}.\ }$

Граф является единственным с этим характеристическим многочленом, поэтому 12-клетка определяется его спектром.

Галерея

• 
  Хроматическое число 12-клетки Тата равно 2.
• 
  Хроматический индекс 12-клетки Тата равен 3.

Примечания

Литература

Для улучшения этой статьи желательно: Проверить качество перевода с иностранного языка. Исправить статью согласно стилистическим правилам Википедии.