WikiSort.ru - Не сортированное

Нерешённые проблемы математики: Можно ли любой симплекс разбить на ограниченное число ортосхем?

Нерешённая гипотеза Гуго Хадвигера, что любой симплекс может быть разбит на ортосхемы^[en], используя число ортосхем, ограниченное функцией от размерности симплекса^[1]. Если гипотеза верна, то верно и более общее утверждение, что любой выпуклый многогранник можно разбить на ортосхемы.

Определения и утверждение

В этом контексте симплекс в ${\displaystyle d}$ -мерном евклидовом пространстве — это выпуклая оболочка ${\displaystyle d+1}$ точек, не лежащих в одной гиперплоскости. Например, 2-мерный симплекс, это просто треугольник (выпуклая оболочка трёх точек на плоскости), а 3-мерный симплекс, это тетраэдр (выпуклая оболочка четырёх точек в трёхмерном пространстве). Точки, которые образуют симплекс таким способом, называются вершинами.

Ортосхема — это специальный вид симплекса. В ней вершины могут быть соединены путём, любые два ребра которого перпендикулярны друг другу. Двухмерная ортосхема — это прямоугольный треугольник. Трёхмерную ортосхему можно построить из куба путём поиска пути из трёх рёбер куба, которые не лежат на одной и той же грани с последующим образованием выпуклой оболочки четырёх точек на этом пути.

Рассечение тела ${\displaystyle S}$ (которое может быть любым замкнутым множеством в евклидовом пространстве) — это представление ${\displaystyle S}$ в виде объединения других тел, внутренности которых не пересекаются. То есть, интуитивно, тела не перекрываются, хотя они могут иметь общие точки на границах. Например, куб может быть рассечён на шесть трёхмерных ортосхем. Аналогичный результат может быть распространён на более общие объекты — любой гиперкуб или гиперпрямоугольник в ${\displaystyle d}$ -мерном пространстве может быть рассечён на ${\displaystyle d!}$ ортосхем.

Гипотеза Хадвигера утверждает, что существует функция ${\displaystyle f}$ такая, что любой ${\displaystyle d}$ -мерный симплекс может быть рассечён на не более чем ${\displaystyle f(d)}$ ортосхем. Хадвигер изложил эту проблему в 1956^[2]. Гипотеза остаётся, в целом, нерешённой, хотя специальные случаи для малых значений ${\displaystyle d}$ известны^[1].

В пространствах малой размерности

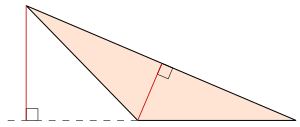
В двумерном пространстве любой треугольник можно рассечь на два прямоугольных треугольника путём опускания высоты на самую длинную сторону^[2].

В трёхмерном пространстве некоторые тетраэдры можно рассечь аналогично путём опускания высоты из вершины ${\displaystyle v}$ в точку ${\displaystyle p}$ на противоположной грани, соединения точки ${\displaystyle p}$ со сторонами грани перпендикулярно сторонам и использования путей из трёх отрезков, перпендикулярных друг другу — от точки ${\displaystyle v}$ к ${\displaystyle p}$ , от ${\displaystyle p}$ на сторону и, затем, в вершину грани ^[2]. Однако это построение не всегда работает. В частности, существуют тетраэдры, для которых основание ни одной высоты не лежит на гранях тетраэдра. Используя более сложное построение, Ленхард^[3] доказал, что любой тетраэдр можно рассечь не более чем на 12 ортосхем^[4]. Бём^[5] доказал, что это значение оптимально — существуют тетраэдры, которые нельзя рассечь на менее чем 12 ортосхем^[6]. В той же статье Бём также обобщает результат на трёхмерную сферическую геометрию и трёхмерную гиперболическую геометрию.

В четырёхмерном пространстве требуется не более 500 ортосхем^[7]. В пятимерном пространстве также требуется конечное число ортосхем, где-то около 12,5 миллионов. Снова это применимо к сферической и гиперболической геометриям, как и к евклидовому пространству^[8].

Гипотеза Хадвигера остаётся недоказанной для всех размерностей, больших пяти^[1].

Следствия

Любой выпуклый многогранник можно рассечь на симплексы. Таким образом, если гипотеза Хадвигера верна, любой выпуклый многогранник можно также рассечь на ортосхемы^[8].

Связанный результат — любую ортосхему можно рассечь на ${\displaystyle d}$ или ${\displaystyle d+1}$ меньших ортосхем^[9][10]. Таким образом, рассечения симплексов, допускающих разбиение на ортосхемы, могут иметь произвольно большое число ортосхем в рассечениях.

Примечания

Литература

Для улучшения этой статьи желательно: Проверить качество перевода с иностранного языка. Исправить статью согласно стилистическим правилам Википедии.