WikiSort.ru - Не сортированное

Плоская волна — волна, фронт которой имеет форму плоскости.

Фронт плоской волны неограничен по размерам, вектор фазовой скорости перпендикулярен фронту. Плоская волна является частным решением волнового уравнения и удобной моделью: такая волна в природе не существует, так как плоский фронт волны начинается в ${\displaystyle -{\mathcal {\infty }}}$ и заканчивается в ${\displaystyle +{\mathcal {\infty }}}$ , чего, очевидно, быть не может. Такая волна переносила бы бесконечную мощность, и на создание волны потребовалась бы бесконечная энергия. Польза модели плоской волны заключается в том, что волну со сложным (реальным) фронтом можно представить в виде набора (спектра) плоских волн с помощью преобразования Фурье по пространственным переменным.

Квазиплоская волна - волна, фронт которой близок к плоскому в ограниченной области. Если размеры области достаточно велики для рассматривамой задачи, то квазиплоскую волну можно приближённо считать плоской. Волну со сложным фронтом можно аппроксимировать набором локальных квазиплоских волн, векторы фазовых скоростей которых нормальны реальному фронту в каждой его точке. Примерами источников квазиплоских электромагнитных волн являются лазер, зеркальная и линзовая антенны: распределение фазы электромагнитного поля в плоскости, параллельной апертуре (излучающему отверстию), близко к равномерному. По мере удаления от апертуры фронт волны принимает сложную форму.

Определение

Уравнение любой волны является решением дифференциального уравнения, называемого волновым. Волновое уравнение для функции ${\displaystyle A}$ записывается в виде

${\displaystyle \Delta A({\vec {r}},t)={\frac {1}{v^{2}}}\,{\frac {\partial ^{2}A({\vec {r}},t)}{\partial t^{2}}}}$

где

• ${\displaystyle \Delta }$  — оператор Лапласа;
• ${\displaystyle A({\vec {r}},t)}$  — искомая функция;
• ${\displaystyle r}$  — радиус-вектор искомой точки;
• ${\displaystyle v}$  — скорость волны;
• ${\displaystyle t}$  — время.

Одномерный случай

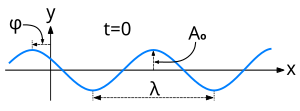
Плоская гармоническая волна задаётся уравнением

${\displaystyle A(x,t)=A_{o}\cos \left(kx-\omega t+\varphi _{0}\right)}$

где

• ${\displaystyle A(x,t)}$  — величина возмущения в данной точке пространства ${\displaystyle x}$ и времени ${\displaystyle t}$ ;
• ${\displaystyle A_{o}}$  — амплитуда волны;
• ${\displaystyle k}$  — волновое число;
• ${\displaystyle \omega }$  — круговая частота;
• ${\displaystyle \varphi _{0}}$  — начальная фаза колебаний.

Волну можно описать одним из уравнений

• ${\displaystyle A=A_{o}\cos \left(2\pi \left({\cfrac {x}{\lambda }}-{\cfrac {t}{T}}\right)+\varphi _{0}\right)}$

где

• ${\displaystyle \lambda }$  — период изменения функции в пространстве, длина волны;
• ${\displaystyle T}$  — период изменения функции во времени, период колебаний.

• ${\displaystyle A=A_{o}\cos \left(2\pi \left({\cfrac {x}{\lambda }}-ft\right)+\varphi _{0}\right)}$

где

• ${\displaystyle f}$  — частота колебаний.

• ${\displaystyle A=A_{o}\cos \left({\cfrac {2\pi }{\lambda }}(x-vt)+\varphi _{0}\right)}$

где

• ${\displaystyle v}$  — скорость движения волны.

Комплексная форма записи

Приведённые выше уравнения можно записать в так называемом комплексном виде:

${\displaystyle A(x,t)=A_{o}\,e^{i\left(kx-\omega t+\varphi _{0}\right)}.}$

или в многомерном случае

${\displaystyle A({\vec {r}},t)=A_{o}\,e^{i\left(({\vec {k}},{\vec {r}}\,)-\omega t+\varphi _{0}\right)}.}$

Правильность этой формулы легко проверить, применив формулу Эйлера. Вообще говоря, функция ${\displaystyle A({\vec {r}},t)}$ может быть как вещественной, так и комплексной функцией. Но так как в нашем реальном мире не существует комплексных чисел, то для расчётов всегда берётся реальная часть функции.

Стоит отметить, что из комплексной записи гармонической функции следует понятие комплексной амплитуды, равной ${\displaystyle {\widehat {A}}=A_{o}e^{i\varphi _{0}}.}$

Тогда ${\displaystyle A(x,t)={\widehat {A}}\,e^{i\left(({\vec {k}},{\vec {r}}\,)-\omega t\right)}.}$

Модуль комплексной функции даёт амплитуду колебаний, а аргумент — начальную фазу ${\displaystyle \varphi _{0}.}$

Экспоненциальная форма записи в некоторых случаях бывает удобнее тригонометрической.

Скорость волны

Энергия упругой плоской волны

Пусть дано, что ${\displaystyle A(x,t)=A_{o}\cos \left(\omega t-kx+\varphi _{0}\right).}$

Выделим в пространстве некий малый объём ${\displaystyle \Delta V}$ , настолько малый, что во всех точках этого объёма скорость движения частиц ${\displaystyle {\cfrac {\partial A}{\partial t}}}$ и деформацию ${\displaystyle {\cfrac {\partial A}{\partial x}}}$ можно считать постоянными.

Тогда данный объём обладает кинетической энергией

${\displaystyle \Delta W_{k}={\cfrac {\rho }{2}}\left({\cfrac {\partial A}{\partial t}}\right)^{2}\Delta V}$

и потенциальной энергией упругой деформации

${\displaystyle \Delta W_{p}={\cfrac {E}{2}}\left({\cfrac {\partial A}{\partial x}}\right)^{2}\Delta V={\cfrac {\rho v^{2}}{2}}\left({\cfrac {\partial A}{\partial x}}\right)^{2}\Delta V.}$

Полная энергия это

${\displaystyle W=\Delta W_{k}+\Delta W_{p}={\cfrac {\rho }{2}}{\bigg [}\left({\cfrac {\partial A}{\partial t}}\right)^{2}+v^{2}\left({\cfrac {\partial A}{\partial {x}}}\right)^{2}{\bigg ]}\Delta V.}$

Плотность энергии, соответственно, равна

${\displaystyle \omega ={\cfrac {W}{\Delta V}}={\cfrac {\rho }{2}}{\bigg [}\left({\cfrac {\partial A}{\partial t}}\right)^{2}+v^{2}\left({\cfrac {\partial A}{\partial {x}}}\right)^{2}{\bigg ]}=\rho A^{2}\omega ^{2}\sin ^{2}\left(\omega t-kx+\varphi _{0}\right).}$

Поляризация

Литература

• Савельев И.В. [Часть 2. Волны. Упругие волны.] // Курс общей физики / Под редакцией Гладнева Л.И., Михалина Н.А., Миртова Д.А.. — 3-е изд. — М.: Наука, 1988. — Т. 2. — С. 274-315. — 496 с. — 220 000 экз.

Примечания

См. также

• Сферическая волна
• Цилиндрическая волна
• Длина волны