WikiSort.ru - Не сортированное

Определение

Неотрицательная вещественнозначная интегрируемая функция K называется ядром. В большинстве случаев желательно, чтобы функция удовлетворяла ещё двум требованиям:

• Нормирование:

${\displaystyle \int _{-\infty }^{+\infty }K(u)\,du=1\,;}$

• Симметрия:

${\displaystyle K(-u)=K(u)\quad \forall u\,.}$

Если функция обладает первым свойством, то результатом ядерной оценки плотности действительно будет плотность вероятности. Второе свойство гарантирует, что среднее значение распределения равно среднему использованной выборки.

Если функция K является ядром, то ядром будет и функция K*(u) = λK(λu) при λ > 0. Данный результат позволяет выбрать масштаб, подходящий для имеющихся данных.

Часто используемые ядерные функции

В практике распространены несколько типов ядер: равномерное, треугольное, Епанечниково^[1], гауссово и проч.

Ниже дана таблица с перечнем часто используемых ядер. Если носитель ядра K ограничен, то для всех значений u вне носителя ${\displaystyle K(u)=0}$ .

Ядерные функции, K(u)			${\displaystyle \textstyle \int u^{2}K(u)du}$	${\displaystyle \textstyle \int K(u)^{2}du}$	Эффективность[2] относительно Епанечникова ядра
Равномерное	${\displaystyle K(u)={\frac {1}{2}}}$ Носитель: ${\displaystyle |u|\leq 1}$		${\displaystyle {\frac {1}{3}}}$	${\displaystyle {\frac {1}{2}}}$	92.9%
Треугольное	${\displaystyle K(u)=(1-|u|)}$ Носитель: 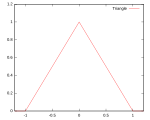${\displaystyle |u|\leq 1}$		${\displaystyle {\frac {1}{6}}}$	${\displaystyle {\frac {2}{3}}}$	98.6%
Епанечниково (параболическое)	${\displaystyle K(u)={\frac {3}{4}}(1-u^{2})}$ Носитель: ${\displaystyle |u|\leq 1}$		${\displaystyle {\frac {1}{5}}}$	${\displaystyle {\frac {3}{5}}}$	100%
Биквадратное	${\displaystyle K(u)={\frac {15}{16}}(1-u^{2})^{2}}$ Носитель: 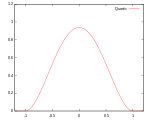${\displaystyle |u|\leq 1}$		${\displaystyle {\frac {1}{7}}}$	${\displaystyle {\frac {5}{7}}}$	99.4%
Триквадратное	${\displaystyle K(u)={\frac {35}{32}}(1-u^{2})^{3}}$ Носитель: ${\displaystyle |u|\leq 1}$		${\displaystyle {\frac {1}{9}}}$	${\displaystyle {\frac {350}{429}}}$	98.7%
Трикубическое	${\displaystyle K(u)={\frac {70}{81}}(1-{\left|u\right|}^{3})^{3}}$ Носитель: ${\displaystyle |u|\leq 1}$		${\displaystyle {\frac {35}{243}}}$	${\displaystyle {\frac {175}{247}}}$	99.8%
Гауссово	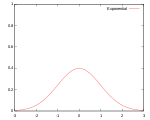${\displaystyle K(u)={\frac {1}{\sqrt {2\pi }}}e^{-{\frac {1}{2}}u^{2}}}$		${\displaystyle 1\,}$	${\displaystyle {\frac {1}{2{\sqrt {\pi }}}}}$	95.1%
Косинусоидальное	${\displaystyle K(u)={\frac {\pi }{4}}\cos \left({\frac {\pi }{2}}u\right)}$ Носитель: 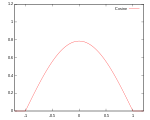${\displaystyle |u|\leq 1}$		${\displaystyle 1-{\frac {8}{\pi ^{2}}}}$	${\displaystyle {\frac {\pi ^{2}}{16}}}$	99.9%
Логистическое	${\displaystyle K(u)={\frac {1}{e^{u}+2+e^{-u}}}}$		${\displaystyle {\frac {\pi ^{2}}{3}}}$	${\displaystyle {\frac {1}{6}}}$	88.7%
Сигмоидальное	${\displaystyle K(u)={\frac {2}{\pi }}{\frac {1}{e^{u}+e^{-u}}}}$		${\displaystyle {\frac {\pi ^{2}}{4}}}$	${\displaystyle {\frac {2}{\pi ^{2}}}}$	84.3%
Сильвермана[3]	${\displaystyle K(u)={\frac {1}{2}}e^{-{\frac {|u|}{\sqrt {2}}}}\cdot \sin \left({\frac {|u|}{\sqrt {2}}}+{\frac {\pi }{4}}\right)}$		${\displaystyle 0}$	${\displaystyle {\frac {3{\sqrt {2}}}{16}}}$	не определена