Эллипсо́ид ине́рции (для точки O) — геометрическая фигура в виде поверхности второго порядка, которая характеризует тензор инерции твёрдого тела относительно точки O.
Тензор инерции и эллипсоид инерции
- Основная статья: Тензор инерции
Момент инерции тела дается общей формулой:
Тензор инерции для твердого тела представляется в виде симметричной матрицы
в которой элементы являются моментами инерции относительно различных осей:
|
|
|
Матрица тензора инерции может быть представлена в диагональном виде, и тогда диагональные элементы , , будут главными моментами инерции тела. Уравнение эллипсоида инерции тогда запишется как:
При этом координатные оси эллипсоида должны совпадать с главными осями тела.
Знание эллипсоида инерции позволяет найти момент инерции тела относительно любой оси, если только она проходит через центр эллипсоида. Для этого вдоль выбранной оси проводится радиус-вектор до пересечения с эллипсоидом инерции. Момент инерции тела относительно этой оси дается формулой:
, где - длина радиус-вектора.
Примеры эллипсоидов инерции

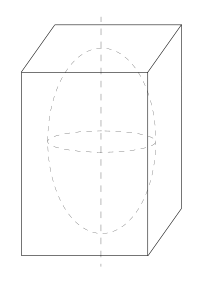
Прямоугольный параллелепипед
Пусть параллелепипед имеет размеры . Главные моменты инерции:
Примерный вид эллипсоида инерции представлен на иллюстрации.
Для расчета эллипсоида инерции бесконечно длинного тонкого стержня один из размеров считается много больше остальных, и эллипсоид вырождается в цилиндрическую поверхность.
Литература
- Сивухин Д.В. Общий курс физики. — 4-е изд. — М.: ФИЗМАТЛИТ; Изд-во МФТИ, 2005. — Т. 1. Механика. — С. 311. — 560 с. — ISBN 5-9221-0225-7.
- Лабораторный практикум по общей физике / А.Д.Гладун. — М.: МФТИ, 2004. — Т. 1. Механика. — С. 133. — 316 с. — ISBN 5-7417-0202-3.
- Ландау Л.Д., Лифшиц Е.М. Теоретическая физика. — 5-е изд. — М.: ФИЗМАТЛИТ, 2007. — Т. 1. Механика. — С. 131. — 224 с. — ISBN 978-5-9221-0819-5.
| Это заготовка статьи по механике. Вы можете помочь проекту, дополнив её. |
Данная страница на сайте WikiSort.ru содержит текст со страницы сайта "Википедия".
Если Вы хотите её отредактировать, то можете сделать это на странице редактирования в Википедии.
Если сделанные Вами правки не будут кем-нибудь удалены, то через несколько дней они появятся на сайте WikiSort.ru .