WikiSort.ru - Не сортированное

Метод подвижных клеточных автоматов
Подвижные клеточные автоматы активно меняют своих соседей за счет разрыва существующих связей между автоматами и образования новых связей (моделирование контактного взаимодействия)
Тип метода
Континуальный/Дискретный	Дискретный
Аналитический/Численный	Численный
Характеристики
Испытал влияние	Клеточный автомат, Метод дискретного элемента
Это метод	вычислительной механики

Метод подвижных клеточных автоматов (MCA, от англ. movable cellular automata) — это метод вычислительной механики деформируемого твердого тела, основанный на дискретном подходе. Он объединяет преимущества метода классических клеточных автоматов и метода дискретных элементов. Важным преимуществом метода МСА является возможность моделирования разрушения материала, включая генерацию повреждений, распространение трещин, фрагментацию и перемешивание вещества. Моделирование именно этих процессов вызывает наибольшие трудности в методах механики сплошных сред (метод конечных элементов, метод конечных разностей и др.), что является причиной разработки новых концепций, например, таких как перидинамика. Известно, что метод дискретных элементов весьма эффективно описывает поведение гранулированных сред. Особенности расчета сил взаимодействия между подвижными клеточными автоматами позволяют описывать в рамках единого подхода поведение как гранулированных, так и сплошных сред. Так, при стремлении характерного размера автомата к нулю формализм метода MCA позволяет перейти к классическим соотношениям механики сплошной среды.

Основные положения метода

В рамках метода MCA объект моделирования описывается как набор взаимодействующих элементов/автоматов. Динамика множества автоматов определяется силами их взаимодействия и правилами для изменения их состояния. Эволюция этой системы в пространстве и во времени определяется уравнениями движения. Силы взаимодействия и правила для связанных элементов определяются функциями отклика автомата. Эти функции задаются для каждого автомата. В течение движения автомата следующие новые параметры клеточного автомата рассчитываются: Rⁱ — радиус-вектор автомата; Vⁱ — скорость автомата; ${\displaystyle \omega }$ ⁱ — угловая скорость автомата; ${\displaystyle \theta }$ ⁱ — вектор поворота автомата; mⁱ — масса автомата; Jⁱ — момент инерции автомата.

Новая концепция — концепция соседей

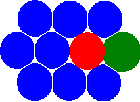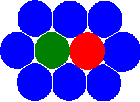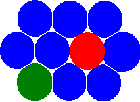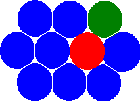
Новая концепция метода MCA основана на представлении состояния пары автоматов (связывает пару взаимодействующих автоматов) в дополнении к обычному состоянию отдельного автомата. Заметим, что учёт этого определения позволяет перейти от статической сеточной концепции к концепции соседей. В результате этого, автоматы имеют возможность менять своих соседей путём переключения состояния(зависимостей) пар.

Определение параметров состояния пары автоматов

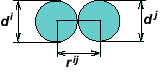
Ввод нового типа состояния требует нового параметра используемого в качестве критерия переключения в состояние связанные. Это определяется как параметр перекрытия автоматов h^ij. Итак, связь клеточных автоматов характеризуется величиной их перекрытия.

Начальная структура формируется установкой свойств особой связи между каждой парой соседних элементов.

Критерии переключения пары автоматов в состояние связанные

По сравнению с методом классических клеточных автоматами в методе MCA не только единичный автомат, но и также связи автоматов могут переключаться. В соответствии с концепцией бистабильных автоматов вводится два состояния пары (взаимосвязь):

Итак, изменение состояния связи пары определяется относительным движением автоматов, и среда, формируемая такими парами, может быть названа бистабильной средой.

Уравнения движения MCA

Эволюция MCA среды описывается следующими уравнениями трансляционного движения:

${\displaystyle {d^{2}h^{ij} \over dt^{2}}=\left({1 \over m^{i}}+{1 \over m^{j}}\right)p^{ij}+\sum _{k\neq j}C(ij,ik)\psi (\alpha _{ij,ik}){1 \over m^{i}}p^{ik}+\sum _{\ell \neq i}C(ij,j\ell )\psi (\alpha _{ij,j\ell }){1 \over m^{j}}p^{j\ell }}$

Здесь mⁱ это масса автомата i, p^ij это центральная сила действующая между автоматами i и j, C(ij, ik) это особый коэффициент ассоциированный с переносом параметра h из пары ij к ik, ψ(α_{ij, ik}) это угол между направлениями ij и ik.

Вращательные движения также могут быть учтены с точностью ограниченной размером клеточного автомата. Уравнения вращательного движения могут быть записаны следующим образом:

${\displaystyle {d^{2}\theta ^{ij} \over dt^{2}}=\left({q^{ij} \over J^{i}}+{q^{ji} \over J^{j}}\right)\tau ^{ij}+\sum _{k\neq j}S(ij,ik){q^{ik} \over J^{i}}\tau ^{ik}+\sum _{l\neq j}S(ij,jl){q^{jl} \over J^{j}}\tau ^{jl}}$

Здесь Θ^ij угол относительного поворота (это параметр переключения подобно h^ij трансляционного движения), q^ij(ji) это расстояние от центра автомата i(j) до точки контакта с автоматом j(i) (угловой момент), τ^ij это парное тангенциальное взаимодействие, S(ij, ik(jl)) это особый коэффициент ассоциированный с параметром переноса Θ от одной пары к другой (это похоже на C(ij, ik(jl)) из уравнений трансляционного движения).

Следует отметить, что уравнения полностью аналогичны уравнениям движения для многочастичной среды.

Определение деформации пары автоматов

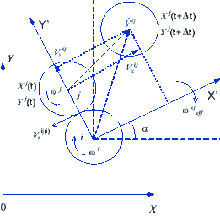
Смещение пары автоматов Безразмерный параметр деформации для смещения i j пары автоматов записывается как:

${\displaystyle \varepsilon ^{ij}={h^{ij} \over r_{0}^{ij}}={\left(q^{ij}+q^{ji}\right)-\left(d^{i}+d^{j}\right){\big /}2 \over \left(d^{i}+d^{j}\right){\big /}2}}$

В этом случае:

${\displaystyle \left(\Delta {\varepsilon ^{i(j)}}+\Delta {\varepsilon ^{j(i)}}\right){\left(d^{i}+d^{j}\right) \over 2}=V_{n}^{ij}\Delta {t}}$

где Δt временной шаг, V_n^ij — зависимая скорость. Вращение пары автоматов может быть посчитано аналогично с связью последнего смешения.

Описание необратимой деформации в методе MCA

Параметр ε^ij используется как мера деформации автомата i взаимодействующего с автоматом j. Где q^ij — расстояние от центра автомата i до точки его контакта с автоматом j; Rⁱ=dⁱ/2 (dⁱ — размер автомата i).

Например, титановый образец при циклическом нагружении (растяжение-сжатие). Диаграмма деформирования показана на следующем рисунке:

схема нагружения	Диаграмма деформирования
	(Красные точки — экспериментальные данные)

Преимущества метода MCA

Благодаря подвижности каждого автомата метод MCA позволяет напрямую учитывать такие события как:

• перемешивание масс
• эффект проникновения
• химические реакции
• интенсивные деформации
• фазовые превращения
• накопление повреждений
• фрагментация и трещины
• генерация и развитие повреждений

Используя различные граничные условия разных типов (жесткие, упругие, вязко-упругие, т.д.) можно имитировать различные свойства окружающей среды, содержащей моделируемую систему. Можно моделировать различные режимы механического нагружения (растяжение, сжатие, сдвиг, т.д.) с помощью настроек дополнительных состояний на границах.

Программное обеспечение

• Реализация MCA в рамках свободного пакета LIGGGHTS (в разработке).
• Программа для моделирования материалов в дискретно континуальном подходе «FEM+MCA»: Номер государственной регистрации в ОФАП (Патент): 50208802297 / Смолин А. Ю., Зелепугин С. А., Добрынин С. А.; заявитель и организация-разработчик ГОУ ВПО Томский государственный университет. — зарег. 28.11.2008; свидетельство ОФАП № 11826 от 01.12.2008.
• Программа для компьютерного моделирования деформации и разрушения наноструктурированных поверхностных слоёв металлокерамических композиционных материалов с явным учётом структурных элементов микро- и наноскопического масштабов на основе метода подвижных клеточных автоматов: Свидетельство о государственной регистрации программ для ЭВМ № 2016614245 / Шилько Е.В., Смолин А. Ю., Коростелев С. Ю., Димаки А. В., Астафуров С.В.; Правообладатель: Федеральное государственное бюджетное учреждение науки Институт физики прочности и материаловедения Сибирского отделения Российской академии наук (ИФПМ СО РАН); дата регистрации 19.04.2016.]

См. также

• Механика сплошных сред
• Механика разрушения твёрдых тел
• Теория упругости
• Перидинамика
• Компьютерное моделирование
• Метод дискретного элемента
• Клеточный автомат
• Метод конечных элементов
• Метод конечных разностей

Литература

• Psakhie, S.G.; Horie, Y.; Korostelev, S.Yu.; Smolin, A.Yu.; Dmitriev, A.I.; Shilko, E.V.; Alekseev, S.V. (1995). “Method of movable cellular automata as a tool for simulation within the framework of mesomechanics”. Russian Physics Journal. Springer New York. 38 (11): 1157-1168. DOI:10.1007/BF00559396. Используется устаревший параметр |coauthors= (справка)
• Псахье, С.Г.; Коростелев, С.Ю.; Смолин, А.Ю.; Дмитриев, А.И.; Шилько, Е.В.; Моисеенко, Д.Д.; Татаринцев, Е.М.; Алексеев, С.В. (1998). “Метод подвижных клеточных автоматов как инструмент физической мезомеханики материалов”. Физическая мезомеханика. Учреждение Российской академии наук Институт физики прочности и материаловедения Сибирского отделения РАН (ИФПМ СО РАН). 1 (1): 95-108. Проверено 2010-03-03. Используется устаревший параметр |coauthors= (справка)
• Псахье, С.Г.; Остермайер, Г.П.; Дмитриев, А.И.; Шилько, Е.В.; Смолин, А.Ю.; Коростелев, С.Ю. (2000). “Метод подвижных клеточных автоматов как новое направление дискретной вычислительной механики. I. Теоретическое описание”. Физическая мезомеханика. Учреждение Российской академии наук Институт физики прочности и материаловедения Сибирского отделения РАН (ИФПМ СО РАН). 3 (2): 5–13. Проверено 2010-03-03. Используется устаревший параметр |coauthors= (справка)
• Psakhie, S.G.; Horie, Y.; Ostermeyer, G.P.; Korostelev, S.Yu.; Smolin, A.Yu.; Shilko, E.V.; Dmitriev, A.I.; Blatnik, S.; Spegel, M.; Zavsek, S. (December 2001). “Movable cellular automata method for simulating materials with mesostructure” (PDF). Theoretical and Applied Fracture Mechanics. Elsevier Science Ltd. 37 (1–3): 311-334. DOI:10.1016/S0167-8442(01)00079-9. Архивировано из оригинала (PDF) 2011-07-19. Используется устаревший параметр |coauthors= (справка)
• Псахье, С.Г.; Смолин, А.Ю.; Стефанов, Ю.П.; Макаров, П.В.; Чертов, М.А. (2004). “Моделирование поведения сложных сред на основе совместного использования дискретного и континуального подходов”. Письма в ЖТФ. 30 (17): 7–13. Проверено 2010-03-03. Используется устаревший параметр |coauthors= (справка)
• Shimizu, Y. Numerical modeling in Micromechanics via Particle Methods. — 2004.
• Gnecco, E. Fundamentals of friction and wear on the Nanoscale. — 2007.
• Yunliang, Tan; Guirong, Teng; Haitao, Li. “MCA Model for Simulating the Failure of Microinhomogeneous Materials”. Journal of Nanomaterials. Hindawi Publishing Corporation. 2008: 1-7. DOI:10.1155/2008/946038. 946038. Используется устаревший параметр |coauthors= (справка)
• Фомин, В.М. Механика - от дискретного к сплошному. — Рос. акад наук, Сиб. отд-ние, Ин-т теоретической и прикладной механики им. С.А. Христиановича, 2008. — P. 344.
• Смолин, А.Ю.; Роман, Н.В.; Добрынин, С.А.; Псахье, С.Г. (2009). “О вращательном движении в методе подвижных клеточных автоматов”. Физическая мезомеханика. Учреждение Российской академии наук Институт физики прочности и материаловедения Сибирского отделения РАН (ИФПМ СО РАН). 12 (2): 17–22. Проверено 2010-03-03. Используется устаревший параметр |coauthors= (справка)
• Popov, Valentin L. Kontaktmechanik und Reibung (Ein Lehr- und Anwendungsbuch von der Nanotribologie bis zur numerischen Simulation). — Springer Berlin Heidelberg, 2009. — DOI:10.1007/978-3-540-88837-6. . DOI:10.1007/978-3-540-88837-6. |title= пусто или отсутствует (справка)
• Добрынин, С.А. Развитие метода подвижных клеточных автоматов для моделирования генерации и распространения упругих волн при контактном взаимодействии твердых тел. — Томск : Диссертация … кандидата физико-математических наук, 2010. — P. 130.
• Добрынин, Сергей. Компьютерное моделирование методом подвижных клеточных автоматов. — Saarbrücken Germany : LAP LAMBERT Academic Publishing, 2011. — P. 132.
• Shilko, E.V.; Psakhie S.G., Schmauder S., Popov V.L., Astafurov S.V., Smolin A.Yu. (March 2015). “Overcoming the limitations of distinct element method for multiscale modeling of materials with multimodal internal structure”. Computational Materials Science. Elsevier Science Ltd. 102: 267-285. DOI:10.1016/j.commatsci.2015.02.026. Используется устаревший параметр |coauthors= (справка)