WikiSort.ru - Не сортированное

Каса́тельная пряма́я — прямая, проходящая через точку кривой и совпадающая с ней в этой точке с точностью до первого порядка.

Строгое определение

• Пусть функция ${\displaystyle f\colon U(x_{0})\subset \mathbb {R} \to \mathbb {R} }$ определена в некоторой окрестности точки ${\displaystyle x_{0}\in \mathbb {R} }$ , и дифференцируема в ней: ${\displaystyle f\in {\mathcal {D}}(x_{0})}$ . Касательной прямой к графику функции ${\displaystyle f}$ в точке ${\displaystyle x_{0}}$ называется график линейной функции, задаваемый уравнением

  ${\displaystyle y=f(x_{0})+f'(x_{0})(x-x_{0}),\quad x\in \mathbb {R} }$ .

• Если функция ${\displaystyle f}$ имеет в точке ${\displaystyle x_{0}}$ бесконечную производную ${\displaystyle f'(x_{0})=\pm \infty ,}$ то касательной прямой в этой точке называется вертикальная прямая, задаваемая уравнением

  ${\displaystyle x=x_{0}.}$

Замечание

Прямо из определения следует, что график касательной прямой проходит через точку ${\displaystyle (x_{0},f(x_{0}))}$ . Угол ${\displaystyle \alpha }$ между касательной к кривой и осью Ох удовлетворяет уравнению

${\displaystyle \operatorname {tg} \,\alpha =f'(x_{0})=k,}$

где ${\displaystyle \operatorname {k} }$  — коэффициент наклона касательной. Производная в точке ${\displaystyle x_{0}}$ равна угловому коэффициенту касательной к графику функции ${\displaystyle y=f(x)}$ в этой точке.

Касательная как предельное положение секущей

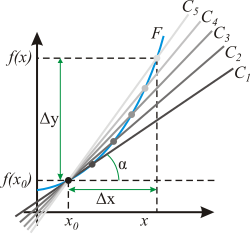
Пусть ${\displaystyle f\colon U(x_{0})\to \mathbb {R} }$ и ${\displaystyle x_{1}\in U(x_{0}).}$ Тогда прямая линия, проходящая через точки ${\displaystyle (x_{0},f(x_{0}))}$ и ${\displaystyle (x_{1},f(x_{1}))}$ задаётся уравнением

${\displaystyle y=f(x_{0})+{\frac {f(x_{1})-f(x_{0})}{x_{1}-x_{0}}}(x-x_{0}).}$

Эта прямая проходит через точку ${\displaystyle (x_{0},f(x_{0}))}$ для любого ${\displaystyle x_{1}\in U(x_{0}),}$ и её угол наклона ${\displaystyle \alpha (x_{1})}$ удовлетворяет уравнению

${\displaystyle \operatorname {tg} \,\alpha (x_{1})={\frac {f(x_{1})-f(x_{0})}{x_{1}-x_{0}}}.}$

В силу существования производной функции ${\displaystyle f}$ в точке ${\displaystyle x_{0},}$ переходя к пределу при ${\displaystyle x_{1}\to x_{0},}$ получаем, что существует предел

${\displaystyle \lim \limits _{x_{1}\to x_{0}}\operatorname {tg} \,\alpha (x_{1})=f'(x_{0}),}$

а в силу непрерывности арктангенса и предельный угол

${\displaystyle \alpha =\operatorname {arctg} \,f'(x_{0}).}$

Прямая, проходящая через точку ${\displaystyle (x_{0},f(x_{0}))}$ и имеющая предельный угол наклона, удовлетворяющий ${\displaystyle \operatorname {tg} \,\alpha =f'(x_{0}),}$ задаётся уравнением касательной:

${\displaystyle y=f(x_{0})+f'(x_{0})(x-x_{0}).}$

Касательная к окружности

Прямая, имеющая одну общую точку с окружностью и лежащая с ней в одной плоскости, называется касательной к окружности.

Вариации и обобщения

См. также

• Дифференцируемая функция
• Касательное пространство
• Нормаль, бинормаль
• Теорема о секущих

Литература

• Топоногов В. А. Дифференциальная геометрия кривых и поверхностей. — Физматкнига, 2012. — ISBN 9785891552135.
• Касательная // Энциклопедический словарь Брокгауза и Ефрона : в 86 т. (82 т. и 4 доп.). — СПб., 1890—1907.