| Граф МакГи | |
|---|---|
 | |
| Назван в честь | W. F. McGee |
| Вершин | 24 |
| Рёбер | 36 |
| Радиус | 4 |
| Диаметр | 4 |
| Обхват | 7 |
| Автоморфизмы | 32 |
| Хроматическое число | 3 |
| Хроматический индекс | 3 |
| Свойства |
кубический клетка гамильтонов |
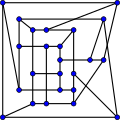
В теории графов графом МакГи, или (3-7)-клеткой, называется 3-регулярный граф с 24 вершинами и 36 рёбрами.[1]
Граф МакГи — это единственная (3,7)-клетка (наименьший кубический с обхватом 7). Он является наименьшей кубической клеткой, не являющейся графом Мура.
Впервые открытый Хорстом Саксом, но не опубликованный[2], граф назван в честь МакГи (W. F. McGee) , который опубликовал результат в 1960 году[3]. Позднее, в 1966 году, Уильям Томас Татт доказал, что это единственная (3,7)-клетка[4][5][6].
Известны наименьшие кубические графы с числом скрещиваний 1—8 (последовательность A110507 в OEIS), наименьший граф с числом скрещиваний 8 — это граф МакГи. Существует 5 неизоморфных кубических графов порядка 24 с числом скрещиваний 8[7], один из них — обобщённый граф Петерсена G(12,5), известный также как Граф Науру[8].
Граф МакГи имеет радиус 4, диаметр 4, хроматическое число 3 и хроматический индекс 3. Он также 3-вершинно-связен и 3-рёберно-связен.
Алгебраические свойства
Характеристический многочлен графа МакГи равен .
Автоморфизм группы графа МакГи имеет порядок 32 и не транзитивен относительно вершин — имеется две орбиты вершин длины 8 и 16. Граф МакГи — это наименьшая кубическая клетка, не являющаяся вершинно-транзитивной[9].
Галерея
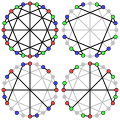
- Число скрещиваний графа МакГи равно 8.
- Хроматическое число графа МакГи равно 3.
- Хроматический индекс графа МакГи ракен 3.
- The Ациклический хроматический индекс графа МакГи равен 3.
- Альтернативное изображение графа МакГи.
Примечания
- ↑ Weisstein, Eric W. McGee Graph (англ.) на сайте Wolfram MathWorld.
- ↑ Kárteszi, F. "Piani finit ciclici come risoluzioni di un certo problemo di minimo." Boll. Un. Mat. Ital. 15, 522-528, 1960
- ↑ McGee, W. F. "A Minimal Cubic Graph of Girth Seven." Canad. Math. Bull. 3, 149-152, 1960
- ↑ Tutte, W. T. Connectivity in Graphs. Toronto, Ontario: University of Toronto Press, 1966
- ↑ Wong, P. K. "Cages--A Survey." J. Graph Th. 6, 1-22, 1982
- ↑ Brouwer, A. E.; Cohen, A. M.; and Neumaier, A. Distance Regular Graphs. New York: Springer-Verlag, p. 209, 1989
- ↑ Pegg, E. T. and Exoo, G. "Crossing Number Graphs." Mathematica J. 11, 2009
- ↑ Weisstein, Eric W. Graph Crossing Number (англ.) на сайте Wolfram MathWorld.
- ↑ Bondy, J. A. and Murty, U. S. R. Graph Theory with Applications. New York: North Holland, p. 237, 1976.
Для улучшения этой статьи желательно: |
Данная страница на сайте WikiSort.ru содержит текст со страницы сайта "Википедия".
Если Вы хотите её отредактировать, то можете сделать это на странице редактирования в Википедии.
Если сделанные Вами правки не будут кем-нибудь удалены, то через несколько дней они появятся на сайте WikiSort.ru .