WikiSort.ru - Не сортированное

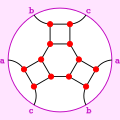
Граф Франклина
Назван в честь	Филип Франклин[en]
Вершин	12
Рёбер	18
Радиус	3
Диаметр	3
Обхват	4
Автоморфизмы	48 (Z/2Z×S4)
Хроматическое число	2
Хроматический индекс	3
Род	1
Свойства	Кубический Гамильтонов Двудольный Без треугольников Совершенный Вершинно-транзитивный

В теории графов граф Франклина — это 3-регулярный граф с 12 вершинами и 18 рёбрами^[1].

Граф назван именем Филипа Франклина^[en], опровергшего гипотезу Хивуда о числе цветов, необходимых для раскраски двумерных поверхностей, разделённых на ячейки при вложении графа^[2][3]. Согласно гипотезе Хивуда максимальное хроматическое число карты на бутылке Клейна должно равняться семи, однако Франклин доказал, что для данного графа шести цветов всегда достаточно. Граф Франклина может быть вложен в бутылку Клейна так, что он образует карту, требующую шесть цветов, что показывает, что в некоторых случаях шести цветов достаточно. Это вложение является Петри двойственным вложения в проективную плоскость (вложение показано ниже).

Граф является гамильтоновым и имеет хроматическое число 2, хроматический индекс 3, радиус 3, диаметр 3 и обхват 4. Он является также вершинно 3-связным и рёберно 3-связным совершенным графом.

Алгебраические свойства

Группа автоморфизмов графа Франклина имеет порядок 48 и изоморфна Z/2Z×S₄, прямому произведению циклической группы Z/2Z и симметрической группы S₄. Группа действует транзитивно на вершинах графа.

Характеристический многочлен графа Франклина равен

${\displaystyle (x-3)(x-1)^{3}(x+1)^{3}(x+3)(x^{2}-3)^{2}.\ }$

Галерея

• 
  Хроматическое число графа Франклина равно 2.
• 
  Хроматический индекс графа Франклина равен 3.
• 
  Альтернативный рисунок графа Франклина.
• 
  Граф Франклина, вложенный в проективную плоскость как усечённый полуоктаэдр^[en].

Примечания

Литература

• P. Franklin. A Six Color Problem // J. Math. Phys.. — 1934. — Т. 13. — С. 363-379.