WikiSort.ru - Не сортированное

Моноидальная категория (или тензорная категория) — категория C, снабженная бифунктором

⊗ : C × C → C,

который ассоциативен с точностью до естественного изоморфизма, а также объектом I, который является единицей для ⊗ также с точностью до естественного изоморфизма. Также на естественные изоморфизмы накладываются некоторые дополнительные условия. В моноидальной категории можно дать определение моноида, обобщающее свойства моноида из общей алгебры. На самом деле, обычные моноиды — это моноиды в категории множеств с прямым произведением в качестве моноидального произведения.

Обычное тензорное произведение делает векторные пространства, абелевы группы и модули моноидальными категориями, произвольные моноидальные категории можно рассматривать как обобщение этих примеров.

Определение

Формально, моноидальная категория — это категория ${\displaystyle \mathbf {C} }$ , снабжённая:

• бифунктором ${\displaystyle \otimes \colon \mathbf {C} \times \mathbf {C} \to \mathbf {C} }$ , называемым как тензорное произведение или моноидальное произведение,
• объектом ${\displaystyle I}$ , называемым единицей или тождественным объектом,
• тремя естественными изоморфизмами, выражающими тот факт, что операция тензорного произведения
  • ассоциативна: существует естественный изоморфизм (так называемый ассоциатор) ${\displaystyle \alpha }$ , ${\displaystyle \alpha _{A,B,C}\colon (A\otimes B)\otimes C\to A\otimes (B\otimes C)}$ ,
  • ${\displaystyle I}$ является единицей: существуют два естественных изоморфизма ${\displaystyle \lambda }$ и ${\displaystyle \rho }$ , ${\displaystyle \lambda _{A}\colon I\otimes A\to A}$ и ${\displaystyle \rho _{A}\colon A\otimes I\to A}$ .

На эти естественные изоморфизмы наложены дополнительные условия:

• для всех ${\displaystyle A}$ , ${\displaystyle B}$ , ${\displaystyle C}$ , ${\displaystyle D}$ в ${\displaystyle \mathbf {C} }$ следующая пятиугольная диаграмма коммутативна:

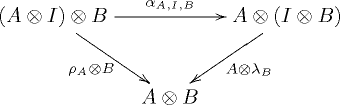
• для всех ${\displaystyle A}$ и ${\displaystyle B}$ в ${\displaystyle \mathbf {C} }$ треугольная диаграмма коммутативна:

Из этих условий следует, что любая диаграмма этого типа (то есть диаграмма, стрелки которой составлены из ${\displaystyle \alpha }$ , ${\displaystyle \lambda }$ , ${\displaystyle \rho }$ , единицы и тензорного произведения) коммутативна: это составляет предмет теоремы о когерентности Маклейна. Например, несколькими применениями ассоциатора легко показать, что ${\displaystyle (A_{N}\otimes A_{N-1})\otimes \cdots )\otimes A_{2})\otimes A_{1})}$ и ${\displaystyle (A_{N}\otimes (A_{N-1}\otimes \cdots \otimes (A_{2}\otimes A_{1})}$ изоморфны. Ассоциаторы можно применять в разном порядке (например, на диаграмме приведено два способа для N=4), но из теоремы о когерентности следует, что разные последовательности применений задают одно и то же отображение.

Строго моноидальная категория — это категория, для которой естественные изоморфизмы α, λ, ρ — тождественные.

Примеры

• Любая категория с конечными произведениями моноидальна, с категорным произведением в качестве моноидального произведения и терминальным объектом в качестве единицы. Такую категорию иногда называют декартово моноидальной категорией. Например:
  • ${\displaystyle \mathbf {Set} }$  — категория множеств с декартовым произведением и одноэлементным множеством в качестве единицы.
• Любая категория с конечными копроизведениями также является моноидальной с копроизведением и начальным объектом в качестве единицы.
• R-Mod, категория модулей над коммутативным кольцом R — моноидальна с тензорным произведением ⊗_R и кольцом R (понимаемым как модуль над самим собой) в качестве единицы.
• Категория эндофункторов (функторов в себя) в категории C — строгая моноидальная категория с композицией функторов в качестве операции произведения.

См. также

• Моноидальный функтор
• Обогащённая категория

Примечания

• Kelly, G. Max (1964). «On MacLane’s Conditions for Coherence of Natural Associativities, Commutativities, etc.» — Journal of Algebra 1, 397—402
• Kelly, G. Max. Basic Concepts of Enriched Category Theory. — Cambridge University Press, 1982.
• Mac Lane, Saunders (1963). «Natural Associativity and Commutativity». — Rice University Studies 49, 28-46.
• Маклейн С. Глава 7. Моноиды // Категории для работающего математика = Categories for the working mathematician / Пер. с англ. под ред. В. А. Артамонова. — М.: Физматлит, 2004. — С. 188—221. — 352 с. — ISBN 5-9221-0400-4.