WikiSort.ru - Не сортированное

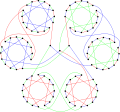
Граф Хортона
Граф Хортона
Назван в честь	Джозеф Хортон
Вершин	96
Рёбер	144
Радиус	10
Диаметр	10
Обхват	6
Автоморфизмы	96 (Z/2Z×Z/2Z×S4)
Хроматическое число	2
Хроматический индекс	3
Свойства	кубический двудольный

Граф Хортона — это 3-регулярный граф с 96 вершинами и 144 рёбрами, открытый Джозефом Хортоном^[1]. Бонди и Мурти опубликовали в 1976 этот граф в качестве контрпримера гипотезе Тата, что любой кубический 3-связный двудольный граф является гамильтоновым^[2][3].

Связанные графы

После публикации графа Хортона были найдены некоторые другие меньшие контрпримеры Тата. Среди них — граф с 92 вершинами, опубликованный Хортоном в 1982, граф с 78 вершинами, который опубликовал Оуэнс в 1983, и два графа Эллингхама – Хортона^[en] (с 54 и 78 вершинами)^[4][5].

Первый граф Эллингхама – Хортона был опубликован Эллингхамом в 1981 и имел 78 вершин^[6]. В то время это был самый маленький известный контрпример гипотезе Тата. Второй граф был опубликован Эллингхамом и Хортоном в 1983 и он имеет 54 вершин^[7]. Никаких меньших негамильтоновых кубических 3-связных двудольных графов в настоящее время не известно.

Свойства

Поскольку граф Хортона, не являясь гамильтоновым, имеет много длинных циклов, он является хорошей тестовой базой для программ поиска гамильтоновых циклов^[8].

Граф Хортона имеет хроматическое число 2, хроматический индекс 3, радиус 10, диаметр 10 и обхват 6. Он также является рёберно 3-связным графом.

Алгебраические свойства

Группа автоморфизмов графа Хортона имеет порядок 96 и изоморфна Z/2Z×Z/2Z×S₄, прямому произведению четверной группы Клейна и симметрической группы S₄.

Характеристический многочлен графа Хортона равен ${\displaystyle (x-3)(x-1)^{14}x^{4}(x+1)^{14}(x+3)(x^{2}-5)^{3}(x^{2}-3)^{11}(x^{2}-x-3)(x^{2}+x-3)}$ ${\displaystyle (x^{10}-23x^{8}+188x^{6}-644x^{4}+803x^{2}-101)^{2}}$ ${\displaystyle (x^{10}-20x^{8}+143x^{6}-437x^{4}+500x^{2}-59)}$ .

Галерея

• 
  Хроматическое число графа Хортона равно 2.
• 
  Хроматический индекс графа Хортона равен 3.
• 
  Граф Эллингтона – Хортона^[en], наименьший контрпример гипотезы Тата.

Примечания

Литература

Для улучшения этой статьи желательно: Проверить качество перевода с иностранного языка. Исправить статью согласно стилистическим правилам Википедии.