WikiSort.ru - Не сортированное

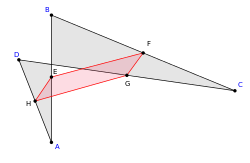
Теоре́ма Вариньо́на — геометрический факт, доказанный Пьером Вариньоном и утверждающий, что середины сторон произвольного четырёхугольника являются вершинами параллелограмма. Точнее

Четырёхугольник, вершины которого совпадают с серединами сторон произвольного четырёхугольника, является параллелограммом, стороны которого параллельны диагоналям исходного четырёхугольника.

Параллелограмм, образованный серединами сторон, иногда называется вариньоновским или вариньоновым.

Следствия

• Центр параллелограмма Вариньона лежит на середине отрезка, соединяющего середины сторон исходного четырёхугольника (в этой же точке пересекаются отрезки, соединяющие середины противоположных сторон — диагонали вариньоновского параллелограмма).
• Периметр параллелограмма Вариньона равен сумме диагоналей исходного четырёхугольника.
• Площадь параллелограмма Вариньона равна половине площади исходного четырёхугольника.
• Для прямоугольника и равнобедренной трапеции параллелограммом Вариньона является ромб, а для ромба — прямоугольник.
• Параллелограмм Вариньона является ромбом тогда и только тогда, когда в исходном четырехугольнике 1) диагонали равны 2) бимедианы перпендикулярны.
• Параллелограмм Вариньона является прямоугольником тогда и только тогда, когда в исходном четырехугольнике: 1) диагонали перпендикулярны; 2) бимедианы равны.
• Параллелограмм Вариньона является квадратом тогда и только тогда, когда в исходном четырехугольнике 1) диагонали равны и перпендикулярны; 2) бимедианы равны и перпендикулярны.

Для улучшения этой статьи по математике желательно: Найти и оформить в виде сносок ссылки на независимые авторитетные источники, подтверждающие написанное. Исправить статью согласно стилистическим правилам Википедии.

Другие следствия теоремы Вариньона

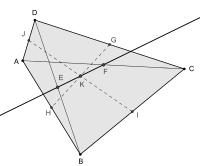
• Теоремы о средних линиях четырёхугольника

Пусть G, H, I, J — середины сторон выпуклого четырёхугольника ABCD, а E, F — середины его диагоналей. Назовем три отрезка GH, IJ, EF соответственно первой, второй и третьей средними линиями четырёхугольника.

• Теорема Вариньона (геометрия)^[1]:
  • Четырёхугольники GIHJ, EHFG, JEIF являются параллелограммами и называются параллелограммами Вариньона. Первый из них назовем большим параллелограммом Вариньона

• • Центры всех трех параллелограммов Вариньона лежат на середине отрезка, соединяющего середины сторон исходного четырёхугольника (в этой же точке пересекаются отрезки, соединяющие середины противоположных сторон — диагонали вариньоновского параллелограмма).

• • Периметр большого параллелограмма Вариньона ${\displaystyle GIHJ}$ равен сумме диагоналей исходного четырёхугольника ${\displaystyle ABCD}$ .

• • Площадь большого параллелограмма Вариньона ${\displaystyle GIHJ}$ равна половине площади исходного четырёхугольника ${\displaystyle ABCD}$ , то есть

${\displaystyle S_{GIHJ}={\frac {1}{2}}S_{ABCD}}$ .

• • Площадь исходного четырёхугольника ${\displaystyle ABCD}$ равна произведению первой ${\displaystyle GH}$ и второй ${\displaystyle IJ}$ средних линий четырёхугольника на синус угла ${\displaystyle \phi }$ между ними, то есть

${\displaystyle S_{ABCD}=GH\cdot IJ\sin \phi }$ .

• • Обобщенная теорема Ньютона. Средние линии четырёхугольника и отрезок, соединяющий середины диагоналей этого четырехугольника, пересекаются в одной точке и делятся ею пополам.

• • Сумма квадратов средних линий четырёхугольника и отрезка, соединяющего середины диагоналей этого четырехугольника, равна четверти суммы квадратов всех его сторон и диагоналей:

${\displaystyle GH^{2}+IJ^{2}+EF^{2}={\frac {1}{4}}(AB^{2}+BC^{2}+CD^{2}+DA^{2}+BD^{2}+AC^{2})}$ .

• • Если исходный четырехугольник — параллелограмм, то его третья средняя линия вырождается в точку (в точку пересечения его диагоналей), а первая и вторая его средние линии пересекаются в точке пересечения его диагоналей. В этой точке две его диагонали и две его средние линии делятся пополам.

См. также

• Прямая Гаусса
• Теорема Ньютона (планиметрия)
• Четырехугольник

Примечания

Это заготовка статьи по геометрии. Вы можете помочь проекту, дополнив её.