
Солитер — это настольная игра для одного игрока, в которой переставляются колышки на доске с отверстиями. Некоторые комплекты используют шарики и доски с выемками. В США игра имеет название Peg Solitaire (колышковый солитер), а название Солитер относится к пасьянсу. В Великобритании игра известна под именем Solitaire (солитер), а карточная игра называется Patience (пасьянс). В некоторых местах, в частности, в Индии, игра носит название Brainvita.
Первое упоминание об игре можно выявить во дворе Людовика XIV в 1697. Этим годом помечена гравюра Клода Огюста Берея Анна де Роан Шабо, принцесса де Субиз, на которой изображена принцесса, играющая в солитер. В августе 1697 во французском литературном журнале Mercure galant было напечатано описание доски, правила и примеры задач. Это первое известное упоминание игры в печати.
В стандартной игре всё поле заполняется колышками, за исключением центрального отверстия. Цель игры — освободить всю доску от колышек, оставив последний колышек в центре доски.
Доска
Существуют две традиционные доски для игры ('.' В качестве начального колышка, 'o' в качестве пустого отверстия):
Игра

Разрешённым ходом является прыжок колышка через смежный колышек на свободное отверстие сразу после второго колышка (как в шашках, но движение происходит вертикально или горизонтально, по диагонали двигаться нельзя), затем колышек, через который перепрыгнули, удаляется.
Обозначения в диаграммах ниже:
• колышек в отверстии
* передвигаемый колышек
o пустое отверстие
¤ отверстие, с которого был сделан ход
* конечная позиция колышка
o отверстие удалённого колышка.
Тогда допустимыми ходами во всех четырёх направлениях будут:
* • o → ¤ o * прыжок вправо
o • * → * o ¤ прыжок влево
* ¤ • → o прыжок вниз o *
o * • → o прыжок вверх * ¤
На английской доске первыми тремя ходами могут быть:
• • • • • • • • • • • •
• * • • ¤ • • o • • * •
• • • • • • • • • • o • • • • ¤ o * • • • • o o o • • •
• • • o • • • • • • * • • • • • • • • • • • • • ¤ • • •
• • • • • • • • • • • • • • • • • • • • • • • • • • • •
• • • • • • • • • • • •
• • • • • • • • • • • •
Стратегия
Легко пойти неверным путём, и обнаружить, что два или три пустых отверстия отделяют одинокий колышек. Многие люди так и не смогли решить задачу.
Имеется множество различных решений для стандартной задачи, и для их описания дадим отверстиям буквенные обозначения:
English European
a b c a b c
d e f y d e f z
g h i j k l m g h i j k l m
n o p x P O N n o p x P O N
M L K J I H G M L K J I H G
F E D Z F E D Y
C B A C B A
Зеркальное обозначение полей используется, кроме всего прочего, поскольку на европейской доске в одном из семейства альтернативных игр игра начинается с некоторого отверстия в произвольном месте и должна закончиться в зеркальном отверстии. На английской доске альтернативные игры начинаются и кончаются в том же самом отверстии.
В европейской версии игры не существует решения с начальным пустым полем в центре, если только не разрешить диагональные ходы. Это легко понять, если учесть аргументы Ганса Цантема (Hans Zantema). Разметим позиции доски буквами A, B и C следующим образом:
A B C
A B C A B
A B C A B C A
B C A B C A B
C A B C A B C
B C A B C
A B C
Будем считать число колышков в позициях каждого типа. Если начальная пустая позиция находится в центре, число позиций A равно 12, позиций B тоже 12 (всего 13, но одна свободна), число позиций C тоже 12. После каждого хода число колышков группы A уменьшается или увеличивается на единицу, то же самое происходит с позициями групп B и C. Таким образом, после чётного числа ходов все эти три числа чётны, а после нечётного — нечётны. Таким образом, конечная позиция, в которой остаётся только один колышек, получена быть не может — группа, где окажется колышек, будет иметь сумму единица, в то время как другие два должны иметь сумму ноль.
Есть, однако, некоторые другие конфигурации, в которых можно одно свободное отверстие довести до единственного колышка.
Для решения головоломки полезна тактика, при которой вся доска делится на тройки, а затем тройки удаляются с помощью дополнительного колышка, катализатора. В приведенном примере * является катализатором:
* • o ¤ o * o * • * o ¤ • → • → o → o • • ¤ o
Такая техника может быть использована для трёх колышек в ряд, для блоков 2•3 и фигуры L из 6 колышек (3 в одну сторону и 4 перпендикулярно).
Существуют игры, начинающиеся с двух пустых позиций и завершающиеся двумя колышками в этих позициях. Также можно начинать с одной заранее выбранной позиции и завершать в другой заранее выбранной позиции. На английской доске пустое отверстие может быть в любом месте, а завершиться игра должна в этой же позиции, либо в одной из трёх добавочных допустимых позиций. Так, если начальное пустое поле было в точке a, игра должна завершиться единственным колышком в позициях a, p, O или C.
Изучение игры в солитер
Полный анализ игры проведён в книге «Winning Ways for your Mathematical Plays» (ISBN 0-12-091102-7 в Великобритании и ISBN 1-56881-144-6 в США) (том 4, второе издание). В книге введена нотация, названная функция пагоды, которая является сильным средством для доказательства невозможности решения данной (обобщённой) задачи солитера. Задача поиска такой функции формулируется как задача линейного программирования и она разрешима за полиномиальное время (смотрите Kiyomi и Matsui 2001). Ухара и Ивата (Uehara, Iwata, 1990) изучали обобщённые Hi-Q задачи, которые эквивалентны задачам солитера и показали их NP-полноту. Авис и Деза (Avis, Deza, 1996) сформулировали задачу солитера как комбинаторную задачу оптимизации и обсуждали свойство области допустимых решений, называемой конусом солитера. Кийоми и Мацуи (Kiyomi, Matsui, 2001) предложили эффективный метод решения задач солитера.
Неопубликованное исследование 1989 года об обобщённой версии игры на английской доске показало, что каждая допустимая задача в обобщённой игре имеет 29 различных решений, исключая симметрию, поскольку английская доска содержит 9 различных 3×3 подквадратов. Это исследование дало нижнюю границу размера возможных задач 'обратных позиций', в которых первоначально занятые отверстия становятся занятыми, и наоборот. Любое решение такой задачи должно состоять минимум из 11 ходов, независимо от точных формулировок задачи.
С помощью алгебры можно доказать, что имеется только 5 фиксированных точек, где игра может завершиться успешно с одним колышком[1].
Решения для английской версии игры
Кратчайшее решение стандартной английской версии игры состоит из 18 ходов, если считать многократные перепрыгивания за один ход:
| Shortest solution to English peg solitaire |
|---|
e-x l-j c-k
• • • • • • • • • • • ¤
• * • • ¤ • • o • • o o
• • • • • • • • • • o • • • • • • * o ¤ • • • • • * o •
• • • o • • • • • • * • • • • • • • • • • • • • • • • •
• • • • • • • • • • • • • • • • • • • • • • • • • • • •
• • • • • • • • • • • •
• • • • • • • • • • • •
P-f D-P G-I J-H
• • o • • o • • o • • o
• o * • o • • o • • o •
• • • • o o • • • • • o o • • • • • o o • • • • • o o •
• • • • ¤ • • • • • • * • • • • • • • • • • • • • • • •
• • • • • • • • • • • o • • • • • • * o ¤ • • • ¤ o * o
• • • • • ¤ • • o • • o
• • • • • • • • • • • •
m-G-I i-k g-i L-J-H-l-j-h
• • o • • o • • o • • o
• o • • o • • o • • o •
• • • • o o ¤ • • ¤ o * o o ¤ o * o • o o o * o o o o o
• • • • • • o • • • • • • o • • • • • • o • • • • • o o
• • • o * o o • • • o • o o • • • o • o o • ¤ o o o o o
• • o • • o • • o • • o
• • • • • • • • • • • •
C-K p-F A-C-K M-g-i
• • o • • o • • o • • o
• o • • o • • o • • o •
o • o o o o o o • o o o o o o • o o o o o o o * o o o o
• • • • • o o • • ¤ • • o o • • o • • o o o • o • • o o
• o * o o o o • o o o o o o • o * o o o o ¤ o • o o o o
o • o * • o o • o o • o
¤ • • o • • o o ¤ o o o
a-c-k-I d-p-F-D-P-p o-x
¤ o o o o o o o o
• o o ¤ o o o o o
o o • o o o o o o o o o o o o o o o o o o
o • o • o o o o • * o o o o o ¤ o * o o o
o o • o * o o o o o o o o o o o o o o o o
o • o o o o o o o
o o o o o o o o o
Порядок некоторых ходов можно менять. Заметьте, что если использовать * для обозначения отверстий, а o для обозначения колышков, вы можете получить решение головоломки, проследуя решение в обратном порядке, начав с последней картинки и двигаясь к первой. Однако это потребует более 18 ходов. |
Решение было найдено в 1912 году Эрнестом Бергхольтом (Ernest Bergholt) и было доказано, что решение кратчайшее Джоном Бисли (John Beasley) в 1964[2].
Это же решение можно видеть на сайте[3], где также вводится нотация Вольстенхолма, которая разработана, чтобы сделать запоминание решения проще.
Другие решения включены в следующий список. Список имеет формат
- Начальная позиция: конечная позиция=
Далее идут пары: колышек и позиция, на которую он переходит. Пары разделены запятой или косой чертой (косая ставится как завершение группы ходов)
x:x=ex,lj,ck,Pf,DP,GI,JH,mG,GI,ik,gi,LJ,JH,Hl,lj,jh,CK,pF,AC,CK,Mg,gi,ac,ck,kI,dp,pF,FD,DP,Pp,ox x:x=ex,lj,xe/hj,Ki,jh/ai,ca,fd,hj,ai,jh/MK,gM,hL,Fp,MK,pF/CK,DF,AC,JL,CK,LJ/PD,GI,mG,JH,GI,DP/Ox j:j=lj,Ik,jl/hj,Ki,jh/mk,Gm,Hl,fP,mk,Pf/ai,ca,fd,hj,ai,jh/MK,gM,hL,Fp,MK,pF/CK,DF,AC,JL,CK,LJ/Jj i:i=ki,Jj,ik/lj,Ik,jl/AI,FD,CA,HJ,AI,JH/mk,Hl,Gm,fP,mk,Pf/ai,ca,fd,hj,ai,jh/gi,Mg,Lh,pd,gi,dp/Ki e:e=xe/lj,Ik,jl/ck,ac,df,lj,ck,jl/GI,lH,mG,DP,GI,PD/AI,FD,CA,JH,AI,HJ/pF,MK,gM,JL,MK,Fp/hj,ox,xe d:d=fd,xe,df/lj,ck,ac,Pf,ck,jl/DP,KI,PD/GI,lH,mG,DP,GI,PD/CK,DF,AC,LJ,CK,JL/MK,gM,hL,pF,MK,Fp/pd b:b=jb,lj/ck,ac,Pf,ck/DP,GI,mG,JH,GI,PD/LJ,CK,JL/MK,gM,hL,pF,MK,Fp/xo,dp,ox/xe/AI/BJ,JH,Hl,lj,jb b:x=jb,lj/ck,ac,Pf,ck/DP,GI,mG,JH,GI,PD/LJ,CK,JL/MK,gM,hL,pF,MK,Fp/xo,dp,ox/xe/AI/BJ,JH,Hl,lj,ex a:a=ca,jb,ac/lj,ck,jl/Ik,pP,KI,lj,Ik,jl/GI,lH,mG,DP,GI,PD/CK,DF,AC,LJ,CK,JL/dp,gi,pd,Mg,Lh,gi/ia a:p=ca,jb,ac/lj,ck,jl/Ik,pP,KI,lj,Ik,jl/GI,lH,mG,DP,GI,PD/CK,DF,AC,LJ,CK,JL/dp,gi,pd,Mg,Lh,gi/dp
Атака на стандартную английскую версию солитера
Место, где может закончиться игра — это центр, либо одна из середин рёбер, и последним ходом мы должны там оказаться.
Ниже приведена таблица числа Возможных Позиций после n ходов, и число Отсутствия Ходов, позиций, в которых продолжение невозможно.
Если позиция может быть получена поворотом либо зеркальным отражением, она считается идентичной.
|
|
|
|
Поскольку максимальное число позиций на каждый ход не превосходит 3626632, а число ходов равно 31, современные компьютеры без труда могут просчитать все позиции за приемлемое время.
Приведённые выше последовательности «ВП» занесены в OEIS под номером A112737[4]. Заметьте, что общее число достижимых позиций (сумма последовательности) равно 23 475 688[4], в то время как общее число возможных позиций равно 233, или, примерно, 233/8 ~ 1 миллиард, если учитывать симметрию. Таким образом, только около 2,2 % всех возможных позиций на доске достижимы, если начинать с пустого центра.
Можно получить все возможные позиции на доске. Результаты, приведённые в таблице, можно получить, используя mcrl2 toolset (смотрите peg_solitaire пример в пакете).
|
|
|
|
Решения для европейского варианта игры
существует 3 начальных неконгруэнтных позиции, имеющие решения. Это:
1)
0 1 2 3 4 5 6
0 o • •
1 • • • • •
2 • • • • • • •
3 • • • • • • •
4 • • • • • • •
5 • • • • •
6 • • •
Возможное решение: [2:2-0:2, 2:0-2:2, 1:4-1:2, 3:4-1:4, 3:2-3:4, 2:3-2:1, 5:3-3:3, 3:0-3:2, 5:1-3:1, 4:5-4:3, 5:5-5:3, 0:4-2:4, 2:1-4:1, 2:4-4:4, 5:2-5:4, 3:6-3:4, 1:1-1:3, 2:6-2:4, 0:3-2:3, 3:2-5:2, 3:4-3:2, 6:2-4:2, 3:2-5:2, 4:0-4:2, 4:3-4:1, 6:4-6:2, 6:2-4:2, 4:1-4:3, 4:3-4:5, 4:6-4:4, 5:4-3:4, 3:4-1:4, 1:5-1:3, 2:3-0:3, 0:2-0:4]
2)
0 1 2 3 4 5 6
0 • • •
1 • • o • •
2 • • • • • • •
3 • • • • • • •
4 • • • • • • •
5 • • • • •
6 • • •
Возможное решение: [1:1-1:3, 3:2-1:2, 3:4-3:2, 1:4-3:4, 5:3-3:3, 4:1-4:3, 2:1-4:1, 2:6-2:4, 4:4-4:2, 3:4-1:4, 3:2-3:4, 5:1-3:1, 4:6-2:6, 3:0-3:2, 4:5-2:5, 0:2-2:2, 2:6-2:4, 6:4-4:4, 3:4-5:4, 2:3-2:1, 2:0-2:2, 1:4-3:4, 5:5-5:3, 6:3-4:3, 4:3-4:1, 6:2-4:2, 3:2-5:2, 4:0-4:2, 5:2-3:2, 3:2-1:2, 1:2-1:4, 0:4-2:4, 3:4-1:4, 1:5-1:3, 0:3-2:3]
и 3)
0 1 2 3 4 5 6
0 • • •
1 • • • • •
2 • • • o • • •
3 • • • • • • •
4 • • • • • • •
5 • • • • •
6 • • •
Возможное решение: [2:1-2:3, 0:2-2:2, 4:1-2:1, 4:3-4:1, 2:3-4:3, 1:4-1:2, 2:1-2:3, 0:4-0:2, 4:4-4:2, 3:4-1:4, 6:3-4:3, 1:1-1:3, 4:6-4:4, 5:1-3:1, 2:6-2:4, 1:4-1:2, 0:2-2:2, 3:6-3:4, 4:3-4:1, 6:2-4:2, 2:3-2:1, 4:1-4:3, 5:5-5:3, 2:0-2:2, 2:2-4:2, 3:4-5:4, 4:3-4:1, 3:0-3:2, 6:4-4:4, 4:0-4:2, 3:2-5:2, 5:2-5:4, 5:4-3:4, 3:4-1:4, 1:5-1:3]
Варианты досок
Солитер играется и на других досках, хотя приведённые две наиболее популярны. Доска может быть треугольной, с ходами в трёх направлениях.
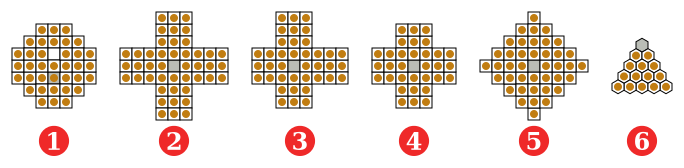
(1) Французская (Европейская), 37 отверстий, 17-й век;
(2) Виглеб (Wiegleb) 1779, Германия, 45 отверстий;
(3) Несимметричная доска 3-3-2-2, как описано Джорджем Беллом (George Bell), 20-й век;
(4) Английская (стандартная), 33 отверстия;
(5) Алмаз, 41 отверстие;
(6) Треугольник, 15 отверстий.
Серое поле = где должен оказаться оставшийся последним колышек.
Обычно треугольный вариант имеет пять отверстий на стороне. Решение, при котором конечный колышек оказывается в начально пустом поле, невозможно в трёх центральных точках. Задача с пустым полем в углу можно решить за десять ходов, если же пустое поле расположено в центре стороны, можно решить за девять ходов (Bell 2008):
| Кратчайшее решение треугольного варианта |
|---|
|
* = колышек, который делает следующий ход; ¤ = отверстие, освободившееся в результате хода; o = удалённые колышки (через которые перепрыгнули); * = отверстие, в котором оказался колышек после хода; • • • * ¤ • • • • • • • * o ¤ • • • • • • * • • ¤ • • * o • • • • • • • • • • • • • • o • • * * • * * • o • • ¤ o * * • o * o ¤ • o • * o • o • • o • o o o o o * * * * ¤ ¤ o o o o o o o o * * o o o o o * o o ¤ ¤ • • ¤ o o o o o o * * o o • o o o o o o * * o • o ¤ ¤ o • o o o o * o o o o ¤ o o * o o |
См. также
Примечания
- ↑ Mathematics and brainvita
- ↑ Смотрите доказательство Бисли в Winning Ways for your Mathematical Plays, том 4 (второе издание).
- ↑ Описание решения
- 1 2 Последовательность A112737 в OEIS = On the standard 33-hole cross-shaped peg solitaire board, the number of distinct board positions after n jumps (starting with the center vacant)
Литература
- D. Avis, A. Deza. On the solitaire cone and its relationship to multi-commodity flows // Mathematical Programming. — 2001. — Т. 90, вып. 1. — С. 27–57. — DOI:10.1007/PL00011419..
- John D. Beasley. The Ins & Outs of Peg Solitaire. — Oxford University Press, 1985. — ISBN 978-0198532033.
- G. I. Bell. Solving triangular peg solitaire // Journal of Integer Sequences. — 2008. — Т. 11. — С. Article 08.4.8. — arXiv:math.CO/0703865..
- E. R. Berlekamp, J. H. Conway, R. K. Guy. Winning Ways for your Mathematical Plays. — London: Academic Press, 1982..
- N. G. de Bruijn. A solitaire game and its relation to a finite field // Journal of Recreational Mathematics. — 1972. — Т. 5. — С. 133–137..
- D. C. Cross. Square solitaire and variations // Journal of Recreational Mathematics. — 1968. — Т. 1. — С. 121–123..
- M. Gardner. Mathematical games // Scientific American. 206 (6): 156—166, June 1962; 214 (2): 112—113, Feb. 1966; 214 (5): 127, May 1966.
- M. Kiyomi, T. Matsui. Proc. 2nd Int. Conf. Computers and Games (CG 2000). — 2001. — Т. 2063. — С. 229–240. — (Lecture Notes in Computer Science). — DOI:10.1007/3-540-45579-5_15..
- R. Uehara, S. Iwata. Generalized Hi-Q is NP-complete // Trans. IEICE. — 1990. — Т. 73. — С. 270–273..
Ссылки
- HTML5 версия Albino Tonnina
- Игра Солитер и её связь с конечными полями
- Игра Солитер и теория групп
- George I. Bell. Peg Solitaire.
- Jaap Scherphuis. Analysis of Peg Solitaire. Jaap's Puzzle Page.
- Солитер на прямоугольной доске 12 F3
- Классические доски игры Солитер F1
- Игра Солитер на доске 16 F2
- Игра Солитер на доске 25 F2
- Солитер Пошаговое решение английской версии игры Солитер
Для улучшения этой статьи желательно: |
Данная страница на сайте WikiSort.ru содержит текст со страницы сайта "Википедия".
Если Вы хотите её отредактировать, то можете сделать это на странице редактирования в Википедии.
Если сделанные Вами правки не будут кем-нибудь удалены, то через несколько дней они появятся на сайте WikiSort.ru .

