WikiSort.ru - Не сортированное

Снарки Блануши
Назван в честь	Данило Блануши
Вершин	18 (оба)
Рёбер	27 (оба)
Диаметр	4 (оба)
Обхват	5 (оба)
Автоморфизмы	8, D4 (1-й) 4, группа Клейна (2-й)
Хроматическое число	3 (оба)
Хроматический индекс	4 (оба)
Свойства	снарк (оба) гипогамильтонов (оба) кубический (оба) тороидальный (только один)[1]

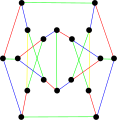
Снарк Блануши — 3-регулярный граф с 18 вершинами и 27 рёбрами^[2]. Существуют два таких графа. Носят имя нашедшего оба этих графа в 1946 году югославского математика Данило Блануши^[3]. (На момент 1946 года был известен всего один снарк — граф Петерсена.)

Как и все снарки, снарки Блануши являются связными кубическими графами без мостов с хроматическим индексом 4. Оба имеют хроматическое число 3, диаметр 4 и обхват 5. Они негамильтоновы, но гипогамильтоновы^[4].

Алгебраические свойства

Группа автоморфизмов первого снарка Блануши имеет порядок 8 и изоморфна диэдрической группе ${\displaystyle D_{4}}$  — группе симметрии квадрата.

Группа автоморфизмов второго снарка Блануши является абелевой группой порядка 4 и изоморфна четверной группе Клейна — прямому произведению циклической группы ${\displaystyle \mathbb {Z} /2\mathbb {Z} }$ на себя.

Характеристические многочлены первого и второго снарков Блануши:

${\displaystyle (x-3)(x-1)^{3}(x+1)(x+2)(x^{4}+x^{3}-7x^{2}-5x+6)(x^{4}+x^{3}-5x^{2}-3x+4)^{2}\ }$ ,

${\displaystyle (x-3)(x-1)^{3}(x^{3}+2x^{2}-3x-5)(x^{3}+2x^{2}-x-1)(x^{4}+x^{3}-7x^{2}-6x+7)(x^{4}+x^{3}-5x^{2}-4x+3)}$ .

Обобщённые снарки Блануши

Существуют обобщения первого и второго снарков Блануши до двух бесконечных семейств снарков порядка ${\displaystyle 8n+10}$ , которые обозначаются ${\displaystyle B_{n}^{1}}$ и ${\displaystyle B_{n}^{2}}$ . Снарки Блануши являются наименьшими членами этих двух семейств^[5].

В 2007 Мазак (J. Mazak) доказал, что цикловой хроматический индекс обобщённых снарков Блануши ${\displaystyle B_{n}^{1}}$ равен ${\displaystyle 3+{\frac {2}{n}}}$ ^[6].

В 2008 Геблех (M. Ghebleh) доказал, что цикловой хроматический индекс обобщённых снарков Блануши ${\displaystyle B_{n}^{2}}$ равен ${\displaystyle 3+{\frac {1}{\lfloor 1+3n/2\rfloor }}}$ ^[7].

Галерея

• 
  хроматическое число первого снарка Блануши равно 3.
• 
  хроматический индекс первого снарка Блануши равен 4.
• 
  хроматическое число второго снарка Блануши равно 3.
• 
  хроматический индекс второго снарка Блануши равен 4.

Примечания

Для улучшения этой статьи желательно: Проверить качество перевода с иностранного языка. Исправить статью согласно стилистическим правилам Википедии.