Парадокс Линдли — это контринтуитивная ситуация в статистике, при которой байесовский и частотный[en] подходы к задаче проверки гипотез дают различные результаты при определённых выборах априорного распределения. Проблема разногласия между двумя подходами обсуждалась в книге Гарольда Джеффриса 1939 года[1]. Проблема стала известна как парадокс Линдли после того, как Деннис Линдли высказал несогласие с парадоксом в статье 1957[2].
Хотя ситуация описывается как парадокс, различие байесовского и частотного подходов можно объяснить как использования их для ответа на фундаментально различные вопросы, а не действительного разногласия между двумя методами.
Как бы то ни было, для большого класса априорные разности между частотным и байесовским подходами вызваны сохранением уровня значимости. Как Линдли понял, «теория не может обосновать практику сохранения уровня значимости» и даже «некоторые вычисления, сделанные профессором Пирсоном в обсуждении этой статьи подчёркивают, насколько уровень значимости может меняться с изменением размера выборки, если потери и априорные вероятности остаются неизменными»[2]. Фактически, если критичное значение растёт с ростом размера выборки достаточно быстро, рассогласование между частотным и байесовским подходами становится ничтожным[3][4].
Описание парадокса
Рассмотрим результат некоторого эксперимента с двумя возможными объяснениями, гипотезами и , и некоторым априорным распределением , представляющим неопределённость, какая гипотеза более точна перед рассмотрением .
Парадокс Линдли обнаруживается в случае
- Результат оказывается «значимым» для частотного теста гипотезы , показывающим значимое свидетельство к отбрасыванию гипотезы , скажем, на уровне 5%
- Апостериорная вероятность гипотезы , задаваемая результатом высока, что убедительно свидетельствует о том, что гипотеза больше согласуется с , чем гипотеза .
Эти результаты могут случиться в одно и то же время, если очень специфично, более размыто, а априорное распределение не даёт предпочтения ни одному из них, как показано ниже.
Численный пример
Мы можем проиллюстрировать парадокс Линдли численным примером. Представим себе город, в котором родились 49581 мальчиков и 48870 девочек за определённый период времени. Наблюдаемая доля мальчиков составляет 49581/98451 ≈ 0,5036. Мы предполагаем, что число рождений мальчиков является биномиальной переменной с параметром . Мы хотим проверить, равно ли 0,5 или другому значению. То есть, наша нулевая гипотеза гласит: , а альтернативной гипотезой будет .
Частотный подход
Частотный подход проверки заключается в вычислении p-значения, вероятности наблюдения доли мальчиков не менее в предположении, что гипотеза верна. Поскольку число рождений большое, мы можем использовать нормальную аппроксимацию для доли рождения мальчиков , с и для вычисления
Мы также будем удивлены, если рассмотрим рождение 48870 девочек, то есть, , так что частотный тест обычно осуществаляет двухстороннюю проверку, для которой p-значение было бы . В обоих случаях p-значение меньше уровня значимости в 5%, так что частотный подход отвергает гипотезу как несогласующуюся с наблюдаемыми данными.
Байесовский подход
Предполагая, что нет причин для предпочтения одной гипотезы другой, байесовский подход заключается в назначении априорных вероятностей , однородного распределения для для гипотезы и, затем, вычисления апостериорной вероятности для с помощью теоремы Байеса,
После наблюдения рождения мальчиков из новорождённых, мы можем вычислить апостериорную вероятность каждой гипотезы с помощью функции распределения масс для биномиальной переменной,
где является бета-функцией.
Из этих значений мы находим апостериорную вероятность , которая строго предпочитает перед .
Два подхода, частотный и байесовский, оказываются в конфликте, а это и есть «парадокс».
Примирение байесовского и частотного подходов
Однако, по меньшей мере, в примере Линдли, если мы возьмём последовательность уровней значимости , таких что с , то апостериорная вероятность нулевой гипотезы стремится к 0, что согласуется с отказом от нулевой гипотезы[3]. В нашем числовом примере, если принять , в результате получим уровень значимости 0,00318, так что частотный подход не будет отбрасывать нулевую гипотезу, которая в общих чертах согласуется с байесовским подходом.
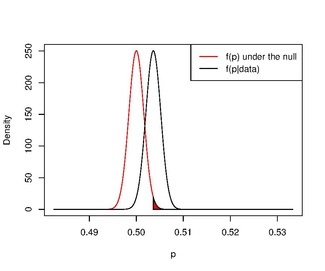
Если используется информативное априорное распределение и проверка гипотезы, более похожей на гипотезу в частотном подходе, парадокс исчезает.
Например, если мы вычисляем апостериорное распределение , используя однородное априорное распределение с (то есть, ), мы получим
Если мы используем это для проверки вероятности, что новорождённый более вероятно будет мальчиком, чем девочкой, то есть, , мы получим:
Другими словами, очень похоже, что пропорция рождения мальчиков выше 0,5.
Ни один из анализов не даёт оценку величины эффекта[en] прямо, но оба могут быть использованы для определения, например, является ли доля рождений мальчиков выше некоторого определённого порога.
Отсутствие действительного парадокса
Явное расхождение между двумя подходами вызвано комбинацией факторов. Во-первых, частотный подход проверяет выше без учёта . Байесовский подход вычисляет как альтернативу к и находит, что первая гипотеза больше согласуется с наблюдениями. Это потому, что последняя гипотеза существенно более размыта, так как значение может быть любым в интервале , что приводит к очень низкой апостериорной вероятности. Чтобы понять почему, полезно рассмотреть две гипотезы как генераторы наблюдений:
- В гипотезе мы выбираем и задаём вопрос, насколько правдоподобно видеть 49581 мальчиков при 98451 новорождённых.
- В гипотезе мы выбираем случайно между 0 и 1 и задаём тот же вопрос.
Большинство возможных значений для при гипотезе очень плохо поддерживаются наблюдениями. По существу, явное несогласие между методами вообще не является несогласием, а являются двумя различными утверждениями относительно данных:
- Частотный подход находит, что плохо объясняется наблюдениями.
- Байесовский подход находит, что гипотеза существенно лучше объясняется наблюдениями, чем гипотеза .
Отношение пола новорождённых в 50/50 (мальчиков/девочек) согласно частотному тесту неправдоподобно. Всё же, отношение 50/50 является лучшим приближением чем большинство, но не все другие отношения. Гипотеза подходила бы наблюдениям много лучше, чем все другие отношения, включая .
Например[5], из этого выбора гипотезы и априорной вероятности следует утверждение: «Если
> 0,49 и
< 0,51, то априорная вероятность
быть ровно 0,5 равна 0,50/0,51
98%». Если дано такое сильное предпочтение для
, легко видеть, что байесовский подход высказывается в пользу
, учитывая что
, даже когда наблюдаемое значение
лежит в
от 0,5. Отклонение более
от
считается значимым в частотном подходе, но значимость отклоняется априорной вероятностью в байесовском подходе.
Если смотреть в другую сторону, мы можем видеть, что априорное распределение существенно плоским с дельта функцией в точке . Ясно, что является сомнительным. Фактически, если вы попробуете нарисовать вещественные числа как непрерывные, будет логично предположить, что невозможно для заданного параметра .
Более реалистичное распределение для на альтернативной гипотезе даёт менее удивительные результаты для апостериорной вероятности гипотезы . Например, если мы заменим на , то есть, оценку максимального правдоподобия для , апостериорная вероятность гипотезы будет только 0,07 по сравнению с 0,93 для гипотезы (конечно, нельзя использовать в действительности оценку максимального правдоподобия как часть априорного распределения).
Современное обсуждение
См. также
Примечания
- ↑ Jeffreys, 1939.
- 1 2 Lindley, 1957, с. 187–192.
- 1 2 3 Spanos, 2013, с. 73–93.
- ↑ Naaman, 2016, с. 1526–1550.
- ↑ Данный раздел в английской версии подвергается критике как требующий полной переработки.
- ↑ Sprenger, 2013, с. 733–744.
- ↑ Robert, 2014.
Литература
- Glenn Shafer. Lindley's paradox // Journal of the American Statistical Association. — 1982. — Т. 77, вып. 378. — С. 325–334. — DOI:10.2307/2287244.
- Harold Jeffreys. Theory of Probability. — Oxford University Press, 1939.
- Lindley D.V. A Statistical Paradox // Biometrika. — 1957. — Т. 44, вып. 1–2. — DOI:10.1093/biomet/44.1-2.187.
- Michael Naaman. Almost sure hypothesis testing and a resolution of the Jeffreys-Lindley paradox // Electronic Journal of Statistics. — 2016. — Т. 10, вып. 1. — ISSN 1935-7524. — DOI:10.1214/16-EJS1146.
- Aris Spanos. Who should be afraid of the Jeffreys-Lindley paradox? // Philosophy of Science. — 2013. — Т. 80.1. — DOI:10.1086/668875.
- Jan Sprenger. Testing a Precise Null Hypothesis: The Case of Lindley's Paradox // Philosophy of Science. — 2013. — Т. 80. — DOI:10.1086/673730.
- Christian P. Robert. On the Jeffreys-Lindley Paradox // Philosophy of Science. — 2014. — Т. 81.2. — DOI:10.1086/675729. — arXiv:1303.5973.
Для улучшения этой статьи желательно: |
Данная страница на сайте WikiSort.ru содержит текст со страницы сайта "Википедия".
Если Вы хотите её отредактировать, то можете сделать это на странице редактирования в Википедии.
Если сделанные Вами правки не будут кем-нибудь удалены, то через несколько дней они появятся на сайте WikiSort.ru .

























![{\displaystyle \pi (\theta \in [0,1])=1}](https://wikimedia.org/api/rest_v1/media/math/render/svg/501cfa93f3445e054a5b1a8de6830449f0bdbce8)



![{\displaystyle [0,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/738f7d23bb2d9642bab520020873cccbef49768d)









